Semi active damping of the car

21. Marec, 2011, Autor článku: Vondřich Jiří, Elektrotechnika
Ročník 4, číslo 3 This page as PDF Pridať príspevok

The model of the car consists of a stiff chassis, front and rear axles, springs, dampers and wheel disks with tires. The vehicle wheels running on uneven road. Semi active systems can only change the viscous damping coefficient of the damper, and do not add energy to the suspension system.

Though limited in their intervention, semi active suspensions are less expensive to design and consume far less energy. In recent times, research in semi-active suspensions has continued to advance with respect to their capabilities, narrowing the gap between semi active and fully active suspension systems.

1. System model

Model vehicles running on uneven roads is shown in Fig. 1


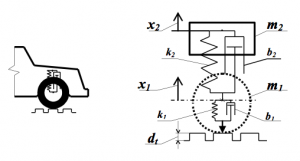
Figure 1: Scheme and model of automobile wheel moved on the rough road

The equations of motion of the model are

m_2 \ddot{x_2} = (x_1 - x_2)k2 + (\dot{x_1} - \dot{x_2})b_2 (1)

m_1 \ddot{x_1} = -(x_1 - x_2)k2 - (\dot{x_1} - \dot{x_2})b_2 + (d_t - x_1)k_1 + (\dot{d_t} - \dot{x_1})b_1 (2)

The SIMULINK scheme of the model is in Fig.2.


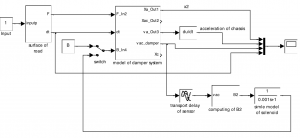
Figure 2: SIMULINK scheme of the model of the complete system


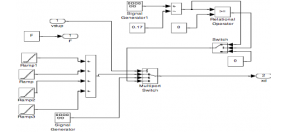
Figure 3: SIMULINK scheme of the surfaces of roadway

The SIMULINK scheme of the model of wheel and chassis parallel interlinked with damper and spring is in Fig.4.


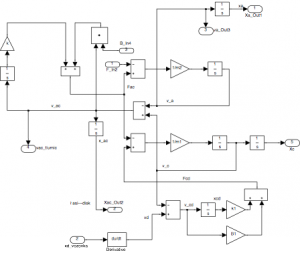
Figure 4: Model of wheel and chassis parallel of interlinked with damper and spring

2. Model of the controller

The parameter of damping constant moves between two parameters b2 and b2min. The damper on the chassis power inductive of acceleration of the chassis size of A, which is (g) is concluded by the passive damping. If the acceleration is A=0, the damping is constant maximal, b2. By the size of the acceleration A=1, it is g=9,81 ms-2 is the damping constant b2= b2min. The damping constant has between this interval linear proportional dependence. If is A>g, damping constant b2= b2min.

The SIMULINK scheme of the controller of the damping constant b2 is in Fig.5.


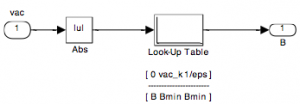
Figure 5: SIMULINK scheme of the controller of the damping constant b2

3. Results

In the Fig.6 and Fig.7 dependences of the deviation and acceleration of the chassis on the time for alternative passive and semi active damping and moving the wheel on the square-wave pulse are shown.


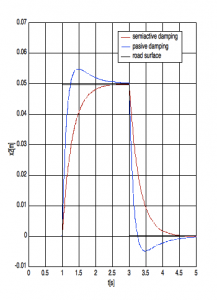
Figure 6: Time dependence deviation of chassis (square wave-pulse)


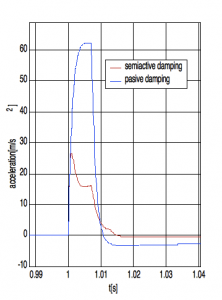
Figure 7: Time dependence acceleration of chassis (square wave-pulse)

In the Fig.8 and Fig.9 dependences of the deviation and acceleration of the chassis on the time for alternative passive and semi active damping and moving the wheel on positive part of sine wave is shown.


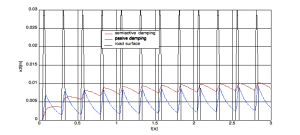
Figure 8: Time dependence deviation of the chassis (positive part of sine wave)


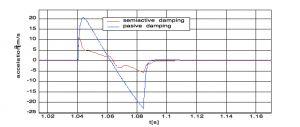
Figure 9: Detail of time dependence acceleration of chassis (positive part of sine wave)

4. Conclusion

At the semi active damping the amplitude of oscillation is smaller as at the passive damping. The results depend on the exactness of numerical solution. This exactness is possible to set up in SIMULINK on card Simulation-Parameters-Solver.

The semi active suspension system consists of a spring, where the shock is equipped with a control unit to automatically adjust damping coefficient. Unlike active suspension does not power generator power and the suspension is semi active cheaper than active. Proceedings semi active suspension of their cars is used to reduce the dynamic forces at the tire caused by random road bumps. For semi active control is only remove power. This eliminates the risk of destabilization in many cases it is possible to achieve better results than a purely passive solutions.

References

  1. J. P. Den Hartog. Mechanical Vibrations. Mc GuAW Company, New Your, 1947.

Napísať príspevok