Vibration suppression of two-dimensional systems with optimal distribution of sensors and actuators

13. Júl, 2011, Autor článku: Benkovský Peter, Elektrotechnika
Ročník 4, číslo 7 Pridať príspevok

This paper deals with the development of process for finding the optimal number and location of piezoceramic actuators and sensors to suppress the vibration of 2D systems. This choice must satisfy the condition of maximum possible system observability and controllability and is independent of the choice of control algorithm.

Controllability and observability of the system is expressed via grammians of controllability and observability, respectively as product of these two items. The problem is solved by the optimization process in MATLAB program using a combination of library functions as well as its own created function and a set of input data from system model from program package ANSYS. Comparing the matrix product of grammians in the optimization process, serves as the main benchmark and its result is a set of indicia location of piezoceramic members.

1. Introduction

The aim of this work is to take advantage of already known theoretical principles (Halim D. and Moheimani, 2003; Gawronsky W.K, 2004) to solve more general issues, namely, the systems with non-constant thickness, complex boundary conditions, etc. The main objective is to design optimization algorithm and subroutine that will process the input data. Maximization of observability and controllability grammians was chosen as main condition for this optimization problem.

Calculation of grammians can be realized in state-space balanced representation, which guarantees that observability and controllability grammians will be diagonal and the same. Finally, solving the optimization problem for selected modes will return node indexes, if they satisfy the criteria adopted.

1.1 Secondary Heading

Alongside with the solving of the main problem it was necessary to deal with data repairing. This was critical in matrix/model reconstruction after importing model from ANSYS to MATLAB. Since conventional data import could not be used, data transfer was realized by set of subroutines, which provided all necessary information like mass, stiffness matrix, geometry, indexing of nodes and so on. These subroutines were also solving the problem of mixed or missing nodes due matrix reduction.

Fig. 1 Clamped beam in node 1

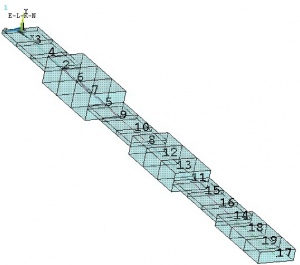
For illustration we have clamped beam with mixed nodes as it is shown in Figure 1. Figure 2 represents first mode of beam right after importing model from ASNYS to MATLAB.

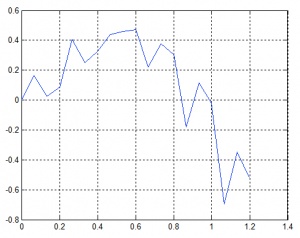
Fig. 2 Mixed/wrong mode of beam

After that we will sort results based on information from imported data.

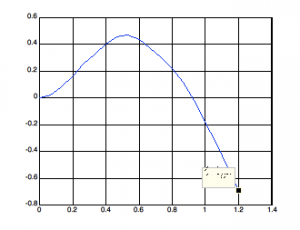
Fig. 3 Repaired/ sorted mode of same beam

2. Preliminaries and problem formulation

In general, we obtain nodal model from FEM, which will be implemented into our MATLAB solver:

$M \ddot{q} + Kq =0$

(1)

It’s a system without inputs and outputs with nd degrees of freedom. M, K are mass and stiffness matrices with dimensions (n_d x n_d). q and their second derivatives are displacement vector and acceleration vector with dimensions (n_d x 1). Using prescribed subroutines we will transform this system to state space and at the same time we will create inputs and outputs of the system (Gawronsky 2004).

$x = \left \{ \begin{array}{c} x_1 \\ x_2 \end{array} \right \} = \left \{ \begin{array}{c} q \\ \dot{q} \end{array} \right \}$

$\dot{x_1}=x_2$

$\dot{x_2} = M^{-1}Kx_1+M^{-1}B_0u$

$y=C_{oq}x_1+C_{ov}x_2$

(2)

Where x is state vector and a B₀, C_oq, C_ov are input matrix, output displacement and velocity matrices in a nodal form. Their dimensions are (2*n_d x 1), (n_d x s), (r x n_d) a (r x n_d), where s and r represent the number of inputs and outputs of the system. Now we can calculate observability and controllability grammians Wo and Wc using Lyapunov equation:

$AW+WA^T +BB^T=0$

$A^TW_o+W_oA+C^TC=0$

(3)

Using information about balanced representation we can obtain both grammians that will be diagonal and equal (Starek, 2009, Moore 1981):

$W_o=W_c=\Gamma$

$\Gamma = diag(\gamma_1, \dots , \gamma_{2n})$

$\gamma_i \geq 0, \quad i=1,\dots,2n$

(4)

So now we can define grammians as functions of i-th location of inputs and outputs on structure and the degree of observability and controllability for each mode (or mode m) by:

$\Gamma_m = f_m(i)$

(5)

$M_m=\frac{\Gamma_m(i)}{max(\Gamma_m)} . 100\%$

(6)

Similarly we can define the degree of observability and controllability on the whole structure for all selected modes,

$S=\frac{\sum Q_m \Gamma_m(i)}{max \sum(\Gamma_m)} . 100\%$

(7)

as summation of functions $\Gamma_m$ of selected modes in i-th location, divided by maximum of this summarized functions. Where $Q_m$ is weighting function for each mode (inspired by Halim and Moheimani 2003).

3. Main results

Result of this work will be algorithm which will find optimal placement for sensors and actuators placed on virtual FEM model imported from ANSYS. Optimization is based on modal and spatial observability and controllability. Equation (6) and (7) are modified versions of modal and spatial observability and controllability from (Halim and Moheimani 2003). They are functions of “i” which is number mode directly.

4. Example

Let’s have thin squared plate of these attributes:

Dimension: 1 x 1 meter
Thickness: 0.01 meter
Material – Aluminum
Density: 2700 kg/m³
Young modulus: 70 GPa

First three natural frequencies for transverse vibration in ANSYS are:

17.828 Hz
38.883 Hz (2 symmetric modes)
48.261 Hz

Pinned at nodes: 1, 2, 12, and 22.

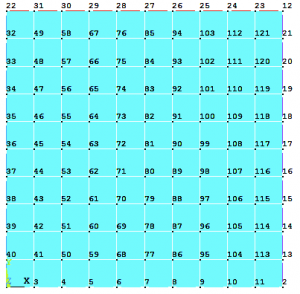
Fig. 3 Plate with map of nodes

Task is to find optimal placement of collocated sensors and actuators for 1^st, 2^nd and 4^th mode with different number of collocated patches.

Plate has 121 nodes and with standard ANSYS node counting they are mixed up. Also ANSYS will reduce all nodes with zero DOF and rest of them (117 nodes) will be mixes up even further. It is necessary to find the sorting indices right after we read attributes of the plate to MATLAB Without sorting indices the inputs and outputs will be misplaced and all calculations with model will be completely wrong.

Next stage of solving the problem is calculation of observability and controllability map of the system for selected modes by using Lyapunov equation also included in MATLAB. We used collocated actuators and sensors on the plate so we will use same sorted input-output index “i”. Applying equations (6) and (7) we will get pointer to vector of node positions, but still remember that equations of system were shuffled by ANSYS twice. Again we need to apply sorting indices on pointer to get right node position.

Table 1 Node numbers in dependence of mode and quantity of inputs/outputs

Number of S/A	Mode 1	Mode 2	Mode 4
1	[81]	-	-
2	[72 81]	[45 117] [7 27]	-
4	[72 80 82 90]	[6 8 26 28]	[7 17 36 27]

5. Conclusion

The algorithm is working quite well for independent modes, but needs proper weighting function when it is solving a set of modes. Also, with too many combinations, computational time is increasing significantly, which can be remedied by optimizing subroutine for input/output combinations generation. Algorithm was also tested on beam structure with variable thickness over its length, with similar properties. Patches are considered as points located at a node, which affects the accuracy.

Acknowledgments

The authors gratefully acknowledge the support of the Slovak Ministry of Education Grant Agency VEGA # 1/0744/10.

References

Gawronsky W.K, 2004, Advanced structural dynamics and active control of structures, Mechanical engineering series, Springer Verlag New York Inc.
Halim D and Moheimani S O R 2003 An optimization approach to optimal placement of collocated piezoelectric actuators and sensors on a thin plate, Mechatronics 13 27–47
Moor, B.C, Principal Component Analysis in Lienear Systems, Controllability, Observability and Model Reduction, IEEE Transactions on Automatic Control, vol. 26, 1981, pp. 17-32
Starek L. 2009, Kmitanie s riadením , Vydala Slovenská technická univerzita v BA v Nakladateľstve STU , Edícia vysokoškolských učebníc, ISBN 978-80-227-3227-7.

Coauthor of this paper is L. Starek, Institute applied mechanics and mechatronics, Slovak Technical University in Bratislava

O časopise

Meta

RSS

Vibration suppression of two-dimensional systems with optimal distribution of sensors and actuators

Napísať príspevok

Rubriky

Burza práce

Štúdijné materiály

Archív