Výpočet obecného řídícího zákona prediktivního řízení pro systému druhého řádu bez omezení

29. Júl, 2011, Autor článku: Brázdil Michal, Elektrotechnika
Ročník 4, číslo 7 Pridať príspevok

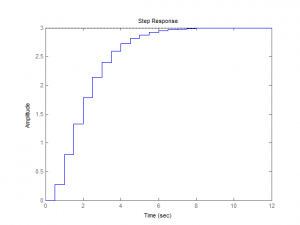
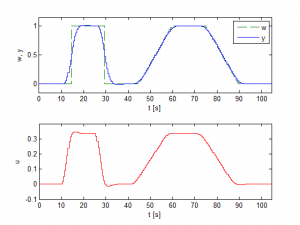
Tento článek se zabývá výpočtem obecného řídicího zákona prediktivního řízení pro systém druhého řádu bez omezení. V první části je stručně popsáno prediktivní řízení, jeho hlavní principy a pojmy. V další části je odvozen obecný řídící zákon prediktivního řízení pro systém druhého řádu bez omezení. Třetí a poslední část je věnována simulačnímu ověření vypočítaného zákona pro konkrétní systém.

Stručný úvod do prediktivního řízení

Prediktivní řízení je jednou z metod návrhů řízení, která si získala v posledních letech velkou popularitu. Prediktivní řízení je ve své podstatě založeno na použití diskrétních modelů procesů, a proto jejich odvození příslušných řídících algoritmů je realizováno hlavně v diskrétní oblasti. Pod pojmem prediktivní řízení chápeme třídu metod řízení, které spojují určité společné charakteristiky:

Matematický model řízení systému je použitý na predikci budoucího řízení výstupu systému.
Průběh trajektorie žádané hodnoty regulované veličiny je znám v budoucím čase.
Výpočet posloupnosti budoucích řídicích zásahů zahrnuje minimalizaci vhodné účelové funkce s budoucími trajektoriemi přírůstků řízení a regulační odchylky.
Pouze první hodnota akčního zásahu je použita a celý postup minimalizace účelové funkce se opakuje v další periodě vzorkovaní.

Jednou z předností prediktivního řízení je možnost uvažovat omezení vstupních a výstupních (případně stavových) veličin přímo do návrhu regulátoru. Algoritmy prediktivního řízení jsou při řízení procesů mnohostranně použitelné a robustní. Kvalita řízení ve srovnání s PID regulátory je vyšší. Tyto regulátory jsou použitelné na neminimálně fázové, nestabilní a mnohorozměrné procesy, ale také na systémy s dopravním zpožděním.

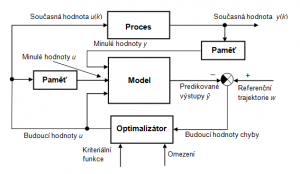
Obr. 1: Základní struktura prediktivního řízení

Základní struktura prediktivního řízení je znázorněna na Obr. 1, jeho princip je uvedený na Obr. 2:

Model řízeného procesu je explicitní částí regulátoru a je používán na predikci N budoucích výstupů procesu $\hat{y}$ . Predikce jsou vypočítané vzhledem k informacím dostupných do času k a vzhledem k neznámé trajektorii akčních zásahů, které je třeba určit.
Trajektorie budoucích akčních zásahů je určena z řešení vhodné účelové funkce a omezení. Účelová funkce zahrnuje budoucí predikce výstupu, budoucí trajektorie žádané veličiny a budoucích akčních zásahů.
I když byla v předešlém kroku počítána celé trajektorie akčních zásahů, pro řízení procesu je použit pouze první člen u(k). V další periodě vzorkování se celý postup opakuje. Tento princip je označován jako strategie pohyblivého horizontu.

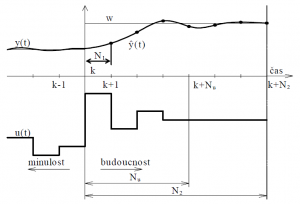
Obr. 2: Princip prediktivního řízení (N₁, N₂, N_u – minimální, maximální, řídící horizont)

Základní rozdělení modelů

V prediktivním řízení je možné použít libovolný model procesu. Vhodný model musí dostatečně vystihovat dynamické vlastnosti procesu. Nejčastěji se používají lineární modely, protože v případě bez omezení je možné vypočítat trajektorii akčních zásahů. Model procesu je potřebný pro výpočet predikce budoucí výstupní trajektorie. Některé modely v sobě přímo zahrnují modely poruch, v jiných se předpokládá, že poruchy jsou konstantní.

Impulzní odezva

Tento model se označuje jako FIR. Výstup je svázaný se vstupem vztahem

$y(k) = \sum_{i=1}^{N} h_i u(k-i) = H(z^{-1}) u(k)$

(1)

Přechodová funkce

Je velmi podobný modelu FIR a je často používaný v průmyslových aplikacích.

$y(k) = \sum_{i=1}^{N} g_i \Delta u(k-i) = G(z^{-1})(1-z^{-1}) u(k)$

(2)

Přenosová funkce

Tento model je použit v metodě GPC (Generalized Predictive Control).

$A(z^{-1}) y(k) = B(z^{-1}) u(k)$

(3)

Stavový popis

$x(k+1) = Ax(k) + Bu(k)$

$y(k) = Cx(k)$

(4)

Poruchy

Nejčastěji používaným popisem poruch je ARMA proces

$n(k) = \frac{C(z^{-1})}{D(z^{-1})} e_s(k)$

(5)

kde e_s je bílý šum. Když uvažujeme model procesu daný rovnicí (3), celkový model může být vyjádřen vztahem ARMAX

$A(z^{-1}) y(k) = B(z^{-1}) u(k) + C(z^{-1}) e_s(k)$

(6)

Účelová funkce

Standardní účelová funkce obsahuje kvadratické členy filtrované regulační odchylky a přírůstků řízení na konečném horizontě do budoucnosti

$J = \sum_{i=N_1}^{N_2} [ P \tilde{y}(k+1) - w(k+i)]^2 + \lambda \sum_{i=1}^{N_u} [ \Delta u(k+i-1)]^2$

(7)

kde $\tilde{y}(k+i)$ je výstup i kroků do budoucnosti predikovaných vzhledem k informacím dostupných do času k , w(k+1) je posloupnost žádané veličiny a $\Delta u(k+i-1)$ je posloupnost budoucích přírůstků řízení, které mají být spočítány. Implicitně se předpokládají omezení na přírůstky řízení ve tvaru:

$\Delta u(k+i-1) = 0, \quad N_u <td style="width:20px; text-align:center;">(8)</td> </tr> </table> Účelová funkce má následující parametry: <ul> <li>Parametry N1, N2 a Nu nazýváme minimální, maximální a řídicí horizont. N1 a N2 určují interval v budoucnosti ke sledování trajektorie žádané hodnoty regulované veličiny. N1 volíme minimálně Td+1 , kde Td je hodnota dopravního zpoždění procesu. Nastavením dostatečné velké hodnoty N1 se můžeme vyhnout problému s neminimálně fázovými procesy. Hodnota N2 by měla pokrývat důležitou část přechodové charakteristiky, obvykle se volí porovnatelná s časem, za kterou výstupní veličina přejde z 10% do 90% své ustálené hodnoty. Řídicí horizont Nu snižuje výpočtovou náročnost</li> <li>Parametry P a <img src='http://s0.wp.com/latex.php?latex&bg=ffffff&fg=000000&s=0' alt='' title='' class='latex' />\lambda$ jsou sekvence, kterými můžeme ovlivňovat budoucí chování řízeného řízeného procesu. Obvykle je volíme jako konstanty nebo ve formě exponenciálních vah.

Důležitým předpokladem je, že trajektorie žádané hodnoty regulované veličiny w(k+1) je známa. V opačném případě se nejčastěji uvažuje konstantní žádaná hodnota rovna aktuální žádané hodnotě.

Cílem prediktivního řízení je spočítat sekvenci budoucích hodnot změny akčního zásahu tak, aby bylo minimalizováno kritérium (7). Výstup modelu lze spočítat jako součet volné odezvy modelu y₀ a nucené odezvy y_n. Volná odezva je závislá pouze na minulých hodnotách řízení a výstupu systému. Nucená odezva bere v potaz nenulové budoucí změny akčního zásahu. Nucenou odezvu lze spočítat jako součin matice G a vektoru budoucích změn akčního zásahu $\tilde{u}$ , kterou obecně dopředu známe

$\tilde{y} = y_n+y_0=G \tilde{u} +y_0$

(9)

Účelovou funkci (7) převedeme do maticové podoby

$J=(G \tilde{u} +y_0 -w)^T (G \tilde{u} +y_0 -w) + \lambda \tilde{u}^T \tilde{u}$

(10)

Dosazením rovnice (9) do rovnice (10) dostáváme

$J=(\tilde{y} -w)^T (\tilde{y} -w) + \lambda \tilde{u}^T \tilde{u}$

(11)

Nyní máme kritérium v maticové podobě, kde $\tilde{y}$ – vektor predikovaných výstupů systému, $\tilde{u}$ – vektor změn akčních zásahů, w – vektor budoucích hodnot žádané veličiny, y₀ – vektor volné odezvy modelu, G – Jacobián modelu, pro kauzální systémy se jedná o trojúhelníkovou matici, pro lineární systém je tvar matice znám. Obsahuje koeficienty odezev modelu na jednotkový skok.

Účelovou funkci (11) převedeme do maticového tvaru používaného pro metody kvadratického programovaní

$J=\frac{1}{2} \tilde{u}^T H \tilde{u} + b^T \tilde{u} +f_0$

(12)

kde

$H=2(G^T G + \lambda I)$

(13)

$b^T = 2 (y_0 -w)^T G$

(14)

$f_0 = (y_0-w)^T (y_0-w)$

(15)

Člen f₀ v rovnici (12) není závislý na $\tilde{u}$ , proto na řešení optimalizační úlohy nemá žádný vliv a z rovnice jej můžeme vypustit. Výsledný tvar kritéria pro optimalizaci

$J=\frac{1}{2} \tilde{u}^T H \tilde{u} + b^T \tilde{u}$

(16)

Omezující podmínky

Velkou výhodou prediktivního řízení je možnost zavést omezení veličin, jako jsou omezení akčního zásahu, omezení výstupní veličiny atd., přímo do návrhu regulátoru. Existují dva druhy omezujících podmínek:

Tvrdé – omezení není možné za žádných okolností překročit
Měkké – omezení je možné překročit s určitou tolerancí

V praxi se používá omezení pomocí saturace. Nevýhodou je, že dochází ke snížení kvality řízení a omezení je možné aplikovat pouze na výstup regulátoru.

Výpočet obecného řídicího zákona

Pro zjednodušení odvození řídicího zákona prediktivního regulátoru byly zanedbány omezující podmínky. V opačném případě by musela být tato úloha řešena pomocí optimalizačních technik. Pro odvození řídicího zákona byl použit CARIMA model, který nejlépe popisuje procesy v průmyslu, který má tvar:

$A(z^{-1}) y(k) = B(z^{-1}) u(k) + \frac{C(z^{-1})}{\Delta} e_s(k)$

(17)

kde $A(z^{-1}), B(z^{-1})$ jsou polynomy přenosu systému, $C(z^{-1})$ je polynom poruchy, e_s(k) je bílý šum a $\Delta =1-z^{-1}$ . Obecný systém druhého řádu je ve tvaru

$G(z^{-1}) = \frac{Y(z^{-1})}{U(z^{-1})} = \frac{b_1 z^{-1} + b_2 z^{-2}}{1+a_1 z^{-1} + a_2 z^{-2}} = \frac{B(z^{-1})}{A(z^{-1})}$

(18)

Po vynásobení rovnice (17) parametrem $\Delta$ , dosazení polynomu $C(z^{-1})=1$ a e_s(k)=0 byla získána rovnice ve tvaru

$\Delta A(z^{-1}) y(k) = B(z^{-1}) \Delta u(k)$

(19)

Do rovnice (19) byly dosazeny jednotlivé polynomy z rovnice (18)

$(1-z^{-1}) (1+a_1 z^{-1} + a_2 z^{-2}) y(k) = (b_1 z^{-1} + b_2 z^{-2}) \Delta u(k)$

(20)

roznásobeny a vyjádřeno y(k)

$y(k) = (1-a_1)y(k-1) + (a_2 - a_1) y(k-2) +$

$+ a_2 y(k-3) + b_1 \Delta u(k-1) + b_2 \Delta u(k-2)$

(21)

Rovnice (21) se nazývá rovnice výstupu. Pro přehlednost byly nahrazeny koeficienty jednotlivých parametrů rovnice (21)

$A=1-z^{-1}, \; B=a_2-a_1, \; C=a_2, \; D=b_1, \; E=b_2$

(22)

Po dosazení do rovnice (21) vznikla nová rovnice ve tvaru

$y(k) = A y(k-1) + B y(k-2) + C y(k-3) +$

$+ D \Delta u(k-1) + E \Delta u(k-2)$

(23)

V dalším kroku byly zvoleny jednotlivé horizonty prediktivního řízení

$N_1=1, \; N_2=4, \; N_u=4$

(22)

Pro odvození řídicího zákona bylo nutné odvodit čtyři prediktory výstupu a to postupným posunováním výstupní rovnice do budoucnosti $\tilde{y}(k+i)$ pro i=1,..,4. První rovnice prediktoru má tvar

$\tilde{y}(k+1) = A y(k) + B y(k-1) + C y(k-2) +$

$+ D \Delta u(k) + E \Delta u(k-1)$

(25)

Druhá rovnice prediktoru má tvar

$\tilde{y}(k+2) = A \tilde{y}(k+1) + B y(k) + C y(k-1) + D \Delta u(k+1) +$

$+ E \Delta u(k) = (AA+B) y(k) + (AB+C) y(k-1) + AC y(k-2) +$

$+ (AD+E) \Delta u(k) + AE \Delta u(k-1) + D \Delta u(k+1)$

(26)

Třetí rovnice prediktoru má tvar

$\tilde{y}(k+3) = (AA+B) \tilde{y}(k+1) + (AB+C) y(k) + AC y(k-1) +$

$+(AD+E) \Delta u(k+1) + AE \Delta u(k) + D \Delta u(k+2) =$

$= [A(AA+B)+(AB+C)] y(k) + [B(AA+B) +AC] y(k-1) +$

$+C(AA+B) y(k-2) + [D(AA+B)+AE]\Delta u +$

$+ E(AA+B)\Delta u(k-1) + (AD+E) \Delta u(k+1) + D \Delta u(k+2)$

(27)

Poslední rovnice prediktoru má tvar

$\tilde{y}(k+4) = [A(AA+B)+(AB+C)] \tilde{y}(k+1) +$

$+ [B(AA+B) +AC] y(k) ++ C(AA+B) y(k-1) +$

$[D(AA+B)+AE]\Delta u(k+1) + E(AA+B)\Delta u(k) +$

$+ (AD+E) \Delta u(k+2) + D \Delta u(k+3) =$

$= \{ A[A(AA+B)+(AB+C)] + [B(AA+B) +AC] \} y(k)$

$+ \{ B[A(AA+B)+(AB+C)] + C(AA+B) \} y(k-1)$

$+ \{ C[A(AA+B)+(AB+C)] \} y(k-2)$

$+ \{ D[A(AA+B)+(AB+C)] + E(AA+B) \} \Delta u(k)$

$+ \{ E[A(AA+B)+(AB+C)] \} \Delta u(k-1)$

$+ \{ [D(AA+B)+AE \} \Delta u(k+1) +$

$+ (AD+E) \Delta u(k+2) + D \Delta u(k+3)$

(28)

Rovnice (25), (26), (27) a (28) byly přepsány do maticového tvaru (9). Tímto zápisem je možné odvodit jednotlivé matice G a matice y₀. Matice G se nazývá Jacobián modelu. Jedná se o trojúhelníkovou matici, která obsahuje koeficienty, $\Delta u, .. , \Delta u(k+N_u-1)$ jednotlivých prediktorů, odezev modelu na jednotkový skok. Rozměr matice G je <N₂-N₁+1,N_u>.

$G = \left( \begin{array}{ccc} g_1 & 0 & 0 \\ g_2 & g_1 & 0 \\ g_3 & g_2 & g_1 \\ g_4 & g_3 & g_2 \end{array} \right)$

(30)

Pro výpočet matice G stačí vypočítat jen první sloupec matice.

$G_1 = \left( \begin{array}{c} D \\ AD+E \\ D(AA+B)+AE \\ D[A(AA+B)+(AB+C)] + E(AA+B) \end{array} \right)$

(31)

Zbylé členy y(k), y(k-1), y(k-2) a $\Delta u(k-1)$ jsou obsaženy v matici y₀, která se nazývá matice volné odezvy systému.

$y_0 = \left( \begin{array}{cccc} y_{0_{y(k)}} & y_{0_{y(k-1)}} & y_{0_{y(k-2)}} & y_{0_{y(k-3)}} \end{array} \right)$

(32)

Jednotlivé vektory matice y₀ mají tvar

$y_{0_{y(k)}} = \left( \begin{array}{c} A \\ AA+b \\ A(AA+B)+(AB+C) \\ A[A(AA+B)+(AB+C)] + [B(AA+B) + AC] \end{array} \right)$

(33)

$y_{0_{y(k-1)}} = \left( \begin{array}{c} B \\ AB+C \\ B(AA+B)+AC \\ B[A(AA+B)+(AB+C)] + C(AA+B) \end{array} \right)$

(34)

$y_{0_{y(k-2)}} = \left( \begin{array}{c} C \\ AC \\ C(AA+B) \\ C[A(AA+B)+(AB+C)] \end{array} \right)$

(35)

$y_{0_{y(k-3)}} = \left( \begin{array}{c} E \\ AE \\ E(AA+B) \\ E[A(AA+B)+(AB+C)] \end{array} \right)$

(36)

Z jednotlivých vektorů (31), (33), (34), (35) a (36) je zřejmé, že k určení dalších prvků jednotlivých vektorů stačí znát pouze první tři prvky vektoru každého parametru. Další prvky lze vypočítat pomocí třech posledních prvků vektoru, které se postupně vynásobí koeficienty A, B, C.

$v = \left( \begin{array}{c} v_1 \\ v_2 \\ v_3 \\ v_4 = Av_3+Bv_2+Cv_1 \end{array} \right)$

(37)

Tímto způsobem je možné vypočítat jednotlivé matice pro různé horizonty prediktivního řízení. Pokud jsou matice G a y₀ známé, mohou být dosazeny do rovnice

$\Delta u = K(w-y_0)$

(38)

kde K je první řádek matice Q

$Q=(G^T G+ \lambda I)^{-1}G^T$

(39)

kde I je jednotková matice, $\lambda$ je penalizační konstanta. Výsledný řídící zákon je ve tvaru

$\Delta u = k_1 w(k+1) + k_2 w(k+2) + k_3 w(k+3) + k_4 w(k+4)$

$+ r_1 y(k) + r_2 y(k-1) + r_3 y(k-2) + r_4 \Delta u(k-1)$

(40)

kde koeficienty k_j pro j=1,…,N₂ jsou prvky vektoru K, r_i pro i=1,…,2n (n – řád systému) jsou prvky prvního řádku matice R

$R=-K y_0$

(41)

Stejný postup odvození lze aplikovat také na systémy prvního nebo třetího řádu ať už s dopravním zpožděním nebo bez něj. Pokud jsou zanedbány omezující podmínky, úloha vede na jednoduché řešení řídicího zákona. V opačném případě je nutné do řešení zapojit také optimalizační metody.

Příklad

Byl zadán přenos spojitého systému druhého řádu

$G(s)=\frac{Y(s)}{U(s)} = \frac{3}{s^2+2s+1}$

(42)

který byl diskrétizován s periodou vzorkování T₀=0.5s

$G(z^{-1})=\frac{Y(z^{-1})}{U(z^{-1})} = \frac{0.2706 z^{-1} + 0.1937 z^{-2}}{1-1.213 z^{-1} + 0.3679 z^{-2}}=\frac{B(z^{-1})}{A(z^{-1})}$

(43)

Obr. 3: Přechodová charakteristika systému

Vzhledem k tomu, že se jedná o systém bez dopravního zpoždění, byl zvolen minimální horizont N₁=1. Z průběhu přechodové charakteristiky na Obr. 3 byl zvolen maximální horizont N₂=8 . Řídící horizont N_u=4 a penalizační konstanta $\lambda = 40$ byly zvoleny experimentálně. Jednotlivé prvky polynomů přenosu byly dosazeny do rovnic (22)

$A=2.213, \; B=-1.5809, \; C=0.3679, \; D=0.2706, \; E=0.1938$

(44)

Ze zvoleného maximálního horizontu N₂ je patrné, že pro sestavení matice G a y₀ bude nutné odvodit 8 prediktorů výstupu. Při aplikování pravidla (37) stačí odvodit pouze první tři prediktory výstupu. Výsledná matice má G a y₀ tvar

$G = \left( \begin{array}{cccc} 0.2706 & 0 & 0 & 0 \\ 0.7926 & 0.2706 & 0 & 0 \\ 1.3263 & 0.7926 & 0.2706 & 0 \\ 1.7816 & 1.3263 & 0.7926 & 0.2706 \\ 2.1375 & 1.7816 & 1.3263 & 0.7926 \\ 2.4018 & 2.1375 & 1.7816 & 1.3263 \\ 2.5914 & 2.4018 & 2.1375 & 1.7816 \\ 2.7214 & 2.5914 & 2.4018 & 2.1375 \end{array} \right)$

(45)

$y_0 = \left( \begin{array}{cccc} 2.213 & -1.5809 & 0.3679 & 0.1938 \\ 3.3165 & -3.1306 & 0.8142 & 0.4289 \\ 4.2087 & -4.4288 & 1.2201 & 0.6427 \\ 4.885 & -5.4334 & 1.5484 & 0.8156 \\ 5.3772 & -6.1744 & 1.7972 & 0.9467 \\ 5.7253 & -6.7036 & 1.9783 & 1.0421 \\ 5.9665 & -7.0729 & 2.1063 & 1.1096 \\ 6.1311 & -7.3261 & 2.1951 & 1.1563 \end{array} \right)$

(46)

Tyto matice byly dále dosazeny do rovnice (39) a (41) a vypočítán řídící zákon podle (40)

$K = [0.0041 \; 0.0109 \; 0.0159 \; 0.0183 \; 0.0189 \; 0.0188 \; 0.0184 \; 0.0179]$

(47)

$R = \left[ \begin{array}{cccc} -0.63 & 0.7141 & -0.2072 & -0.1092 \end{array} \right]$

(48)

$\Delta u = 0.0041 w(k+1) + 0.0109 w(k+2) + 0.0159 w(k+3) +$

$+ 0.0183 w(k+4) + 0.0189 w(k+5) + 0.0188 w(k+6) +$

$+ 0.0184 w(k+7) + 0.0179 w(k+8) -0.63y(k) +0.7141 y(k-1) -$

$-0.2072 y(k-2) + 0.1092 \Delta u(k-1)$

(49)

V programovém prostředí MATLAB byl vytvořen skript, pomocí kterého se vypočítaly jednotlivé matice G a y₀, následně provedla simulace a nakonec vykreslil průběh regulace Obr. 4.

Obr. 4: Průběh regulace

Závěr

Cílem tohoto článku bylo seznámení se základy prediktivního řízením a jeho pojmy, které je v této době čím dál více oblíbené. V první části byly popsány základní principy a pojmy prediktivního řízení. Druhá část byla zaměřena na obecný výpočet řídicího zákona prediktivního řízení pro systém druhého řádu bez omezení. V poslední části byl odvozený řídicí zákon simulačně ověřen na konkrétním systému.

Poděkování

Tato práce vznikla za podpory výzkumného záměru Ministerstva školství mládeže a tělovýchovy České Republiky MSM 7088352101 a grantu Univerzity Tomáše Bati ve Zlíně IGA/55/FAI/10/D.

Použitá literatura

MIKLEŠ, Ján; FIKAR, Miroslav. Process Modelling, Identification, and Control. Berlín : Springer Verlag, 2007. 480 s. ISBN 978-3-540-71969-4.
CLARKE, D. W.-MOHTADI, C.-TUFFS, P. S.: Generalized Predictive Control. Part I. The Basic Algorithm, Generalized Predictive Control. Part II. Extensions and Interpretations, Automatica 23 (1987), 137-160.
KANJILAL, P. P.: Adaptive Prediction and Predictive Control, Peter Peregrinus, U. K., 1995.
MACIEJOWSKI, J. M.: Predictive Control with Constraints, Prentice Hall, Harlow, 2002.
SUNAN, H.-T. K. KIONG, K.-HENG, L. T. Applied Predictive Control, Springer-Verlag, London, 2002.
ROSSITER, J. A.: Model Based Predictive Control: A Practical Approach, CRC Press, Boca Raton, Florida, 2003.
CAMACHO, E. F.-BORDONS, C.: Model Predictive Control, Springer-Verlag , London, 2004.
BOBÁL, Vladimír, et al. Self-tuning Predictive control of Nonlinear Servo-motor. Journal of Electrical Engineering. 2010, 6. ISSN 1335-3632.

O časopise

Meta

RSS

Výpočet obecného řídícího zákona prediktivního řízení pro systému druhého řádu bez omezení

Napísať príspevok

Rubriky

Burza práce

Štúdijné materiály

Archív