Časový útok využívajúci cache kolízie na posledné kolo šifry AES
27. Február, 2012, Autor článku: Loderer Marek, Informačné technológie, Študentské práce
Ročník 5, číslo 2  Pridať príspevok
Pridať príspevok
![]() Medzi najúčinnejšie spôsoby, ktorými je možné kompromitovať šifry patria útoky na implementáciu šifier ako napríklad analýza postranných kanálov. Príspevok sa venuje neinvazívnemu pasívnemu útoku – analýze doby výpočtu šifry AES, softvérovo implementovanej v knižnici OpenSSL vo verziách 0.9.8a, 0.9.8b a 0.9.8k. Tieto verzie sa od seba líšia rôznym implementovaním posledného kola šifry AES, čo mení správanie sa cache pamäte, ktorá má značný vplyv na dobu výpočtu stavu šifry AES.
Medzi najúčinnejšie spôsoby, ktorými je možné kompromitovať šifry patria útoky na implementáciu šifier ako napríklad analýza postranných kanálov. Príspevok sa venuje neinvazívnemu pasívnemu útoku – analýze doby výpočtu šifry AES, softvérovo implementovanej v knižnici OpenSSL vo verziách 0.9.8a, 0.9.8b a 0.9.8k. Tieto verzie sa od seba líšia rôznym implementovaním posledného kola šifry AES, čo mení správanie sa cache pamäte, ktorá má značný vplyv na dobu výpočtu stavu šifry AES.
Využitím útokov publikovaných Josephom Bonneauom , v 2006, [1, 5], sa ukazuje, že útok má pre OpenSSL verzie 0.9.8c a novšie, vyššiu zložitosť, ktorá však stále nie je dostatočná. Preto, na potreby zabezpečenia odporúčame použiť protiopatrenia akými sú napríklad tzv. skrývanie a maskovanie. Pri útokoch využívajú slabinu pamäte cache. Dôležité sú znalosti o architektúre procesora použitého počítača, možnosť veľmi presne merať počet cyklov procesora pomocou inštrukcie RDTSC a možnosť poznať lokalizáciu T-boxov AES-u v pamäti.
1. Úvod
Útoky postrannými kanálmi boli experimentálne demonštrované proti viacerým kryptosystémom. Je to preto, že šifra nie je v skutočnosti len matematickou funkciou (1) – ideálny prípad, ale funkciou (2), kde t je pridaná informácia produkovaná fyzickou implementáciou. [1, str. 1]
| (1) |
| (2) |
Útok, ktorý bude popísaný využíva časový efekt cache kolízií, ktoré umožňujú zistiť vzťahy medzi bajtmi tajného kľúča. V rámci finálneho vyhodnotenia šifry Rijndael, sa NIST vyjadril, že operácie vo vyhľadávacích tabuľkách „nie sú zraniteľné, citlivé, pri časových útokoch“ a považoval Rijndael za najjednoduchší spomedzi finalistov schopný ubrániť sa útokom postrannými kanálmi. [1, str. 1, 2]
V porovnaní s predpoveďami NIST-u, sú z preštudovanej literatúry (Tab. 1) uvedené rôzne už uskutočnené útoky na šifru AES spolu s ich náročnosťou na počet vzoriek.
Tab. 1. Prehľad časových útokov [1, str. 2; 3, str. 5]
| Autor útoku | Útok na kolo resp. kolá | Počet vzoriek | Výsledok |
|---|---|---|---|
| Bernstein | Prvé | 227,5 | Celý kľúč |
| Tsunoo et al. | - | 226 | Celý kľúč |
| Aciicmez | Dve | 222,63 | Celý kľúč |
| Osvik et al. | Dve | 218,93 | Celý kľúč |
| Bonneau et al. | Posledné | 215 | Celý kľúč |
| Bonneau et al. | Prvé | 214,58 | 60 bitov |
| Bonneau et al. | Posledné (vylepšený) | 213 | Celý kľúč |
| Zhao et al. | Prvé | 28,45 | Celý kľúč |
| Osvik et al. | Dve | 28,22 | Celý kľúč |
| Neve | Posledné (neeliminačná metóda) | 27,64 | Celý kľúč |
| Zhao et al. | Dve | 26,32 | Celý kľúč |
| Neve | Posledné (eliminačná metóda) | 24,32 | Celý kľúč |
2. Cache jej činnosť a štruktúra
Jadrom moderných počítačov a mobilných zariadení je procesor alebo mikroprocesor. Ten vykonáva inštrukcie a spracováva dáta programov a operačného systému. Dáta sú prenášané z pevného disku do operačnej pamäte. Problém je v tom, že hlavná pamäť nie je tak rýchla ako procesor (CPU). Ako prevencia proti neželanej čakacej dobe, existuje malá, zato rýchla pamäť pridaná k procesoru, nazývaná cache. Jej kapacita je malá v porovnaní s operačnou pamäťou. Výkon cache je dosiahnutý odlišným návrhom v porovnaní s operačnou pamäťou.
Cache je statická pamäť „Static Random Access Memory“ (SRAM). Pri tomto type je jeden bit a jeho inverzia uchovávaná dvomi krížovo – spojenými (cross-coupled) invertormi. Uložené údaje sa neobnovujú, indikuje to slovo static. Operačná pamäť je dynamická „Dynamic Random Access Memory“ (DRAM), kde je jeden bit uchovaný v kondenzátore. Údaje sa musia periodicky obnovovať, pretože informácia uložená v kondenzátore sa postupne stráca.
Kompromisom je malá cache pridaná k CPU. Tá zmierňuje časový odstup medzi operačnou pamäťou a CPU ukladaním dát, ktoré budú pravdepodobne čoskoro spracovávané. [2, str. 8] Cache je usporiadaná do 2L cache lines (riadkov). Každý riadok uchováva 2B bajtov. Teda veľkosť cache je 2L+B bajtov. Asociatívna cache je rozdelená do S cache sets (setov). Každý set obsahuje W cache riadkov. Každý riadok má B bajtov. Teda veľkosť cache je S.W.B. Tieto hodnoty sa v Linuxe nachádzajú v nasledujúcich súboroch (príklad pre L1 cache):
/sys/devices/system/cpu/cpu0/cache/index0/.
./coherency_line_size B
./number_of_sets S
./ways_of_associativity W
./size S.W.B
Ak CPU potrebuje nejaké dáta, najskôr skontroluje, či sú už v cache. Pre túto operáciu sa časť adresy, ktorá reprezentuje cache riadok, tzv. „tag“, porovnáva s hodnotami v tag-RAM. Ak je porovnávanie úspešné, dáta sú v cache. Toto je cache hit a dáta sú spracované bez prístupu do operačnej pamäti. V prípade, že nastal cache miss, sú dáta prenesené z operačnej pamäti a uložené do cache. Vždy je prenesený celý cache riadok. Trvá to viac hodinových cyklov, kým CPU môže spracovať dáta v porovnaní s prípadom cache hit.
Existujú techniky ako zlepšiť základný operačný mód a zlepšiť tak pomer cache hits a misses. Jednou metódou je „direct-mapped“ cache, ktorá je jednoduchá, rýchla, ale má veľký pomer cache misses. „Fully associative“ cache, ktorá však dlhšie porovnáva, ale má nízky počet cache misses. Kombináciou výhod predchádzajúcich metód je „n-way set associative“ cache. Má dobrý pomer cache hit a miss. Príklad takéhoto modelu je na obrázku (Obr. 1). [2, str. 8-9]
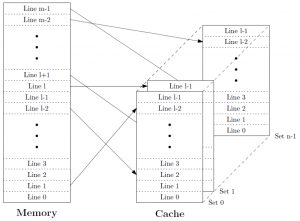
Obr. 1. Model „n-way set associative“ cache [2, str. 10]
Teda je zrejmé, že cache hit alebo miss môže vplývať na počet hodinových cyklov CPU alebo spotrebu energie. Pre bežné procesory cache hit trvá približne 3 cykly, kým cache miss 12 – 100 cyklov. Keď dva rôzne procesy pristúpia k dátam, ktoré sú mapované do rovnakého cache setu (resp. cache riadku) možno detegovať nižší počet cyklov. [3, str. 2]
3. Cache kolízie
Veľkosť cache riadku sa pohybuje v rozmedzí 32B pre Pentium III a 64B, 128B alebo viac pre Pentium IV a AMD procesory. Veľkosť jedného prvku AES T-boxu sú 4 bajty. To znamená, že pre Pentium IV a Core 2 Duo sa podľa (3) δ = 16. Teda 16 prvkov AES T-boxu zdieľa jeden cache riadok.
| (3) |
Preto pre bajty lu a lw , možno ignorovať posledných, najnižších, log2δ bitov. V tomto prípade sú to 4 bity. Nech <lu>4 = <lw>4 znamená, že lu a lw sa zhodujú v 4 najvýznamnejších bitoch (vo zvyšných 4 bitoch sa môžu líšiť). V tomto prípade vyhľadanie adresy lu adresou lw spôsobí cache hit. Ak <lu> ≠ <lw>, potom lw spôsobí cache miss. [1, str. 6]
V prípade, že indexy lu = lw, hovoríme o tzv. priamom cache hit. V prípade, že platí <lu>4 = <lw>4, hovoríme o tzv. riadkovom cache hit. Na obrázku (Obr. 2) je znázornený vplyv počtu kolízií na počet cyklov. Ako môžeme vidieť pri počte kolízií menej ako 11 je jasná korelácia, kedy sa počet cyklov neznižuje na rozdiel od predchádzajúcich úvah. [1, str. 6]

Obr. 2. Vplyv počtu kolízií v poslednom kole na počet cyklov, Pentium III. [1, str. 7]
4. Generovanie kľúča
Algoritmus generovania podkľúčov (AGP) expanduje kľúč a tým generuje kľúče pre jednotlivé kolá. Pre AES-128b sa používa 11 kľúčov. Každý z týchto kľúčov je tvorený štyrmi štvorbajtovými slovami. Tajný kľúč sa použije na inicializáciu. Činnosť algoritmu znázorňuje obrázok (Obr. 3). [2, str. 21]
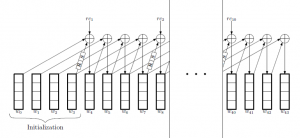
Obr. 3. Grafické znázornenie procesu generovania podkľúčov. [2, str. 22]
Pri generovaní podkľúčov sa používa S-box, cyklická rotácia bajtov o jeden bajt a rci, čo je kolová konštanta, resp. prvok z poľa GF(28). Rovnice akým spôsobom sa generujú podkľúče sa nachádzajú v [2, str. 22].
5. Útok na posledné kolo
AES je bloková šifra typu SPN (substitučno-permutačná sieť). Využíva operácie AddRoundKey (operácia XOR), SubBytes (aplikácia S-boxu), ShiftRows (permutácia, posun riadkov) a MixColumns (prenásobenie maticou, lineárna operácia). Pri softvérovej implementácii sú operácie SubBytes, ShiftRows a MixColumns nahradené predpočítanými tabuľkami. Šifra v poslednom kole nepoužíva operáciu MixColumns.
Softvérová implementácia používa tabuľku T4, ktorú tvorí S-box. V poslednom desiatom kole (pri AES-128b) sa používa 11. 16 bajtový blok kľúča. Princíp ako sa tvorí 176 bajtov kľúča bol uvedený v bode 4. Pretože AGP AES-u je konečný automat a ak poznáme celý stav kľúča môžeme sa pohybovať smerom dopredu aj dozadu. Táto vlastnosť AGP bola súčasťou originálneho návrhu šifry Rijndael. [1, str. 3]
Ak útočník dokáže obnoviť 16 bajtov kľúča z posledného kola, dokáže obnoviť originálny kľúč. Tento útok sa snaží využiť priame kolízie v poslednom kole. Posledné kolo sa realizuje podľa (4). [1, str. 8]
| (4) |
Kde C je výstupný zašifrovaný text, X je vstup pre dané kolo rozdelený na xi10 a K je expandovaný tajný kľúč pre posledné kolo rozdelený na ki10. Dôležitým faktom je, že S-box je nelineárna permutácia všetkých 256 možností pre hodnotu jedného bajtu. Predpokladajme, že platí (5). Potom pri šifrovaní podľa (6) nastane cache hit.
| (5) |
| (6) |
V tomto prípade sa to odrazí na kratšom čase šifrovania. Na tomto základe možno určiť vzťah medzi bajtmi kľúča podľa (7) a po úprave (8).
| (7) |
| (8) |
Existuje ešte prípad (9). Úspech útoku aj v tomto prípade, je zaručený samotnými vlastnosťami S-boxu. Spôsobuje to nelinearita S-boxu.
| (9) |
V tomto prípade už (6) nenastane a zmení sa na (10). Preto už v danej podobe neplatí (7), a ani (8).
| (10) |
Teraz už platí (11).
| (11) |
Pretože α, β sú výsledkami S-boxu je hodnota γ rôzna od nuly. Indexy, ktoré budú vyhľadané v S-boxe produkujú α, β v podstate náhodne vzhľadom na kvalitu nelinearity S-boxu. Teda v prípade, že platí (5) nastane priamy cache hit, inak nastane vyhľadanie na dvoch v podstate náhodných pozíciách v T4. [1, str. 8]
6. Zámer útoku
Zámerom útoku je uložiť zašifrované texty C s príslušným časom t do poľa s použitým tajným kľúčom K. Cieľom je zo známych hodnôt ci nájsť podľa (8) také hodnoty Δi,j* pre každé i, j, kde i ≠ j tak, aby čas šifrovania bol menší ako je priemer pre všetky zašifrované texty. Potom také Δi,j* vedú ku odhadom pre jednotlivé bajty tajného kľúča. S touto znalosťou môže útočník vytvoriť tzv. reťaz vzťahov. Ide v podstate o sústavu lineárnych rovníc kde sa modifikáciou jedného bajtu menia všetky bajty v danej reťazi. [1, str. 8]
Napríklad ak poznáme tri delty pre päť bajtov Δ0,3=0x10, Δ3,4=0xF0, Δ1,2=0xAF útočník nemusí prehľadávať všetkých 2565 = 240 možností, ale stačí prejsť len 2562 = 216 možností.
Útok je implementovaný v podobe konzolového programu aes_attack napísaný v jazyku C. Zdrojové súbory útoku pochádzajú zo zdroja [5]. Algoritmus najprv zašifruje 220 otvorených textov. Pred každým šifrovaním sa vyčistí buď L1 alebo L2 cache. Na záver sa inkrementálnym spôsobom tieto dáta spracúvajú, pokiaľ sa nepodarí obnoviť správny tajný kľúč. [1, str. 16]
6.1. Algoritmy na odhadovanie kľúča
Útok využíva dva algoritmy pri odhadovaní kľúča. Prvým je „Random Walk“, ktorý je variantom lokálne optimalizovaného prehľadávania. Druhým je „Belief Propagation“, ktorý sa na základe pravdepodobnostnej aproximácie snaží dáta mapovať na normálne rozdelenie, kde sú stredné hodnota a štandardná odchýlka známe. Podrobnejšie informácie o činnosti týchto algoritmov sa nachádzajú v [1, str. 18].
7. Protiopatrenia
Cieľom je kompromis medzi bezpečnosťou a výkonom. Možnosťami sú napríklad konštantný čas, zahrievanie cache, bucketing alebo softvérové riešenia. Podrobnejšie informácie o týchto metódach sú uvedené v [2, str. 12-13]. Brickell et al. popísal niekoľko iných možností ako napríklad predčítanie tabuliek, použitie menších tabuliek a náhodnú permutáciu tabuliek pri každom šifrovaní. [1, str. 12]
7.1. Softvérové riešenia
Spôsobom ako sa brániť proti útokom postrannými kanálmi je modifikácia samotného hardvéru. Ďalším riešením je zamerať sa na samotnú softvérovú implementáciu. Výpočet v poslednom kole, ktorý produkuje štyri bajty výstupného stavu vyzerá nasledovne (12). [1, str. 12]
| (12) |
Zraniteľnosť posledného kola resp. T4 možno znížiť opätovným použitím predchádzajúcich tabuliek T0,…,T3 podľa (13). [1, str. 12]
| (13) |
Ďalším riešením je použitie tabuľky T4, ktorej prvky majú veľkosť len jeden bajt. Tu autor J. Bonneau podotýka, že: „Nie je žiadny zjavný dôvod prečo originálna implementácia používa tabuľku T4 s prvkami veľkosti 4 bajty. Snáď len preto, aby bol kód zhodný s kódom predchádzajúcich kôl.“ [1, str. 13]. V tomto prípade sú operácie & nahradené posunmi nasledovne (14). [1, str. 13]
| (14) |
Implementácia (14) zvyšuje hodnotu δ podľa (3). Teraz sa už δ = 64, čo znižuje pravdepodobnosť cache kolízií. Pre δ = 16 je pravdepodobnosť cache miss 40,51%, zatiaľ čo pre δ = 64 je to len 1,78%. [1, str. 13]
Počas sledovania vývoja implementácie AES v OpenSSL tvorcovia naozaj využili niektoré z navrhovaných možností. Preto už OpenSSL verzia 0.9.8.c pri šifrovaní vôbec nevyužíva tabuľka T4. Tá je nahradená využitím predchádzajúcich tabuliek T0,…,T3. Pri dešifrovaní je tabuľka T4 s prvkami veľkosti 4 bajty nahradená T4 s prvkami veľkosti 1 bajt. [4]
8. Výsledky meraní
Merania boli uskutočnené na dvoch rôznych platformách s hardvérovou konfiguráciou podľa (Tab. 2). Program bol spustený s použitím náhodne vygenerovaných tajných kľúčov, postupne používal 215 vzoriek a každé meranie bolo zopakované 30 krát.
Tab. 2. Hardvérová konfigurácia
Prvý útok bol uskutočnený na OpenSSL v.0.9.8a. Dosiahnuté výsledky sú uvedené v tabuľke (Tab. 3).
Tab. 3. Výsledky útoku na verziu 0.9.8a
| Počet vzoriek | Čistenie L1 cache | Čistenie L2 cache | ||
|---|---|---|---|---|
| PC1 | PC2 | PC1 | PC2 | |
| Min | 217,59 | 218,17 | 217,81 | 218,00 |
| Max | 218,70 | 219,86 | 218,91 | 219,32 |
| Medián | 218,00 | 219,17 | 218,32 | 218,64 |
| Priemer | 218,14 | 219,14 | 218,33 | 218,65 |
Druhý útok bol uskutočnený na OpenSSL v.0.9.8b. Táto a aj predchádzajúca verzia využívajú v poslednom kole vyhľadávaciu tabuľku T4, kde sa výstupný stav počíta podľa (12). Dosiahnuté výsledky sú uvedené v tabuľke (Tab. 4).
Tab. 4. Výsledky útoku na verziu 0.9.8b
| Počet vzoriek | Čistenie L1 cache | Čistenie L2 cache |
|---|---|---|
| PC1 | PC2 | |
| Min | 217,32 | 218,00 |
| Max | 218,81 | 218,91 |
| Medián | 218,17 | 218,32 |
| Priemer | 218,01 | 218,35 |
Posledný útok bol realizovaný na OpenSSL v.0.9.8k, ktorá používa T4 s prvkami veľkosti jeden bajt. Tu s výstup počíta podľa (14). Použitý bol ten istý algoritmus výpočtu ako pri predošlých útokoch.
Tab. 5. Výsledky útoku na verziu 0.9.8k
| Počet vzoriek | Čistenie L2 cache |
|---|---|
| PC1 | |
| Min | 223,59 |
| Max | 224,59 |
| Medián | 224,00 |
| Priemer | 224,46 |
V grafe (Graf 1.) sú porovnané náročnosti na počet vzoriek pre útoky na jednotlivé verzie OpenSSL.
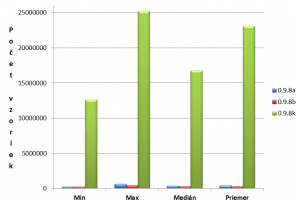
Graf 1. Porovnaní náročnosti na počet vzoriek
9. Zhrnutie
V porovnaní s údajom v (Tab. 1) sa počet vzoriek 215 len málo odlišuje od tých, ktoré boli dosiahnuté na použitých počítačoch 218,32 a 218,64. Útok má podobnú náročnosť na počet vzoriek pre verziu 0.9.8a a 0.9.8b, pretože sa softvérové implementácie od seba výrazne nelíšia.
Pri útoku na verziu 0.9.8k, kde sa už nachádza iný AES T-box sa počet vzoriek zväčšil 40-50 násobne. Tento nárast je spôsobený znížením počtu cache misses v poslednom kole (v bode 7.1). Teda navrhované softvérové riešenia sú naozaj účinné a ako už bolo spomenuté v bode 7.1 autori OpenSSL ich skutočne aj využili.
Útoky vyžadujú znalosti o architektúre procesora použitého počítača, možnosť veľmi presne merať počet cyklov procesora pomocou inštrukcie RDTSC a možnosť poznať lokalizáciu T-boxov AES-u v pamäti. Námetom na ďalšiu prácu by mohlo byť podrobnejšie preštudovanie činnosti cache a CPU súčasných počítačov, použitie vylepšeného útoku na posledné kolo (Expanded Final Round Attack), ktorý tiež implementoval Joseph Bonneau v [1, 5].
10. Odkazy na literatúru
- Bonneau, J., et. al., Cache-Collision Timing Attacks Against AES, [online], [citované 3.4.2011], Dostupné z
http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.165.7844&rep=rep1&type=pdf - Wienecke, M., Cache based Timing Attacks Embedded Systems, [online], [citované 3.4.2011], Dostupné z
www.crypto.rub.de/imperia/md/content/texte/theses/ms wienecke.pdf - Zhao, X., et. al., Robust first two rounds access driven cache timing attack on AES, [online], [citované
3.4.2011], Dostupné z
www.informatics.org.cn/doc/ucit200906/ucit20090605.pdf - OpenSSL, OpenSSL: Source, [online], [citované 23.4.2011], Dostupné z
http://www.openssl.org/source/ - Joseph Bonneau, Joseph Bonneeau – Research Projects, [online], [citované 3.4.2011], Dostupné z
http://www.jbonneau.com/research.html
Spoluautorom článku je Ing. Marek Repka, Katedra aplikovanej informatiky a výpočtovej techniky, Fakulta elektrotechniky a informatiky, Slovenská technická univerzita, 812 19 Bratislava, Slovenská republika
Práca bola prezentovaná na Študentskej vedeckej a odbornej činnosti (ŠVOČ 2011) v sekcii Aplikovaná informatika, ISBN 978-80-227-3508-7

