First part is a look at the history of an algorithm. Then follows its definition and next part is focused on the main properties of algorithms. That should give reader better insight into the topic. This part is followed by different types of algorithms; there will be told a little bit about their strengths and weaknesses. Last part is about presentation and writing of algorithms.

1. History and Origin of an Algorithm

The word „algorithm“ is derived from a name of a major Persian mathematician Abd Allāh Muhammad ibn Mūsā al-Khwārizmī, who lived in the first half of 9th century. This mathematician practically created the system of Arabic numerals and basic algebra (specifically, methods for solving linear and quadratic equations). His name was transferred into Latin as „algorismus“, over time as „algorithm“, what originally meant „the implementation of arithmetic using Arabic numerals“.

2. Definition of an Algorithm

An algorithm is often defined as precise instructions or steps which are used to solve a given type of task. This definition seems to be true; however, by further research could find out that it is not very accurate. The accurate definition of an algorithm is – an algorithm is a procedure which can be done by Turing machine. Turing machine is a theoretical computer model described by the mathematician Alan Turing.

It consists of a processor unit formed by a finite automaton and a program in the shape of the transition rules function and a potentially infinite tape for writing intermediate results and data inputs. An algorithm is a schematic procedure for solving a certain kind of problem, which is implemented using a finite number of well-defined steps. Although, this term is now used mainly in a computer science and natural sciences in general, so its scope is much broader (kitchen recipes, instructions, …).

Figure 1. An algorithm

3. Properties of Algorithms

In practice, an algorithm is denoted by prescription, which has the following properties:

• It is clever, that makes work easier.
• This applies to repetitive activities.

Creating an algorithm is certainly very hard mental work. There is no point wasting it on things unique to one person, that will not be repeated and that nobody needs. An algorithm usually works with some inputs, variables and activities. Inputs have a defined set of values which may be acquired. An algorithm has at least one output, which is required in relation to specific inputs and thus form the answer to a problem that the algorithm is supposed to solve. Algorithms have to be finite, definite, effective and general.

Finiteness

Each algorithm must terminate after a finite number of steps. This number can be arbitrarily large (depending on the extent and values of the input data) but for every input it must be finite. Procedures that do not meet this condition could be called computing methods. The special example of an infinite computing method is a reactive process which continuously interacts with the environment.

Definiteness

Each step of an algorithm must be clearly and precisely defined, in each situation must be quite clear what and how to do – no step can be interpreted in multiple ways. Because a plain language generally does not provide absolute accuracy and clarity of expression, the programming language was designed. In this language, each command has a clearly defined meaning. Expression of computational methods in a programming language is called program.

Effectiveness

Generally, we require that an algorithm to be effective in a sense that every procedure should be simple enough to be realizable. This means that instructions can be at least in principle performed in finite amount of time using only pencil and paper.

Generality

An algorithm does not solve one specific problem (for example how to calculate 8 + 9) but the general class of similar problems (for example how to calculate the sum of two integers).

4. Partitioning of Algorithms

Recursive and iterative algorithms

An iterative algorithm is one that lies in the repetition of certain of its parts (block). A recursive algorithm repeats the code through a call to itself (usually on smaller sub-problems). Every recursive algorithm can be converted into an iterative form. The advantage of recursive algorithms is their easily readable and compact notation. The disadvantage is a consumption of additional system resources to maintain each recursive call.

Deterministic and nondeterministic algorithms

A deterministic algorithm is one that allows in every step just one way to proceed. A nondeterministic algorithm allows more ways. An example could be deterministic and nondeterministic automata.

Serial, parallel and distributed algorithms

A serial algorithm performs all steps in series (one after the other). A parallel algorithm performs the following steps simultaneously (multi-train) and a distributed algorithm is designed to run simultaneously on multiple machines.

Asymptotic complexity of an algorithm

Asymptotic complexity of an algorithm is characterized by the number of transactions, depending on data size. For example, if the algorithm walks through a field, then the complexity is linear (for each element is assigned a constant number of operations).

Class P – contains problems decidable in polynomial time. Class NP – it is possible to verify their solution in polynomial time.

5. Types of Algorithms

Recursive algorithms

This algorithm calls itself with smaller input values in each step. Base cases are solved directly and immediately and then the algorithm backtracks to find a simpler solution. Generally, recursive computer programs require more memory and calculations compared to other algorithms, but they are simpler and in many cases natural problem solvers.

Backtracking algorithms

Backtracking algorithms try to find the solution. If the solution is found, the algorithm stops. Otherwise, it continues to backtrack and test again until the solution is found.

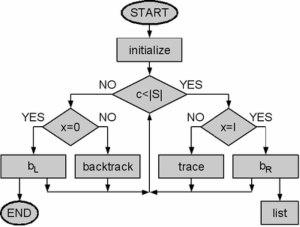
Figure 2. Example of a backtracking algorithm flow chart

Divide and conquer

This algorithm divides the problem into smaller sub-problems of a same type which are recursively applied (up to trivial sub-problems that can be solved directly). Then the partial solutions are appropriately combined. Traditionally, an algorithm is only called divide and conquer if it contains two or more recursive calls. This algorithm is used for example to solve Hanoi towers puzzle. In the case that more than one computer (or one processor core) is available, the task can be divided between them – this goal is dedicated to parallel algorithms.

Dynamic programming

This kind of algorithm remembers past results and uses them to find new results. Dynamic programming is usually used if there are multiple solutions and we need to find the best one. It works on a principle that the algorithm gradually solves the problems from simplest to more complex, by using the results of already solved simpler sub-problems. This algorithm is used for example to count Fibonacci number.

Greedy algorithms

Greedy algorithms work well for optimization problems. The term „optimization problem” means a problem when finding solution is not good enough and the best solution is needed. It works in phases. In every phase the best solution is taken which will further lead to the best overall solution. Once a choice is made, it is not possible to backtrack later.

Branch and bound algorithms

As an algorithm progress, a tree of sub-problems is formed to the root which is the original problem. It follows each branch until it is either solved or concentrated with another branch. It is used for example to solve problems when minimal total distance travelled between unspecified amounts of points is needed.

Brute force algorithms

It starts from a random point and uses every possibility until the solution is found. It is easier to implement but very slow and cannot be applied to a problem which have a big input size.

Probabilistic algorithms

This class contains any algorithm which made some decisions randomly or pseudo-randomly.

Genetic algorithms

Genetic algorithms work by mimicking biological evolutionary processes, the gradual growing the best solutions through mutation and crossbreeding. In genetic programming, this procedure is applied directly to algorithms that are interpreted as a possible solution.

Heuristic algorithms

The goal is not to find the exact solution, but a suitable approximation. This is used in situations where the available resources (e.g. time) are not sufficient to use exact algorithms (or if no suitable exact algorithm is known at all).

6. Presentation and Writing of Algorithms

There are few ways to present or write down an algorithm. Like a natural language in text, a pseudo-language, a flowchart, a structural diagram, a kopenogram, and finally a program. Of course, it can be described verbally by a natural language. A graphical representation by a flowchart using specific symbols and shortcuts is the most typical option.

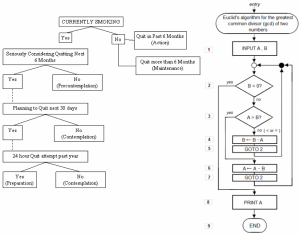
Figure 3. Two examples of flow charts

Acknowledgment

This paper was supported by the Internal Grant Agency of TBU in Zlín, project No. IGA/FAI/2012/015.

References

1. An algorithm [online]. 2011-11-29 [Cit. 2011-11-29]. Available from WWW:
   http://www.webopedia.com/FIG/ALGOR.gif
2. Algorithms [online]. [Cit. 2011-12-03]. Available from WWW:
   http://www.algoritmy.net/
3. Introduction to the theory of algorithms [online]. [Cit. 2011-12-04]. Available from WWW:
   http://www.islandsoft.cz/index.php?art=uvod-do-teorie-algoritmu-definice-casova-slozitost-stabilita
4. An algorithm [online]. [Cit. 2011-12-04]. Available from WWW:
   http://kisk.phil.muni.cz/wiki/Algoritmus
5. Algorithms: Introduction to the theory [online]. [Cit. 2011-12-02]. Available from WWW:
   http://www.manualy.net/article.php?articleID=12
6. Algorithms [online]. [Cit. 2011-12-04]. Available from WWW:
   http://objekty.vse.cz/Programovani/CoJeANeniAlgoritmus
7. Algorithmic solvability of problems [online]. [Cit. 2011-10-15]. Available from WWW:
   http://www.kiv.zcu.cz/~netrvalo/vyuka/ppa2-05/ekniha/online/HTML/51/default.htm
8. An algorithm [online]. [Cit. 2011-12-04]. Available from WWW:
   http://cs.wikipedia.org/wiki/Algoritmus
9. WRÓBLEWSKI, Piotr. Algorithms: Data Structures and Programming Techniques. Brno: Computer Press, 2004. ISBN 80-251-0343-9.