Článok poukazuje na veľké výhody použitia technológií Grid a GPGPU pri výpočtoch desiatok až stovák 2D rezov hraničnej plochy. Tie tvoria základ pre jej rekonštrukciu v sekvenčných a chaos generujúcich obvodoch v 3D stavovom priestore. Navyše, v porovnaní s niekoľkými osobnými počítačmi, sa technológia GPGPU ukázala 15 až 100 násobne rýchlejšia, čo poukazuje na jej dobré využitie v budúcnosti. Spolu s uvedením do prevádzky Slovenskej infraštruktúry pre vysokovýkonné počítanie, sa ponúkajú veľké možnosti pre výpočtovo náročné úlohy podobné tým, ktoré sú predstavené v tomto príspevku.

Úvod

Práca [1] poukázala na možnosti výpočtu rezov hraničnej plochy (HP) použitím osobných počítačov (PC) a na jej význam v sekvenčných a chaos generujúcich obvodoch. Použitie PC na uvedené výpočty je vpodstate prirodzenou samozrejmosťou. Po vytvorení programu (napr. v jazyku C), ktorý rieši metódou Runge – Kutta systém troch diferenciálnych rovníc prvého rádu a jeho odladení, nasleduje spustenie programu. Keďže takto vytvorené programy nepracujú s maticami, nemajú veľké nároky na operačnú pamäť a na časté či objemné zápisy výsledkov na harddisk, tak v závislosti od výkonnosti procesora (CPU) počítača, je možné s väčším či menším odstupom času získať výsledky – rezy HP.

V prípade jednoprocesorového PC však ide o možnosť spustenia jedného programu s možnosťou spustenia ďalšieho až po ukončení predchádzajúceho programu. Aj keď vďaka multitaskingu bola možnosť spustenia viacerých programov súčasne, bolo to neefektívne, pretože čas výpočtu sa neúmerne predlžoval prepínaním procesora medzi viacerými bežiacimi programami.

Pre potreby 3D vizualizácie HP je však potrebné vypočítať rádovo desiatky až stovky 2D rezov HP. Pri ich výpočte ide vlastne o výpočet množiny rovinných rezov. Jeden z nich ilustruje obr. 1 [2]. Ten je zložený z matice MxN bodov, pričom nasledujúci rez sa od predchádzajúceho líši iba v jedinom parametri, a to vo zväčšujúcej sa napäťovej resp. prúdovej úrovni. Takto z paralelných rezov v 3D priestore je možné vytvoriť trojrozmerný model HP [2], [3].

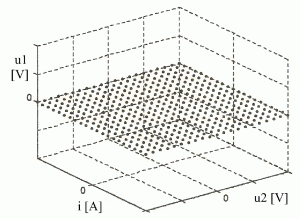
Obr. 1 Výpočet 2D rezu HP pri zvolenom počte bodov MxN.

Výpočet veľkej množiny HP bolo možné sparalelniť s príchodom viacjadrových CPU. Prvé 2D rezy kvoli otestovaniu morfológie HP Chuaovho obvodu, boli počítané pomocou dvojjadrového CPU Intel Core2 6600 s taktovacou frekvenciou 2840 MHz. Niektoré rezy HP ilustruje obr. 2 [2]. Aby bolo možné zobraziť finálnu 3D HP na obr. 3, bolo potrebné celkovo vypočítať 300 rezov. Výpočet jedeného rezu trval približne 5 hodín a tak čas potrebný na výpočet všetkých rezov by bol okolo 1500 hodín! Tým vznikla nutnoť použitia takých prostriedkov, ktoré by umožňovali výraznejšie sparalelniť výpočet rezov HP.

Preto v tomto príspevku poukážeme na možnosti použitia Grid-u a GPGPU, ktoré sú vhodné na takéto výpočty. Na záver tejto časti, pre úplnoť opisu obr. 3 poznamenávame, že vo vnútri HP je žltou farbou vykreslený chaotický atraktor (CHA), ktorý je oddelený od ďalšieho atraktora – stabilného limitého cyklu (SLC) v Chuaovom obvode práve HP. Obr. 4 ilustruje oba atraktory súčasne v projekcii do roviny u1, i [4]. Ich výpočet je však možný len v prípade voľby iných začiatočných podmienok.

Obr. 2 Množina prvých rezov HP v rovine u2, i, ilustrujúca zmenu HP s meniacim sa napätím u1. Jeho veľkosť je uvedená v pravom hornom rohu.. Čierna resp. biela oblasť odpovedá regiónu príťažlivosti chaotického atraktora resp. stabilného limitného cyklu.

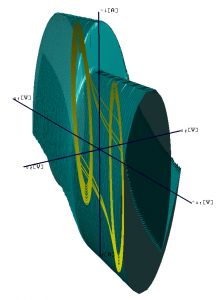
Obr.3 HP oddeľujúca CHA od (nezobrazeného) SLC.

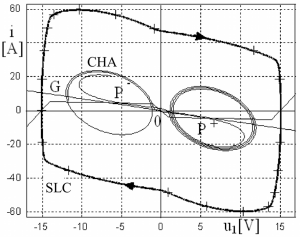
Obr. 4 Projekcia CHA a SLC do roviny u1, i. Symboly P⁺, 0 a P^- označujú tri singularity, ktoré sú všetky nestabilné.

Využitie technológie GRID

S potrebou komplexného zmapovania oblastí príťažlivosti pre jednotlivé atraktory v analyzovaných dynamických systémoch, rástli aj požiadavky na objem výpočtov rezov HP. Ako už bolo v úvode spomenuté, pri požiadavke výpočtu 300 rezov by čas výpočtu pri použití jednoprocesorových počítačov vzrástol až na nemysliteľných 1500 hodín. Vznikla tak jedna veľká úloha, ktorá sa však dala rozdeliť na množinu podúloh, ktoré sú nezávislé od výsledkov ostatných. Podúlohy je teda možné rátať paralelne. Na takéto výpočty sú vhodné Grid technológie.

Pojem Grid sa prvýkrát objavil v septembri 1997 kedy ho Ian Foster a Carl Kesselman použili na označenie novej infraštruktúry pre vedu 21. storočia [5]. Zatiaľčo internetové a webové technológie umožňujú prístup k distribuovaným informáciám [6], Gridové technológie umožňujú prístup k výpočtovým a pamäťovým prostriedkom priestorovo distribuovaným po celom svete. Na Grid možno pozerať ako na nejakú globálnu sieť počítačov, ktoré reprezentujú jedno obrovské výpočtové prostredie. Tým, že poskytuje bezpečné, vysoko – výkonné metódy na prístup k vzdialeným prostriedkom, umožňuje rôznym skupinám, inštitúciám a jednotlivcom, tzv. virtuálnym organizáciám, tieto prostriedky spoločne používať.

Keďže teoreticky je možné rátať aj 300 paralelných podúloh súčasne, celkový výpočet jednej veľkej úlohy by mohol trvať iba 5 hodín. Podúlohy sú v rámci Gridu distribuované na rôzne klastre a v závislosti od počtu klastrov je výpočet jednej úlohy síce dlhší ako 5 hodín, avšak výrazne kratší ako už zmienených 1500 hodín. Pre potreby riešenia úloh prezentovaných v tomto článku boli použité výpočtové zdroje Európskej gridovej infraštruktúry (EGI) [7]. V budúcnosti bude využitá výpočtová kapacita Slovenskej infraštruktúry pre vysokovýkonné počítanie (SIVVP) [8], ktorá po svojom uvedení do prevádzky podstatne zvýši možnosti spracovania výpočtovo náročných úloh.Výsledky výpočtov s využitím Gridu boli publikované napr. v prácach [2], [9] – [12]. V súčasnosti je možné využívať aj tvz. Cloud. Tieto prostriedky zatiaľ na výpočet rezov HP neboli použité.

Využitie technológie GPGPU

V posledných rokoch s rastúcim výkonom grafických kariet, v dôsledku neustále sa zvyšujúceho počtu jadier na grafických kartách, sa uplatňuje aj paralelizácia vedeckých výpočtov. Po roku 2003 bolo možné prostredníctvom GPU realizovať maticové výpočty a s neskorším rozšírením komunikácie s GPU architektúry CUDA z dielne firmy NVIDIA, realizovať paralelné výpočty pomocou GPGPU. Neskorší štandard OpenCL ponúka podporu paralelných výpočtov nielen pre GPU, ale aj pre CPU. 3D HP na obr. 5 pozostávajú zo 100 rezov HP, ktorých výpočet bol realizovaný technológiou GPGPU.

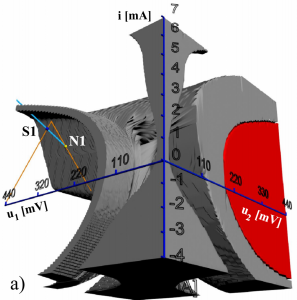
(a)

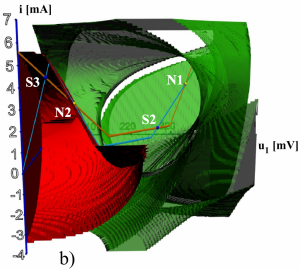
(b)
Obr. 5 Pohľad na 3D modely ternárnej pamäte HP s vynechanou: a) zelenou oblasťou, b) sivou oblasťou príťažlivosti.

Jediná nevýhoda pri využití GPGPU je tá, že väčšina grafických kariet umožňuje výpočty iba s premennými typu float. Drahšie grafické karty či grafické akcelerátory už umožňujú definovať premenné ako double. Ak by išlo o podobné výpočty ako sú ukázané v práci [13] (výpočet stable manifold záporným integračným krokom), tak grafické karty s možnosťou definovania premenných iba typu float by boli nepoužiteľné. Vo väčšine prípadov bežných výpočtov rezov HP je postačujúce použitie premenných typu float. Tab. 1 uvádza porovnanie dĺžky výpočtov rezov HP ternárnej pamäte pomocou PC s využitím jedného CPU a najrýchlejším riešením na báze grafického akcelerátora, ktorý bol testovaný v práci [14].

Aj keď čas výpočtu akcelerátora NVIDIA Tesla C1060 silne závisí od použitej premennej (float alebo double) a čas výpočtu rezu HP pri použití premennej typu double v porovnaní s float je približne 3x dlhší, stále je 24 sekúnd resp. 11 sekúnd pre GPU NVIDIA Tesla C1060, oveľa menej, ako zistené časy výpočtu rezov HP jednotlivých PC, a to v rozmedzí od 15 až do 26x. Pri použití premennej typu float je zrýchlenie ešte väčšie ako 26x (v porovnaní s najrýchlejším AMD Turion II je takmer 60 násobné a s CPU Intel Pentium D dokonca až 100 násobné). Ale aj keby zrýchlenie výpočtov bolo „iba“ 10 násobné, použitie technológie GPGPU je stále zaujímavé a do budúcna perspektívne.

Parametre grafických kariet a spomenutého akcelerátora Tesla umožňujúce výpočty použitím GPGPU, uvádza tab. 2 a grafické porovnanie rýchlosti výpočtu 100 rezov HP ilustuje obr. 6. Je zaujímavé, že pri 10 násobnom zväčšení kapacity C (bližšie informácie o štruktúre a parametroch uvádza prameň [11]) vzrastie na CPU aj dĺžka výpočtov 10 násobne, ale pri použití GPGPU, ako je to zrejmé z obr. 2.2, je to približne iba 5 násobne, čo opäť robí technológiu GPGPU atraktívnou pri tak náročných výpočtoch ako sú rezy HP. Keďže ide o vývojovo najmladšiu technológiu aplikovanú v tejto práci, bola zatiaľ využitá iba v prácach [14] – [17].

Tab. 1 Porovnanie dĺžky výpočtov rezov HP ternárnej pamäte pri použití PC a technológie GPGPU

rovina	hladina	čas [s]
		Intel Pentium D CPU 2.66 GHz (1 GB RAM)		Intel Pentium Dual CPU T3200 2 GHz (3 GB RAM)		AMD Turion II P520 Dual-Core 2,3 GHz (4 GB RAM)		GPU NVIDIA Tesla C1060
		float	double	float	double	float	double	float	double
u2, u1	i = 0.003 A	630	629	507	502	377	365	9	24
u2, i	u1 = 0.22 V	304	303	245	242	181	175	3	11
u1, i	u2 = 0.22 V	292	291	235	233	174	169	3	11

Tab. 2 Parametre použitých grafických kariet

Technické śpecifikácie	GPU
	NVIDIA GeForce 8800 GT	NVIDIA GeForce GT 240	NVIDIA Tesla C1060
CUDA jadrá	112	96	240
procesorový taktovací signál [MHz]	1500	1340	1296
pamäťový taktovací signál [MHz]	900	900	800
štandardná pamäťová konfigurácia [MB]	512	1024	4096
šírka pamäťového rozhrania [bit]	256	128	512
šírka pásma [GB/s]	58	54	102
verzia CUDA Compute capability	1.1	1.2	1.3

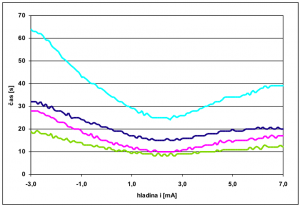
(a)

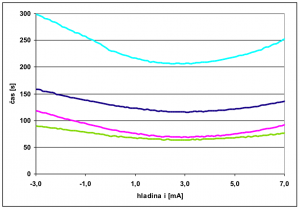
(b)
Obr. 6 Porovnanie rýchlosti výpočtu 100 rezov HP ternárnej pamäte pre rôzne kapacity C = C₁ = C₂ a) C = 2.10^-14 F b) C = 2.10^-13 F.

Záver

Použitím technológií Grid a GPGPU je možné dosiahnuť podstatne väčšiu efektivitu i menšiu časovú náročnosť pri výpočte veľkého počtu 2D rezov HP potrebných na rekonštrukciu trojrozmernej HP, ako iba pri použití jedného viacjadrového PC. Pritom je jedno, či výsledná HP reprezentuje pomery v sekvenčných alebo v chaos generujúcich obvodoch, pretože algoritmus výpočtu 2D rezov je vpodstate ten istý.

Vzhľadom na to, že jeden 2D rez HP použitý v tomto príspevku pozostáva z 440×440 bodov – začiatočných podmienok pre riešenie systému diferenciálnych rovníc, čo predstavuje výpočet takmer 200 000 trajektórií, tak pri požiadavke výpočtu minimálne 100 rezov HP je potrebné vypočítať minimálne 20 miliónov trajektórií, sú výhody využitia oboch technológií nesporné, ak požadujeme výsledky výpočtov v “reálnom” čase.

Poďakovanie

Táto práca bola podporená grantovými projektmi: KEGA č. 005TUKE-4/2012: „Automatizovaný skúšací systém využívajúci moderné informačné technológie“, KEGA č. 050TUKE-4/2012: “Aplikácia technológií virtuálnej reality ako inovačného prostriedku pri výučbe formálnych metód”, VEGA No. 2/0054/12: „Vybrané metódy, prístupy a nástroje pre distribuované spracovanie informácií“ a

Podporujeme výskumné aktivity na Slovensku/ Projekt je spolufinancovaný zo zdrojov EÚ. Tento článok bol vypracovaný v rámci projektu “Centrum excelentnosti integrovaného výskumu a využitia progresívnych materiálov a technológií v oblasti automobilovej elektroniky”, ITMS 26220120055.

Literatúra

1. GUZAN, Milan: Výpočet hraničnej plochy použitím PC. In: Posterus, roč. 5, 2012, č. 9, online:
   http://www.posterus.sk/?p=13713
2. SOBOTA, Branislav – GUZAN, Milan: Rekonštrukcia hraničnej plochy Chuaovho obvodu. In: SEKEL 2010: mezinárodní konference učitelů elektrotechniky: sborník příspěvků z konference: Liberec, Malá Skála, 15. – 17. září 2010, p. 151-156.
3. GUZAN, Milan – SOBOTA, Branislav: Hraničná plocha viac-hodnotovej pamäte v 3D, In: SEKEL 2012, Medzinárodná konferencia učiteľov elektrotechniky, Bratislava, Modra – Harmónia, 5.-7.9.2012, s. 75-80.
4. GUZAN, Milan – GALAJDA, Pavol – PIVKA, Ladislav – ŠPÁNY, Viktor: Element of singularity is a key to laws of chaos. In: RADIOELEKTRONIKA 2005, 15th International Czech-Slovak Scientific Conference, May 2005, p.33-36.
5. Úvodné informácie ku slovenskému EGEE, citované 2012-08-31.
   http://www.ui.sav.sk/egee/intro_sk.php
6. SOBOTA, Branislav – GUZAN, Milan: Vizualizácia nelineárnych dynamických systémov použitím web technológií. In: Nové trendy v prevádzke technických systémov ’09: 9. medzinárodná vedecká konferencia: Prešov, 5.-6.11.2009, s. 89-92.
7. GUZAN, Milan – BUČKO, Radoslav: Morphological Complexity of State Space Quaternary Memory. In: Electrical Engineering and Informatics 2: Proceeding of the Faculty of Electrical Engineering and Informatics of the TU of Košice. Košice: TU, 2011, p. 518-521.
8. Európska gridová infraštruktúra, citované 2012-10-01.
   http://www.egi.eu
9. Slovenská infraštruktúra pre vysokovýkonné počítanie, citované 2012-10-01.
   http://www.sivvp.sk
10. ŠPÁNY, Viktor – GALAJDA, Pavol – GUZAN, Milan – PIVKA, Ladislav – OLEJÁR, Martin: Chua’s singularities: Great miracles in circuit theory. International Journal of Bifurcation and Chaos, vol. 20, 2010, no. 10, p. 2993-3006.
11. GUZAN, Milan: Boundary surface of a ternary memory in the absence of limit cycles In: Radioelektronika 2012: Proceedings of 22nd International Conference: April 17-18, 2012, Brno, Czech Republic, p. 1-4.
12. GUZAN, Milan: Boundary Surface and Limit Cycles of Ternary Memory by Using Forward and Backward Integration. In: EDPE 2011: 17th International Conference on Electrical Drives and Power Electronics: proceedings: 5th Joint Slovak-Croatian Conference: Stará Lesná, High Tatras, 28. – 30. September 2011, Slovakia, s. 171-175.
13. GUZAN, Milan: Boundary surface and stable manifold in sequential circuits. In: Radioelektronika 2011: proceedings of 21th international conference: Brno, University of Technology, April 19-20, 2011, Czech Republic, p. 219-222.
14. ZAVACKÝ, Miroslav: Nelineárne dynamické systémy – riešenie a vizualizácia. Diplomová práca, FEI, TU v Košiciach, 2011, 65 s..
15. GUZAN, Milan – SOBOTA, Branislav: GPGPU Technology in Simulation of Non-linear Dynamic Systems. In: SEKEL 2011: International Conference Czech and Slovak Teachers of Electrical Engineering and Computer Science: Conference proceedings: Horní Lomná, 7. – 9. září 2011, p. 12-14.
16. ZAVACKÝ, Miroslav – GUZAN, Milan – SOBOTA, Branislav: Calculating the boundary surface cuts of multivalued memory. In: SCYR 2011: 11th Scientific Conference of Young Researchers of Faculty of Electrical Engineering and Informatics Technical University of Košice: proceedings from conference, Herľany, May 17th, 2011, s. 256-259.
17. KULKA, Jaroslav.: 3D vizualizácia hraničných plôch polovodičových pamätí, Diplomová práca, FEI, TU v Košiciach, 2012, 60 s.

---

Spoluautormi článku sú doc. Ing. Branislav Sobota, PhD., Katedra počítačov a informatiky, Fakulta elektrotechniky a informatiky, Technická univerzita v Košiciach; Ing. Ján Astaloš, Ústav informatiky, Slovenská akadémia vied, Bratislava