V práci uvádzame jednotný popis pre rôzne sémantiky Petriho sietí. Sémantika, tj. možné správanie, je v podstate množina orientovaných acyklických grafov s označkovanými vrcholmi a hranami. Nazývame ich toky značiek. Vrcholy tokov značiek predstavujú výskyty prechodov z pôvodnej siete, takže sú označkované ako prechody. Hrana medzi výskytom prechodu a výskytom prechodu je označkovaná multimnožinou miest, ktorá vyjadruje kožko značiek vytvorených výskytom prechodu spotrebuje výskyt prechodu .

Začneme krátkym príbehom: K banke prichádza pán J. s manželkou. Pán J. si chce vybrať peniaze z bankomatu, ktorý sa nachádza priamo pri banke a jeho manželka sa ide dnu spýtať na informácie. Pán J. vloží svoju platobnú kartu do bankomatu a zadá príslušný PIN kód, chvíľu čaká a nakoniec si vyberie svoje peniaze. Neznalému pozorovateľovi by sa mohlo zdať, že na výber peňazí z bankomatu je potrebné mať platobnú kartu, zadať PIN kód a poslať dnu do banky ďalšiu osobu, ktorá to tam nahlási. Ako vieme, toto nie je úplne pravda, pretože pán J. si môže vybrať peniaze z bankomatu nezávisle na tom, kedy a či nejaká ďalšia osoba vojde do banky. Ale je pravda, že na výber z bankomatu je potrebné vložiť platobnú kartu do prístroja a zadať PIN.

Pri sekvenčnom zariadení s jedným procesorom nie je potrebné uvažovať o probléme nezávislosti vykonávaných udalostí či akcií. Môžeme si všimnúť nedeterminizmus, napr. zadanie PIN kódu a vojdenie inej osoby do banky sa môžu vykonať v ľubovoľnom poradí. Súbežnosť, paralelnosť (anglicky concurrency) sa podstatne líši od nedeterminizmu, je to nielen možnosť vykonania v ľubovoľnom poradí, ale aj vzájomná nezávislosť. Typickým príkladom, objasňujúcim tento rozdiel, je výskyt dvoch udalostí (napr. dve osoby, ktoré si chcú vybrať peniaze z bankomatu) zdieľajúcich jeden zdroj (bankomat). Tieto dve udalosti sa môžu stať v ľubovoľnom poradí, ale nemôžu nastať súčasne. Dalo by sa povedať, že súbežnosť zahŕňa výskyt v ľubovoľnom poradí a súčasného výskytu.

Uvedený príklad taktiež ukazuje, že súbežnosť je nielen súčasný výskyt, ktorý je tranzitívny: iná osoba môže vojsť do banky súčasne s vložením platobnej karty (pán J.) do bankomatu a/alebo súčasne so zadaním PIN kódu (pán J.). No vloženie platobnej karty a zadanie PIN kódu sa nemôžu vykonať súčasne, ale sú kauzálne závislé. Vidíme, že udalosť zadanie PIN kódu kauzálne závisí od udalosti vloženie platobnej karty, ale môžeme uskutočniť viac výberov a zadať PIN kód viac krát. Ak povieme, že vloženie platobnej karty je udalosť a zadanie PIN kódu iná udalosť, hovoríme o kauzálnej závislosti medzi výskytmi udalostí, a nie ako o kauzálnej závislosti medzi udalosťami samotnými.

V posledných rokoch sa dostalo viac pozornosti štúdiu súbežnosti, ako javu správania sa systémov, kvôli narastajúcemu počtu distribuovaných systémov, viacprocesorových systémov a komunikačných sietí, ktoré sú už vo svojej podstate paralelné. V literatúre existuje veľa spôsobov na popis nesekvenčného správanie, väčšina z nich je založená na orientovaných acyklických grafoch (directed acyclic graphs – DAGs). Zvyčajne vrcholy týchto grafov (DAG-ov) reprezentujú výskyty udalostí, t.j. sú označené množinou udalostí a označkované grafy (labelled DAGs – LDAGs) sú zhodné až na izomorfizmus. Takéto LDAG-y sú uvedené v literatúre ako abstrakt [30]. Veľmi často sú používané LDAG-y s tranzitívnymi hranami, t.j. čiastočné usporiadanie. Tieto konštrukcie sú označované ako čiastočne usporiadané multimnožiny, skrátene pomsets (partially ordered multisets), a formálne ich možno považovať za izomorfné triedy s označkovanými čiastočnými usporiadaniami [29]. Pomset-y sa tiež nazývajú čiastočné slová [19], s dôrazom na ich blízky vzťah k slovám alebo sekvenciám, úplné usporiadanie prvkov v sekvencii je nahradené čiastočným usporiadaním.

Petriho siete prvý krát popísal vo svojej dizertačnej práci Carl Adam Petri v roku 1962. Na Slovensku majú tiež dlhú históriu. Už v roku 1985 sa nimi zaoberal Čičák (FIIT STU Bratislava) [4] – [8], [12] – [14], [26], neskôr Čapkovič (SAV Bratislava) [9, 10, 34], Hudák (FEI TU Košice) [28, 33], ale aj iní mladí vedci, celosvetovo významný Juhás (FEI STU Bratislava) [15, 20, 21, 23], Žarnay (FRI Žilina) [35, 36]. Petriho siete sú jedným z najvýznamnejších formalizmov pre pochopenie súbežnosti na teoretickej aj abstraktnej úrovni, ako aj pre modelovanie reálnych paralelných systémov v rôznych oblastiach využitia. Existuje na to veľa dôvodov, okrem iného kombinácia grafickej zrozumiteľnosti a matematického popisu, pozri napr. [15] pre viac informácií.

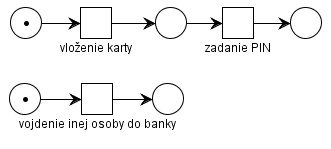
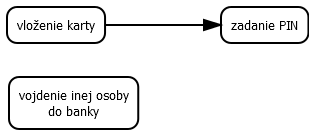
Obrazok 1.1 Petriho sieť predstavujúca príbeh z úvodu (nahor). Na popísanie nezávislej relácie potrebujeme aspoň dve krokové postupnosti: postupnosť s krokom vloženie karty a vojdenie inej osoby do banky za ktorým nasleduje krok zadanie PIN a postupnosť s krokom vloženie karty za ktorým nasleduje krok vojdenie inej osoby do banky a zadanie PIN. Zodpovedajúce čiastočné usporiadanie (pomset) daného správania (nadol).

Petriho sieť (place/transition Petri net) pozostáva z množiny prechodov (udalostí, angl. transition), ktoré sa môžu vykonať (spustiť) a množiny miest (zásobníky značiek, angl. place), ktoré môžu obsahovať niekoľko značiek (angl. token). Rozdelenie značiek v miestach predstavuje stav Petriho siete, označuje sa značkovanie. Formálne, značkovanie je dané multimnožinou miest, t.j. funkciou priraďujúcou každému miestu počet značiek, ktoré sa nachádzajú v danom mieste. Vykonanie prechodu v aktuálnom značkovaní odstráni určený (pevne daný) počet značiek z miest, t.j. spotrebuje multimnožinu z miest, z ktorých vedú hrany do daného prechodu a pridá určený (pevne daný) počet značiek do miest, t.j. vytvorí multimnožinu do miest, kam vedú hrany z daného prechodu, vedie to k novému značkovaniu. Prechod je spustiteľný v značkovaní, ak existuje dostatočný počet značiek, ktoré majú byť spotrebované spustením prechodu. V práci budú výskyty prechodov označované ako udalosti. Taktiež budeme uvažovať pevne dané počiatočné značkovanie a množinu prípustných konečných značkovaní.

Existuje veľa rôznych spôsobov ako definovať správanie Petriho sietí. Najjednoduchšie je zaoberať sa spustiteľnými sekvenciami, t.j. sekvenciami spustiteľných prechodov. Ďalšou možnosťou je rozšíriť sekvencie spustiteľných prechodov na krokové sekvencie prechodov (step sekvencie). Kroky sú multimnožiny prechodov. Krok je v značkovaní spustiteľný, ak existuje dostatočný počet značiek, ktoré majú byť spotrebované súčasným spustením všetkých prechodov z multimnožiny. Situácia opísaná v úvodnom príklade, kde nezávislosť výskytu prechodov nie je tranzitívna, nemôže byť popísaná jednoduchou krokovou sekvenciou, viď. obrázok 1.1.

Z tohto dôvodu sa pomsety zdajú byť lepšou voľbou ako formalizovať nesekvenčné sémantiky (viď. napr. [29, 19]). Vynára sa prirodzená otázka: ktoré pomsety vyjadrujú správanie Petriho sietí? Odpoveďou je kroková sémantika. V [19, 22] je navrhnuté, aby pomsety spĺňali: Pre každú podmnožinu udalostí (t.j. pre každú množinu neusporiadaných udalostí, angl. co-set) musí platiť: Krok udalostí v podmnožine je spustiteľný, v značkovaní dosiahnuteľnom z počiatočného značkovania, ak sa dajú spustiť všetky udalosti, ktoré predchádzajú udalostiam z podmnožiny.

Ďalšou možnosťou ako vyjadriť správanie Petriho sietí je pomocou procesov z [17, 18], ktoré sú špeciálnym druhom acyklických sietí, tzv. siete spustení alebo výskytov udalostí (angl. occurrence nets), spolu so značkovaním, ktoré miestam (nazývané stavy, angl. condition) a prechodom (nazývané javy, udalosti, angl. event) zo sietí výskytov priraďuje miesta a prechody originálnych Petriho sietí, zachovávajúcim počet spotrebovaných a vytvorených značiek, viď. obrázok 1.2. Procesy môžu byť chápané ako (nerozvetvené) rozvinutia pôvodných sietí: každý stav v procese predstavuje výskyt jeho označenia v pôvodnej sieti.

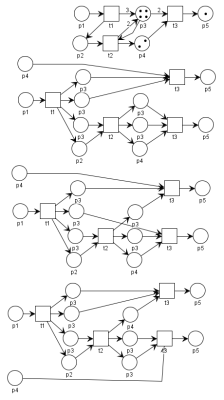
Obrazok 1.2 Petriho sieť (hore) s tromi procesmi (nižšie).

Odhliadnuc od stavov v procesných sieťach, máme definované LDAG-y udalostí. Tieto LDAG-y vyjadrujú priamu závislosť medzi udalosťami. Pridaním tranzitívnych hrán do LDAG-ov dostaneme pomsety nazývané behy (angl. run), ktoré vyjadrujú (nie nutne priamu) závislosť medzi udalosťami. Na rozdiel od prípustných pomsetov, udalosti pospájané hranami v behu nemôžu byť nezávislé. Osobitú úlohu zohrávajú behy, ktoré sú minimálne vzhľadom na rozšírenie: vyjadrujú minimálnu závislosť medzi udalosťami. Dôležitý výsledok vzťahu medzi prípustnými pomsetmi a behmi bol dokázaný v [22, 31]: Každý prípustný pomset obsahuje beh a každý beh je prípustný pomset. Preto, minimálny prípustný pomset je rovný minimálnemu behu. Na rozdiel od sekvenčnej a krokovej sémantiky, procesy rozlišujú medzi históriou značiek, t.j. ktoré udalosti jednotlivé značky vyprodukovali a ktoré udalosti ich spotrebujú. Príklad je zobrazený na obrázku 1.2.

Procesné siete rozlišujú značku v mieste vyprodukovanú prechodom a značku v mieste vyprodukovanú prechodom . Dôsledkom toho jedna sekvencia výskytov udalostí, napr. , môže byť rozšírením dvoch rôznych procesov. Procesná sémantika definovaná v [17] sa taktiež nazýva individuálna značková sémantika (angl. individual token semantics). Všimnime si, že v prípade procesnej sémantiky elementárnej siete (s najviac jednou značkou v mieste), každá sekvencia výskytov a každá kroková sekvencia jednoznačne určujú proces. V [3] je uvedená hromadná značková sémantika (angl. collective token semantics), ktorá nerozlišuje medzi históriou značiek. Je definovaná pomocou relácie ekvivalencie medzi procesmi. Relácia ekvivalencie procesov sa líši iba v permutáciách (zámene, angl. swapping) neusporiadaných stavov, reprezentujúcich značky na rovnakých miestach v pôvodnej sieti. Napríklad procesy na obrázku 1.2 sú ekvivalentné, s ohľadom na zámennú (permutačnú) ekvivalenciu. Pre triedy zámenných ekvivalencií, nazývaných komutatívne procesy, platí, že každá sekvencia výskytov a každá kroková sekvencia jednoznačne určuje komutatívny proces.

V [25] je správanie popísané pomocou prepisovacích termov generovaných zo základných elementárnych termov pomocou paralelného a sekvenčného skladania. V tomto algebraickom prístupe je každý prechod elementárnym prepisovacím termom, umožňujúcim nahradiť značkovanie značkovaním . Ľubovoľné značkovanie obsahujúce jediné miesto je elementárny term, prepisujúci samým sebou. Prepisujúce termy sú induktívne vytvorené z elementárnych termov použitím operátora pre sekvenčné a operátora pre paralelné skladanie. Ku každému termu je pripojené počiatočné a koncové značkovanie. Dva termy môžu byť zložené len vtedy, ak je koncové značkovanie prvého termu zhodné s~počiatočným značkovaním druhého termu. Pre paralelné zloženie dvoch termov, počiatočné značkovanie výsledného (zloženého) termu dostaneme sčítaním počiatočných značkovaní skladaných termov, podobne to platí aj pre koncové značkovanie.

Správanie siete je dané triedami ekvivalencií prepisovacích termov definovaných súborom rovníc. V [11] je ukázané, že trieda ekvivalencie prepisovacích termov, ako sú definované v [25], sa zhoduje s triedou zámennej ekvivalencie procesov. Je zrejmé, že pomsety môžeme prepojiť s prepisovacími termami. Každý procesný term definuje čiastočne usporiadanú množinu udalostí reprezentujúcu výskyty prechodov nasledujúco: udalosť je menšia ako udalosť , ak prepisovací term obsahuje podterm tak, že prislúcha k a prislúcha k . Pomset prepisovacích termov má špeciálnu štruktúru. V [16] je dokázané, že pomset je vytvorený paralelným a sekvenčným skladaním jednoduchých prvkov pomsetu práve vtedy, keď neobsahujú takzvanú N-formu. Ako dôsledok dostaneme charakteristiku pomsetov, ktoré sú asociované s prepisovacími termami Petriho sietí: prípustný pomset je asociovaný s prepisovacím termom siete práve vtedy, keď je N-free (budeme používať tento anglický pojem).

Väčšina zo spomenutých výsledkov ukazuje, že prechody medzi rôznymi sémantikami sú celkom komplikované, napriek jasnej intuícii. Rozdielne techniky použité na popis správania často spôsobujú, že aj jasné vzájomné vzťahy majú technicky ťažké dôkazy. Formálny intuitívny popis, zvolený pre jednoduchú sémantiku, má svoje obmedzenia. Zoberme si napríklad prípustné pomsety a procesy. Definícia prípustných pomsetov je určite exponenciálna: je neefektívne použiť podmnožiny (co-sety) a kroky na testovanie prípustnosti. Hlavnou výhodou procesov, ako tvrdí literatúra, je popis správania rovnakým modelovacím jazykom, t.j. používajú sieť výskytov udalostí. Zároveň je to aj ich hlavná nevýhoda, pretože namodelovanie každej jednej značky samostatnou podmienkou spraví formálne pracovanie s procesmi ťažkým. V skutočnosti si nepotrebujeme pamätať každú jednu značku (je to vhodné pre elementárne siete, kde každé miesto v značkovaní obsahuje najviac jednu značku, ale nie je to také užitočné v (place/transition) Petriho sieťach). Je dobré si pamätať, koľko značiek vytvorených spustením bude spotrebovaných iným spustením, t.j. koľko značiek pretečie hranou spájajúcou výskyty prechodov, odhliadnuc od jednotlivých podmienok.

Vzniká prirodzená otázka, či existuje možnosť vyjadriť všetky doteraz spomínané sémantiky použitím jednotného a zároveň jednoduchého formalizmu. Na túto otázku existuje kladná odpoveď, predstavíme konštrukciu pre popis rôznych variantov sémantiky Petriho sietí. Kostra sémantiky je v podstate množina orientovaných acyklických grafov s označkovanými vrcholmi a hranami, nazývané tok značiek (angl. token flow), kde grafy sú zhodné až na izomorfizmus, pôvodne definované v [20]. Vrcholy grafu predstavujúceho tok značiek reprezentujú výskyty prechodov základnej (pôvodnej) siete, preto sú označené ako prechody. Hrany sú označené multimnožinami miest. Konkrétne, hrana medzi výskytom prechodu a výskytom prechodu je označená multimnožinou miest, vyjadrujúca koľko značiek vytvorených výskytom prechodu $ latex a$ spotrebuje výskyt prechodu . Tok značiek Petriho siete musí spĺňať takzvané vlastnosti toku značiek:

• vchádzajúci tok značiek (t.j. súčet multimnožín vstupných hrán) každého výskytu prechodu je rovný multimnožine miest spotrebovaných v sieti spustením prechodu
• vychádzajúci tok značiek (t.j. súčet multimnožín výstupných hrán) každého výskytu prechodu je rovný multimnožine miest vytvorených v sieti spustením prechodu

Na zachovanie informácie, ktoré výskyty spotrebujú značky priamo z počiatočného značkovania a ktoré výskyty vytvoria nespotrebované značky v konečnom značkovaní, pridáme špeciálny (jediný) vstupný vrchol (vstup) a špeciálny (jediný) výstupný vrchol (výstup). Tieto vrcholy sú označené počiatočným a konečným značkovaním, v tomto poradí. Vychádzajúci tok značiek vstupu je rovný počiatočnému značkovaniu a vstupný tok značiek výstupu je rovný konečnému značkovaniu. Keď vyjadríme správanie pomocou množiny LDAG, tj. pomocou jazyka LDAG, vyplynie dôležitá otázka: Aká je interpretácia hrán v LDAG? Odpoveď nie je jednoznačná. Použitím Petriho sietí nájdeme dve základné interpretácie:

1. Výskyt udalosti \textit{priamo kauzálne závisí} na výskyte udalosti : Vykonaním prechodu , prechod spotrebuje niektoré značky vytvorené výskytom udalosti . táto interpretácia je použitá pri procesoch Petriho sietí [17, 18]. Priamo kauzálna interpretácia hrán je dôsledkom požiadavky, aby bol nenulový tok značiek medzi výskytmi, tj. množina označení nejakej hrany nie je rovná prázdnej množine. Tranzitívny uzáver priamej kauzality dáva kauzálnu závislosť.
2. Výskyt udalosti nasleduje po výskyte udalosti : Výskyt udalosti je buď kauzálne závislý na výskyte , alebo výskyty a sú nezávislé. Takáto interpretácia je použitá pri sekvenciách výskytov, krokových sekvenciách a prípustných pomsetoch Petriho sietí [19]. Túto interpretáciu nazývame interpretácia výskytov. Pri interpretácii výskytov sú povolené aj hrany s nulovým tokom značiek.

Rôzne varianty správania Petriho siete sú dané odlišnou interpretáciou hrán a odlišnou štruktúrou grafov reprezentujúcich tok značiek, čo vedie k rozdielnym množinám označkovaných orientovaných acyklických grafov prípustných v sieti. Uvedieme, že najvýznamnejšia sémantika Petriho sietí zodpovedá rôznym podmnožinám tokov značiek. A to:

• Procesy Goltza a Reisiga [17, 18] zodpovedajú priamym kauzálnym tokom značiek (angl. direct causal token flows), t.j. tok značiek s priamo kauzálnou interpretáciou hrán, kde všetky hrany majú nenulový tok značiek.
• Toky značiek, v ktorých LDAGy sú pomsety a aspoň kostrové hrany (netranzitívne hrany) majú nenulový tok značiek, sa nazývajú kauzálne toky značiek (angl. causal token flows) Petriho sietí a predstavujú kauzálnu sémantiku. Vznikajú z priamych kauzálnych tokov značiek pridaním všetkých tranzitívnych hrán.
• Prípustné pomsety, tj. čiastočné slová zavedené Grabowskim [19], zodpovedajú pomset tokom značiek (angl. partially ordered multiset token flows), t.j. tokom značiek, kde LDAGy sú pomsety s interpretáciou výskytov hrán (hrany môžu mať nulový tok značiek).
• Prepisovacie termy Meseguera a Montanariho [25] zodpovedajú N-free tokom značiek (angl. N-free token flows), t.j. pomset toku značiek, kde pôvodné pomsety sú N-free.
• Krokové sekvencie zodpovedajú krokovo usporiadaným multimnožinám tokov značiek, skrátene somset toky značiek (angl. step ordered multiset token flows), t.j. zodpovedajú pomset tokom značiek, kde relácia daná neusporiadanými dvojicami vrcholov je tranzitívna.
• Sekvencie výskytov udalostí zodpovedajú úplne usporiadaným tokom značiek, skrátene {\em tomset toky značiek} (angl. totally ordered multiset token flows), t.j. zodpovedajú pomsetom, kde relácia daná neusporiadanými dvojicami vrcholov je prázdna.

Pre lepšiu predstavu, priame kauzálne toky značiek zodpovedajúce procesom z obrázku 1.2 sú znázornené na obrázku 1.3.

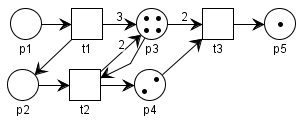
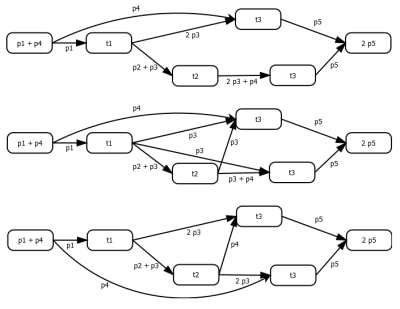
Obrazok 1.3 Petriho sieť z obrázku 1.2 (hore) a priame kauzálne toky značiek zodpovedajúce procesom z obrázku 1.2.

Dôležitú úlohu zohráva ekvivalencia daná symetrickým a tranzitívnym uzáverom relácie rozšírenia LDAGov, nazývaná ekvivalencia rozšírenia (angl. extension equivalence). Triedy ekvivalencie, dané výmennou ekvivalenciou sekvencií (angl. exchange equivalence), zámennou ekvivalenciou procesov (angl. swapping equivalence), a ekvivalenciou prepisovacích termov, zodpovedajú obmedzeniu tried výmennej ekvivalencie na tomset toky značiek, priamo kauzálne toky značiek a~N-free toky značiek, v tomto poradí.

Literatúra

1. Bergenthum, R., Lorenz, R., Mauser, S.: Faster Unfolding of General Petri Nets Based on Token Flows. In: Petri Nets 2008. LNCS, vol. 5062, pp. 13–32. Springer, Heidelberg (2008)
2. Bergenthum, Desel, J., Lorenz, R., Mauser, S.: Synthesis of Petri Nets from Finite Partial Languages. Fundamenta Informaticae 88(4), 437–468 (2008)
3. Best, E., Devillers, R.: Sequential and Concurrent Behaviour in Petri Net Theory. Theoretical Computer Science 55(1), 87–136 (1987)
4. Čičák, P.: Microprogram Modification of Petri Nets. In: 39.Internationales Wissenschaftliches Kolloquium, 27.-30.9.1994, Band 1 Vortragsreihen Anwendungen von Petri-Netzen, s. 560-564 (1994)
5. Čičák, P.: Microprogram Petri Nets and Their Utilization. In: Microsystém ’89, 1989, České Budějovice, s. 87 – 91 (1989)
6. Čičák, P.: The use of Microprogram Petri Nets in the Microprogram Control systems Modelling. In MOSIS 98 : Modelling and Simulation of Systems, Proceedings of the Conference, Volume 2: Konf. Sv.Hostýn-Bystřice pod Hostýnem, May 5-7,1998, Ostrava: MARQ, 1998, s. 31–38, ISBN 80-85988-24-0 (1998)
7. Čičák, P.: Základné pojmy a vlastnosti Petriho sietí. Elektrotechnický časopis. Vol. 36, 1985, č. 1, s. 80 – 85 (1985)
8. Čičák, P., Mostafa, H. E.: Petri-Nets Manipulation to Reduce Roaming Duration: Criterion to Improve Handoff Management. In: Transactions on Engineering, Computing and Technology, Canakkale, Turkey: World Enformatika Society, ISSN 1305-5313, Vol. 12 (2006), s. 182-187 (2006)
9. Čapkovič, F.: Petri Nets-Based Computer Aided Synthesis of Control Systems for Discrete Events Dynamic Systems. In Preprint of the 5-th IFAC/IMACS Symposium on Computer Aided Design in Control Systems ’91, s. 409-414 (1991)
10. Čapkovič, F., Čapkovič, P.: Petri net-based automated control synthesis for a class of DEDS. In ETFA 2003. – IEEE, s. 297-304 (2003)
11. Degano, E., Meseguer, J., and Montanari, U.: Axiomatizing the Algebra of Net Computations and Processes. Acta Informatica 33(7), 641–667 (1996)
12. Ďuďák, J., Čičák, P.: Communication Protocols Models by coloured Petri Nets. Trenčianske Teplice, Mechatronika 2009, Jún 3 – 5 2009, In: Proceedings of 12th international conference on Mechatronics, Trenčín, Jún 3. – 5. 2009, 200 s., pp. 109 – 115, ISBN 978-80-8075-392-4 (2009)
13. Ďuďák, J., Čičák, P.: Model manažovania spojení v TCP protokole pomocou farebných Petriho sietí. Tatranské Zruby, Október 14-16 2009, In: Komunikačné a informačné technológie: 5. vedecká konferencia s medzinárodnou účasou. Liptovský Mikuláš: AOS, 2009, ISBN 978-80-8040-376-8, [6 s.] (2009)
14. Ďuďák, J., Čičák, P.: Model of the Modbus Protocol Using Coloured Petri Nets. Olomouc, Október 20-22. In: Advanced Simulation of Systems: Proceedings of the 31st International Autumn Colloquium, Ostrava: MARQ, 2009, ISBN 978-80-86840-47-5, p.121-126 (2009)
15. Desel, J., Juhás, G.: What is a Petri Net? Informal Answers for the Informed Readers. In: Unifying Petri Nets, Advances in Petri Nets. LNCS, vol. 2128, pp. 1-25. Springer, Heidelberg (2001)
16. Gischer, J.L.: The equational theory of pomsets. Theoretical Computer Science 61(2-3), 199-224 (1988)
17. Goltz, U. and Reisig, W.: The Non-Sequential Behaviour of Petri Nets. Information and Control 57(2-3), 125-147 (1983)
18. Goltz, U. and Reisig, W.: Processes of Place/Transition Nets. In: ICALP’83. LNCS, vol. 154, pp. 264–277. Springer, Heidelberg (1983)
19. Grabowski, J.: On Partial Languages. Fundamenta Informaticae 4(2), 428–498 (1981)
20. Juhás, G.: Are these events independent? It depends! Habilitation thesis, Katholic University Eichstatt-Ingolstadt (2005)
21. Juhás, G., Lorenz, R., Desel, J.: Can I Execute my Scenario in Your Net? In: ICATPN 2005. LNCS, vol. 3536, pp. 289–308. Springer, Heidelberg (2005)
22. Kiehn, A.: On the Interrelationship between Synchronized and Non-Synchronized Behavior of Petri Nets. Journal Inf. Process. Cybern. EIK 24(1-2), 3–18 (1988)
23. Lorenz, R., Juhás, G.: Toward Synthesis of Petri Nets from Scenarios. In: ICATPN 2006. LNCS, vol. 4024, pp. 302–321. Springer, Heidelberg (2006)
24. Lorenz, R., Juhás, G., Bergenthum, R., Desel, J., Mauser, S.: Executability of scenarios in Petri nets. Theoretical Computer Science 410(12-13), 1190–1216 (2009)
25. Meseguer, J., Montanari, U.: Petri nets are monoids. Information and Computation 88(2), 105–155 (1990)
26. Mostafa, H. E., Čičák, P.: Hands on Roaming Duration: Petri-Nets Modelling of a Wireless Mobile-IP Procedure in Cisco Platform. In: International Conference on Networking and Services, IEEE / Cisco ICNS 2006 International Conference Proceedings, July 16-19 2006, Silicon Valley, Marriott Hotel, Santa Clara, California, USA, ISBN 0-7695-2622-5 (2006)
27. Oliveira, M.: Hasse Diagram Generators and Petri Nets. In: Petri Nets 2009. LNCS. Springer, Heidelberg (to appear, 2009)
28. Peko, I., Hudák, Š.: General composition for high level Petri nets and its properties. In: Central European Journal of Computer Science, Vol. 2, no. 3 (2012), p. 222-235, ISSN 2081-9935 (2012)
29. Pratt, V.: Modelling Concurrency with Partial Orders. Int. Journal of Parallel Programming 15(1), 33–71 (1986)
30. Priese, L.: Semi-rational sets of dags. In: DLT 2005. LNCS, vol. 3572, pp. 385–396. Springer, Heildelberg (2005)
31. Vogler, W.: Partial words versus processes: a short comparison.
    In: Advances in Petri Nets. LNCS, vol. 609, pp. 292-303. Springer, Heidelberg (1992)
32. Schrijver, A.: Theory of linear and integer programming. Wiley, Chichester (1986)
33. ŠŠimoňák S., Hudák Š.: Using Petri Nets and Process Algebra in FDT Interfacing. The Fifth International Scientific Conference Electronics Computers and Informatics´2002, 10.-11.10.2002, Košice – Heržany, 2002, pp. 8-13, 80-7099-879-2 (2002)
34. Tzafestas, S.G., Čapkovič, F.: Petri net-based approach to synthesis of intelligent control systems for DEDS. In Computer-assisted management and control of manufacturing systems, Berlin-Heidelberg-New York: Springer Verlag, 1997, chapter 12, p. 325-351, ISBN 3-540-76110-1 (1997)
35. Žarnay, M., Marek, J.: Comparing versions of banker’s algorithm for deadlock avoidance in resource allocation systems, in Formal Methods for Automation and Safety in Railway and Automotive Systems. Proceedings of 9th Symposium FORMS/FORMAT 2012, E. Schnieder, G. Tarnai, (Eds.), Braunschweig (Germany), December 2012, pp. 262-272, ISBN 978-3-9803363-3-8 (2012)
36. Žarnay, M., Silva, M.: Decolourisation of stochastic symmetric nets with bags. In 2010 IEEE International Conference on Systems, Man and Cybernetics, Istanbul (Turkey), October 2010, ISBN 978-1-4244-6587-3 (2010)