Zmena vzorkovacej frekvencie s ľubovoľným faktorm

13. August, 2014, Autor článku: Jacko Martin, Elektrotechnika
Ročník 7, číslo 8 Pridať príspevok

p17273_icon Článok sa venuje zmene vzorkovacej frekvencie f_x vstupného diskrétneho signálu s ľubovoľným faktorom. Výsledkom je výstupný diskrétny signál s novou vzorkovacou frekvenciou f_y. Zmena vzorkovacej frekvencie sa dosiahneme použitím metódy číslicového spracovania signálov známej vo všeobecnosti ako interpolácia. Pre výpočet interpolovanej vzorky v danom časovom okamžiku sa pritom používa len niekoľko vzoriek vstupného diskrétneho signálu z blízkeho okolia tohto okamžiku.

Vykonali sme prevzorkovanie vstupného diskrétneho signálu interpolačnými metódami pomocou kubického splajnu definovaného v Matlabe funkciou spline, ďalej pomocou Lagrangeových polynómov tretieho stupňa a Farrowovej štruktúry. Pre vyhodnotenie presnosti prevzorkovania sme vypočítali strednú kvadratickú chybu. Vo všeobecnosti je tento prístup použiteľný, keď pomer f_x/f_y je racionálne, alebo iracionálne číslo a je vhodný pre zvýšenie ako aj zníženie vzorkovacej frekvencie.

1. Úvod

Mnoho diskrétnych systémov so zmenou vzorkovacej frekvencie našlo svoje uplatnenie medzi modernými algoritmami pre číslicové spracovanie signálov vzhľadom k svojej vysokej výpočtovej efektívnosti zvlášť v spojení s implementáciou na signálovom procesore. Takéto systémy pracujúce s viacerými vzorkovacími frekvenciami sú známe ako mnohorýchlostné systémy [1-5]. Svoje uplatnenie nachádzajú v mnohých oblastiach ako sú komunikačné systémy, spracovanie reči, simulácia akustiky miestnosti využívajúca wavelety, kompresia obrazu, anténne systémy, radarové systémy, systémy utajovania hovorov, transmultiplexory, senzorové systémy, modely pre návrh architektúry mikroelektronických obvodov atď. [6].

Typickým príkladom využitia zmeny vzorkovacej frekvencie je konverzia hudobných záznamov, spracovaných v hudobných štúdiách (vzorkovacia frekvencia býva f_v=48 [kHz] alebo f_v=96 [kHz] a ich ukladanie na kompaktný disk (CD), kde sa používa vzorkovacia frekvencia f_v=44,1 [kHz]. Riešenie by mohlo byť zdánlivo jednoduché. Digitálny záznam by sme previedli spätne na analógový signál a ten by sme potom znovu vzorkovali s novou vzokovacou frekvenciou. Pri analógovo číslicovom (A/Č) a číslicovo analógovom (Č/A) prevode môžu byť zavedené také závažné chyby a rušenia, že po vykonaní tohoto postupu je výsledný signál takmer nepoužiteľný. Ďaleko výhodnejšie je zmeniť vzorkovaciu frekvenciu priamo u diskrétneho alebo číslicového signálu.

2. Interpolácia v časovej oblasti

Nové hodnoty vzoriek môžu byť vypočítané v ľubovoľných časových okamžikoch využitím metódy číslicového spracovania signálu, techniky známej všeobecne ako interpolácia. Filter realizujúci túto interpoláciu sa jednoducho nazýva interpolátor [7]. Na interpoláciu s ľubovoľným faktorom sa môžeme pozerať ako na výpočet nových vzoriek v ľubovoľných bodoch (časových okamžikoch) medzi existujúcimi vzorkami. Koncepcia je uvedená na obr.1. Vstupná postupnosť …, x((n_ℓ -2)T_x), x((n_ℓ -1)T_x), x(n_ℓ T_x), x((n_ℓ +1)T_x), x((n_ℓ+2)T_x), … je vytvorená z rovnomerne rozložených vzoriek so vzorkovacou periódou . Nová vzorka y(ℓT_y), nazývaná interpolant sa nachádza v bode ℓT_y=n_ℓT_y+μ_ℓT_x medzi vzorkami x(n_ℓT_x) a x((n_ℓ+1)T_x). Index vstupnej vzorky n_ℓ sa nazýva základný index a μ_ℓ index zlomkového intervalu.

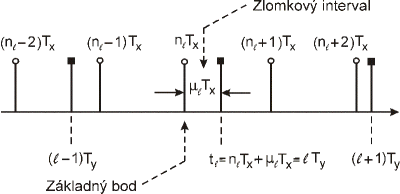
Obr. 1 Vzťahy medzi vstupnou postupnosťou a interpolovanou postupnosťou v časovej oblasti, krúžok – vstupné vzorky, štvorec – výstupné vzorky.

Index vstupnej vzorky n_ℓ sa nazýva základný index a μ_ℓ index zlomkového intervalu, ktorý môže nadobudnúť ľubovoľnú hodnotu v rozsahu 0 ≤ μ_ℓ < 1. Nová hodnota vzorky y(ℓT_y) sa vypočíta z existujúcich vzoriek použitím interpolačného algoritmu. Na obr.2 môžeme vidieť algotitmus interpolácie. Pre daný vstupný signálu x(n), výstupná vzorka y[ℓ] sa vypočíta použitím interpolačného algoritmu pre index vstupnej vzorky n_ℓ a pre index zlomkového intervalu μ_ℓ. Interpolačný algoritmus môžeme definovať ako časovo premenný číslicový filter s impulznou odozvou h(nℓ, μℓ). Nová vzorka y(tℓ)=y(ℓTy) je umiestnená medzi vstupnými vzorkami x(n_ℓT_x) a x((n_ℓ+1)T_x) v čase t_ℓ, ktorú vyjadríme pomocou vstupnej vzorkovacej periódy Tx, indexu vstupnej vzorky n_ℓ a indexu zlomkového intervalu μ_ℓ, ako to vidno na obr.1.

$t_{\iota} = (n_{\iota} + \mu_{\iota})T_x$

(1)

Pre časový okamžik μ_ℓ je index vstupnej vzorky n_ℓ určený takto

$n_{\iota} = [t_{\iota} / T_x]$

(2)

a index zlomkového intervalu

$\mu_{\iota} = t_{\iota} / T_x - [t_{\iota} / T_x]$

(3)

kde [x] predstavuje celočíselnú časť z x. Uvažujme postupnosť x(n) ako diskrétny signál získaný vzorkovaním spojitého signálu x_c(t) s frekvenčne ohraničeným spektrom, ktorého vzorkovacia perióda je T_x

$x[n] = x_c(nT_x)$

(4)

Ideálnu interpoláciu si môžeme predstaviť ako vzorkovanie x_c(t) v časovom okamžiku t_ℓ, z čoho vlastne dostaneme interpolant y[ℓ]= x_c(t_ℓ). Pre dosiahnutie predpokladaného ideálneho prípadu je potrebné ideálne obnoviť spojitý signál x_c(t) zo vzoriek x(n) a prevzorkovať obnovený signál v časovom okamžiku t_ℓ. V skutočnosti generujeme aproximovaný signál y_c(t) a určíme interpolant y[ℓ] pomocou vzorkovania y_c(t) v časovom okamžiku t_ℓ [8]

$y[ \iota ] = y_c(t_{\iota }) = y_c((n_{\iota } + \mu_{\iota })T_x)$

(5)

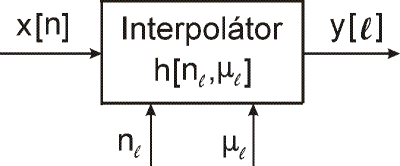
Obr. 2 Zjednodušený model všeobecného interpolátora.

Z toho dôvodu, problém interpolácie môže byť považovaný ako problém rekonštrukcie. V skutočnosti používame interpolačný algoritmus na vytvorenie časovo spojitého signálu y_c(t) z konečného počtu egzistujúcich vzoriek x[n]. Použijeme interval N=N₂+N₁+1 po sebe idúcich vzoriek v okolí vzorky s indexom vstupnej vzorky takým spôsobom, že – N₁+n_ℓ ≤ n_ℓ ≤ n_ℓ+N₂. Zvyčajne používané interpolačné metódy sú založené na polynomiálnych aproximáciách. V tomto prípade pre postupnosť vstupných vzoriek {x[-N₁+n_ℓ], … ,x[n_ℓ], … , x[n_ℓ+N₂]}, je polynomiálna aproximácia y_c(t) signálu x_c(t) definovaná takto

$y_c (t) = \sum_{k=-N_1}^{N_2} P_k (t) (n_{\iota } +k)$

(6)

kde P_k(t) sú polynómy. Vo väčšine aplikácií sa používajú dva všeobecné druhy polynómov: Lagrangeove polynómy a B-splajnové funkcie. Ďalej ukážeme proces interpolácie na základe Lagrangeových polynómov. Lagrangeove polynómy P_k(t) sú dané vzťahom

$P_k (t) = \prod_{i=-N_1 , i \neq k}^{N_2} \frac{t-t_i}{t_k - t_i}, \; k=-N_1 , -N_1 +1, \dots N_2 -1, N_2$

(6)

Stupeň polynómu P_k(t) je N-1, pretože N=N₂+N₁+1. Ak zvolíme N=4, tak dostaneme Lagrangeove polynómy 3. rádu. Tento konkrétny prípad aproximácie sa nazýva aj kubická Lagrangeova interpolácia. Hlavnou charakteristikou Lagrangeovej aproximácie je presná rekonštrukcia hodnôt vstupných vzoriek. Je to dôsledok vlastnosti Langrangeových polynómov danej nasledovným vzťahom

$P_k (t_n) = \left \{ \begin{array}{l} 1, k=n \\ 0, k \neq n \end{array} \right . ,-N_1 \leq n \leq N_2$

(8)

ktorú keď aplikujeme v rov.(6) dostaneme

$y_c(nT_x) = x[n] , \; -N_1 \leq n \leq N_2$

(9)

Na obr.3 je zobrazená Lagrangeova kubická interpolácia. Zvolené štyri vstupné vzorky {x[n_ℓ-1], x[n_ℓ], x[n_ℓ+1], x[n_ℓ+2]} získame vzorkovaním časovo spojitého signálu x_c(t) so vzorkovacou periódou T_x=10 ms. Vypočítame hodnotu vzorky y[ℓ] = y(t_ℓ), ktorá sa nachádza medzi vzorkami x(n_ℓT_x), a x(n_ℓT_x+1) v časovom okamžiku t_ℓ = n_ℓT_x +(2/3)T_x. Pomocou rov.(7) vypočítame štyri Lagrangeove polynómy tretieho rádu. V tomto prípade sme zvolili N₁=1 a N₂=2, preto sú kubické Lagrangeove polynómy vypočítané pre k = -1, 0, 1, 2 a sú označené ako P_-1(t), P₀(t), P₁(t) a P₂(t) a sú zobrazené na Obr.3. Nakoniec použijeme rov.(6) pre výpočet hodnôt požadovaných vzoriek y[ℓ] = y(t_ℓ).

Z Obr.3 môžeme vidieť výsledný interpolant, označený čiarkovanou čiarou zakončenou štvorčekom je veľmi dobrou aproximáciou pôvodného spojitého signálu x_c(t), pre časový okamžik t=t_ℓ. Ako bolo skôr uvedené, alternatívny prístup pre polynomiálnu interpoláciu je použitie B-splajnových funkcií. Pre splajnové funkcie sa v Matlabe používa funkcia spline.

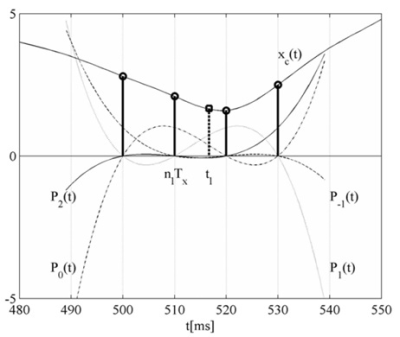
Obr. 3 Lagrangeova interpolácia s kubickými polynómami P_-1(t), P₀(t), P₁(t), P₂(t). Plné čiary zakončené prázdnym krúžkom predstavujú vstupné vzorky {x[n_ℓ-1], x[n_ℓ], x[n_ℓ+1], x[n_ℓ+2]} a čiarkovaná čiara s prázdnym štvorčekom na konci predstavuje výsledný interpolant y[ℓ]

Napríklad funkcia spline poskytuje interpoláciu s kubickou splajnovou funkciou. Príkaz:

yℓ = spline( t, x, tl );

vypočíta výstupné vzorky yℓ ako výsledok kubickej splajnovovej interpolácie pre vstupné premenné: t je vektor časových okamžikov vstupných vzoriek, x je vektor hodnôt vstupných vzoriek (má rovnakú dĺžku ako vektor t), tℓ je vektor časových okamžikov výstupných vzoriek.

3. Polynomiálna interpolácia založená na hybridnom analógovo – číslicovom modeli

Ako bolo predtým uvedené v kap.1, tak interpolácia môže byť považovaná v podstate za problém rekonštrukcie. Môžeme si predstaviť proces určenia interpolovaných hodnôt (interpolantu) ako postup dvoch krokov. V prvom kroku, aproximácia spojitého signálu y_c(t) je založená na rekonštrukcii vzoriek existujúcej vstupnej postupnosti {x[n]}. V druhom kroku je y_c(t) je vzorkovaný v požadovaných časových okamžikoch. Hybridný analógovo-číslicový model pre rekonštrukciu signálu a prevzorkovanie je zobrazený na obr.4.

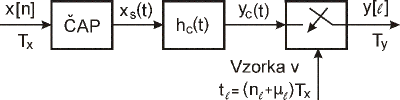
Obr. 4 Hybridný analógovo/číslicový model pre interpoláciu.

Spojitý signál y_c(t) je rekonštruovaný použitím číslicovo-analógového prevodníka (ČAP) a rekonštrukčného analógového filtra h_c(t). Výstupná vzorka y[ℓ] je získaná vzorkovaním y_c(t) v čase t_ℓ = n_ℓT_x+ μ_ℓT_x. Ako bude ďalej ukázane, tak veľmi efektívny interpolačný algoritmus môže byť získaný napodobnením hybridného modelu z obr.4. Uvažujme spracovanie signálu pomocou hybridného modelu na obr.4. Ideálny ČAP konvertuje postupnosť {x[n]} na postupnosť x_s(t) pozostávajúcu z váhovaných a posunutých spojitých impulzov

$x_s (t) = \sum_{n=- \infty}^{\infty} x[n] \delta (t-nT_x)$

(10)

Postupnosť x_s(t) je potom filtrovaná použitím analógového filtra s impulznou charakteristikou h_c(t) a výstupný spojitý signál y_c(t) sa získa pomocou konvolúcie

$y_s (t) = \sum_{n=- \infty}^{\infty} x[n] h_c (t-nT_x)$

(11)

Nakoniec, interpolant y[ℓ] je získaný vzorkovaním y_c(t) v časových okamžikoch t_ℓ. V praxi, sa použije len niekoľko vzoriek vstupného signálu na interpoláciu a h_c(t) je impulzná charakteristika fiktívneho analógového filtra s lineárnou fázou, ktorá je nulová mimo intervalu -NT_x/2 ≤ t ≤ (NT_x/2) -T_x. Z tohto dôvodu je hodnota y[ℓ] určená nasledovne

$y[\iota ] = y_c (t_{\iota}) = \sum_{k=-N/2}^{(N/2)-1} x[n_{\iota } -k] h_c ((k+ \mu_{\iota} )T_x)$

(12)

Predpokladá sa, že základný index n_ℓ vstupnej vzorky odpovedá centrálnej vzorke z intervalu -NT_x/2 ≤ t ≤ (NT_x/2) -T_x, kde interval dĺžky N je párne celé číslo. Interpolačný systém podľa Obr.4 môže byť implementovaný číslicovo napodobniac impulznú charakteristiku fiktívneho analógového filtra h_c(t) pomocou po častiach polynomiálnych funkcií premennej t. Presne povedané h_c(t) je tvorená z polynómov premennej t v každom intervale:{kT_x,(k+1)T_x} pre k = -N/2, -(N/2)+1, … ,(N/2)-1. Pre dosiahnutie polynomiálnej interpolácie vyjadríme impulznú charakteristiku h_c(t) v tvare

$h_c ((k+ \mu_{\iota} )T_x) = \sum_{m=0}^M c_m (k) \mu_{\iota }^m$

$pre \; k=-N/2,-(N/2)+1, \dots , (N/2)-1$

(13)

kde c₀(k), c₁(k), … ,c_M(k), sú koeficienty a M ≤ N-1 je stupeň polynómov. Interpolačné koeficienty môžeme vypočítať pomocou nasledujúceho jednoduchého vzťahu

$\sum_{m=0}^M c_m (k) x^m = \prod_{j=-(N/2)-1, j \neq k}^{N/2} \frac{j-x}{-k+j}$

$pre \; k=-N/2,-(N/2)+1, \dots , (N/2)-1$

(14)

V tab.1 sú tieto koeficienty uvedené pre kubické Lagrangeove polynómy a v tab.2 pre Lagrangeove polynómy 5. rádu. Použijeme ich neskôr aj pri prevzorkovaní diskrétneho signálu pomocou Farrowovho filtra. Ak sa spojitá premenná μ_ℓ mení od 0 po 1, tak rov.(12) nadobdne tvar

$h_c (t) = \sum_{m=0}^M c_m (k) \left ( \frac{t-kT_x}{T_x} \right )^m$

$pre \; k=-N/2,-(N/2)+1, \dots , (N/2)-1$

(15)

Polynomiálny interpolačný filter h_c(t) jeurčený výberom stupňa polynómov a hodnotami koeficientov c₀(k), c₁(k), … ,c_M(k). V mnohých aplikáciách je možné dosiahnuť uspokojivé výsledky pomocou Lagrangeových polynómov alebo B-splajnových funkcií.

Tab. 1 Lagrangeove koeficienty pre kubickú interpoláciu.

k	m=0	m=1	m=2	m=3
1	0	-1/6	0	1/6
0	0	1	1/2	-1/2
-1	1	-1/2	-1	1/2
-2	0	-1/3	1/2	-1/6

Tab. 2 Lagrangeove koeficienty pre interpoláciu 5. rádu.

k	m=0	m=1	m=2	m=3	m=4	m=5
-2	0	0.05	-4.1667e-02	-4.1667e-02	4.1667e-02	-8.3333e-02
-1	0	-0.5	0.6667	8.3333e-02	-0.203	4.1667e-02
0	1	-0.3333	-1.25	4.1667e-02	0.25	-8.3333e-02
1	0	1	0.6667	-0.5833	-0.1667	8.3333e-02
2	0	-0.25	-4.1667e-02	0.2917	4.1667e-02	-4.1667e-02
3	0	3.3333e-02	0	-4.1667e-02	0	8.3333e-02

4. Implementácia polynomiálnych interpolačných filtrov používajúca Farrowovu štruktúru

Aproximácia analógového filtra s impulznou charakteristikou h_c(t) na polynomiálnom základe umožňuje číslicovú implementáciu analógovo-číslicového modelu z obr.4. Dosadením h_c((k+μ_ℓ)T_x) z rov.(13) do rov.(12) dostaneme nasledovný výraz pre výpočet interpolantu y[ℓ]

$y [\iota] = x[n_{\iota } -k] \sum_{m=0}^{M} c_m(k) \mu_{\iota}^m$

(16)

ktorý je možné upraviť do tvaru

$y [\iota] = \sum_{m=0}^{M} \mu_{\iota}^m \left ( \sum_{k=-N/2}^{(N/2)-1} c_m(k) x[n_{\iota } -k] \right )$

(17)

Pre zjednodušenie výpočtu môžeme tento výraz napísať v tvare

$y [\iota] = \sum_{m=0}^{M} v_m [n_{\iota }] \mu_{\iota }^m$

(18)

kde v_m[n_ℓ] je výsledkom konvolúcie

$v_m [n_{\iota }] = \sum_{k=-N/2}^{(N/2)-1} c_m[k] x[n_{\iota } -k]$

(19)

Rovnica (19) prezentuje vstupno-výstupný vzťah filtra s konečnou impulznou odozvou (KIO), ktorého koeficienty impulznej odozvy sú c_m(-(N/2), c₁(-(N/2)+1), … ,c_m((N/2)-1). Je zrejme, že prenosová funkcia tohto KIO filtra C_m(z) je daná vzťahom

$C_m (z) = \sum_{k=0}^{N-1} c_m(k) z^{-k}, \; m=0,1, \dots ,M$

(20)

Koeficienty c_m(k) sú pre daný návrh konštanty, ktoré sú nezávislé od μ_ℓ a sú určené iba filtrom s impulznou odozvou h_c(t). Rovnica (18) je sama o sebe polynomiálna a závisí na μ_ℓ, čo je jediný premenný parameter v štruktúre. Koeficienty môžeme vypočítať pomocou rov.(14) a sú konštantné pre daný rád filtra. Zodpovedajúca štruktúra, ktorá implementuje rov.(18) a (19) je Farrowova štruktúra pozostávajúca z M +1 KIO subfiltrov s konštantnými koeficientmi, zapojených paralelne, ktorých výstupy sú vynásobené mocninami parametra μ_ℓ, a následne sa spolu sčítajú ako to vidno na obr.5. Na obr.6 je sú zobrazené detaily KIO subfiltra z Farrowovej štruktúry na obr.5.

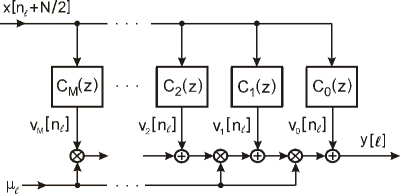
Obr.5 Bloková schéma Farrowovej štruktúry pre interpoláciu.

Možno si všimnúť, že bloková schéma na obr.5 implementuje kauzálny Farrowov filter. V tejto kapitole sme sa zamerali na problém výpočtu hodnoty vzorky jediného interpolantu, ktorý sa nachádzala medzi dvoma známymi vzorkami. Ako bolo ukázané, tak pozícia novej interpolovanej vzorky môže byť ľubovoľné zvolená v časovom intervale medzi dvomi po sebe idúcimi vzorkami. Jediným nastaviteľným parametrom je zlomkový parameter μ_ℓ. Môžeme adaptovať zmeny μ_ℓ, aby sme konvertovali vstupnú vzorkovaciu frekvenciu f_x na požadovanú výstupnú vzorkovaciu frekvenciu f_y. Vo všeobecnosti tento prístup je použiteľný, keď pomer f_x/f_y je racionálne, alebo iracionálne číslo a je vhodný pre zvýšenie ako aj zníženie vzorkovacej frekvencie.

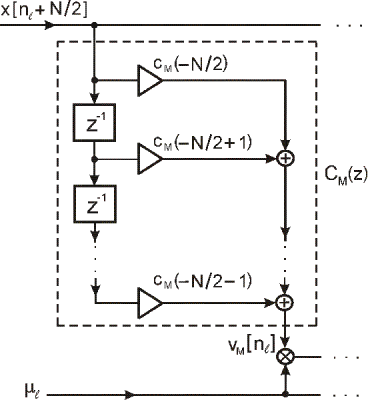
Obr. 6 Detaily KIO subfiltra s dĺžkou N.

Použitím metódy založenej na polynómoch a Farrowovej štruktúry môžeme účinne realizovať zmenu vzorkovacej frekvencie s ľubovoľným faktorom [8].

5. Experimentálne výsledky

Experimentprevzorkovania sme vykonali pre diskrétny signál získaný vzorkovaním spojitého signálu s komplexným frekvenčným spektrom

$\overline{X} (\omega) = \pi e^{- | \omega |}$

(21)

ohraničeným maximálnou kruhovou frekvenciou ω_m =10 [rad.s^-1]. Ohraničenému spektru odpovedá v časovej oblasti spojitý signál

$x(t) = \frac{1}{1+t^2} (1-e^{- \omega_n } cos \omega_m t + te^{- \omega_n } sin \omega_m t), \; t \in <-\infty , \infty>$

(22)

Jeho grafické zobrazenie na časovom intervale $t \in <-15,15>$ je na obr.7.

Obr.7 Spojitý signál x(t).

Kruhovú vzorkovaciu frekvenciu pre tento signál volíme ω_x = 30 [rad.s^-1]. Vstupný diskrény signál x(nT_x) dostaneme vzorkovaním spojitého signálu x(t) daného rov.(22) so vzorkovacou periódou T_x=2π/ω_x = 0.2094395102 [s], resp. vzorkovacou frekvenciou f_x = 4.774648293[Hz]. Vykonali sme prevzorkovanie signálu x(nT_x) interpolačnými metódami pomocou: a) kubického splajnu definovaného v Matlabe funkciou spline (x,Y,xx), b) Farrowového filtra, c) Lagrangeových polynómov 3.rádu. Koeficienty pre Farrowov filter sme zvolili pre dĺžku N=4 a 5 (3. a 5. rádu). Vypočítali sme strednú kvadratickú chybu

$\epsilon = \frac{1}{M} \sum_{n=0}^M (x(nT_y) - \hat{x}(nT_y))^2$

(23)

kde $\hat{x}(nT_y)$ je prevzorkovaný signál, x(nT_y) diskrétny signál získaný vzorkovaním pôvodného spojitého signálu s novou vzorkovacou periódou T_y a počtom vzoriek L. Vypočítané hodnoty strednej kvadratickej chyby ε pre zvyšovanie vzorkovacej frekvencie sú uvedené v tab.3 a pre znižovanie vzorkovacej frekvencie v tab.4

Tab. 3 Vypočítané hodnoty strednej kvadratickej chyby – zvyšovanie vzorkovacej frekvencie

f_y	T_y	L	Kubický splajn	Farrowov filter N=4	Farrowov filter N=6	Lagrangeové polynómy
5.1	0,19607843137254	154	6.2709e-11	1.1282e-03	1.4795e-02	9.6483e-06
7.9	0,12658227848101	238	1.5299e-10	1.1306e03	9.9121e-03	6.2461e-06
10.4	0.09615384615384	313	1.5786e-10	1.1320e-03	7.8587e-03	4.8165e-06
21.5	0.04651162790697	646	1.5789e-10	1.1335e-03	4.4295e-03	2.3978e-06
33.7	0.02967359050445	1012	1.5808e-10	1.1341e-03	1.3621e-03	1.0485e-06
44.5	0.02212389380531	1357	1.5812e-10	1.1345e-03	1.2714e-03	7.9448e-07
50.08	0.01996805111821	1503	1.5817e-10	1.1348e-03	1.2825e-03	7.3128e-07
60	0.01666666666666	1801	1.5814e-10	1.1346e-03	1.2655e-03	1.4169e-07

Tab. 4 Vypočítané hodnoty strednej kvadratickej chyby – znižovanie vzorkovacej frekvencie

f_y	T_y	L	Kubický splajn	Farrowov filter N=4	Farrowov filter N=6	Lagrangeové polynómy
4.7	0.212765957446809	142	2.4095e-11	1.1289e-03	1.0895e-03	2.1638e-09
4.35	0.229885057471264	131	2.5248e-10	1.1338e-03	1.1836e-03	1.0676e-08
4.1	0.243902439024390	124	7.5161e-11	1.1271e-03	1.0556e-03	4.8397e-09
3.5	0.285714285714286	106	7.0842e-11	1.1254e-03	1.2190e-03	4.1498e-09
3.2	0.312500000000000	97	3.0871e-10	1.1249e-03	1.1027e-03	1.2138e-08
2.5	0.400000000000000	76	1.2213e-10	1.1229e-03	8.5381e-04	9.0194e-09
1.2	0.833333333333333	37	9.4382e-10	2.2119e-03	2.3935e-03	4.3116e-08
0.7	1.428571428571429	22	2.6233e-11	3.6427e-03	4.0164e-03	1.4169e-07

Pre ilustráciu je na obr.8 zobrazený pôvodný, avšak harmonický diskrétny signál so vzorkovacou frekvenciou f_x = 302.7 [Hz] a prevzorkovaný signál vypočítaný pomocou príkazu spline v Matlabe pre zvýšenú vzorkovaciu frekvenciu f_y = 501.3 [Hz]. Pre tento prípad je stredná kvadratická chyba ε =3.0980.10^-9 a počet vzoriek po prevzorkovaní L=301.

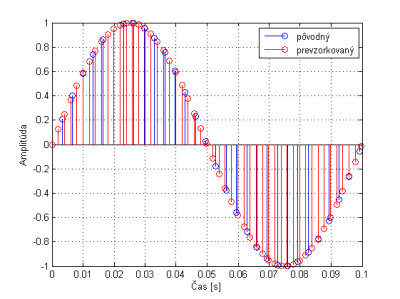
Obr.8 Pôvodný a prevzorkovaný signál zobrazený na intervale $t \in <0,0.1>$ .

6. Záver

V tomto článku sme navrhli spôsob zmeny vzorkovacej frekvencie diskrétneho signálu s ľubovoľným faktorom pomocou techniky známej ako interpolácia. Vypracovali sme programové prostriedky pre prevzorkovanie s využitím Lagrangeových polynómov, Farrowovej štruktúry a kubického splajnu v prostredí Matlab. Vypočítané hodnoty strednej kvadratickej chyby pre zvyšovanie a znižovanie vzorkovacej frekvencie sú uvedené v tabuľkách. Z uvedených výsledkov je vidieť, že najlepšie výsledky z hľadiska strednej kvadratickej chyby dáva interpolácia s kubickým splajnom, za ňou ďalej nasleduje interpolácia s Lagrangeovými polynómami a nakoniec metóda používajúca Farrowovu štruktúru, avšak je potrebné vziať do úvahy, že táto používa subfiltre veľmi nízkeho rádu.

Literatúra

Crochiere, R. E., Rabiner, L. R.: Multirate Digital Signal Processing, Englewood Cliffs, NJ: Prentic- Hall, 1983, ISBN 0-13-605162-6.
Jonvanović-Doleček, G.: Multirate Systems: Design & Applications. London , U. K. :Idea Group Publshing, 2002, ISBN 1-59140-019-8.
Malvar, H. S.: A Link between Transform Coding and Multirate Filter Banks. IEEE Int. Symp. Circuit and Systems, 1988, pp. 835-838.
Campbel, W. M., Parks, T.W.: Design of a Class of Multirate Systems. In: ICASSP Proceedings, 1995, pp. 1308-1311.
Harris, F.J .: Multirate Signal Processing for Communications. Upper Saddle River, NJ: Prentice – Hall, 2004
Fliege, N. J.: Multirate Digital Signal Processing: Multirate Systems, Filter Banks, Wavelets. John Willy & Sons, Chichester, 1994 ISBN 0-471-93976-5.
Zavacký, J., Mihalík, J.: Diskrétne spracovanie signálov, LČSOV FEI TU Košice, 2011, ISBN 978-80-553-0730-5, (319 strán).
Milić, J.: Multirate Filtering for Digital Signal Processing: Matlab Applications, Hershey, New York, 2009, ISBN 978-1-60566-178-0.

Spoluautorom článku je Ing. Jozef Zavacký, PhD., Katedra elektroniky a multimediálnych telekomunikácií, Fakulta elektrotechniky a informatiky, Technická univerzita v Košiciach, Slovenská republika

O časopise

Meta

RSS

Zmena vzorkovacej frekvencie s ľubovoľným faktorm

Napísať príspevok

Rubriky

Burza práce

Štúdijné materiály

Archív