Krátkodobá Fourierova transformácia

08. December, 2014, Autor článku: Zavacký Jozef, MATLAB/Comsol
Ročník 7, číslo 12 Pridať príspevok

p17657_icon Článok sa venuje krátkodobej Fourierovej transformácii. Táto transformácia je častým nástrojom časovo frekvenčnej analýzy nestacionárnych signálov. Princíp je veľmi jednoduchý. Vynásobíme signál f(t), ktorý má byť analyzovaný s určitým typom symetrickej oknovej funkcie (oknom) konštantnej dĺžky a potom vypočítame Fourierovu transformáciu jednotlivých úsekov signálu f(t). Spektrum krátkodobej Fourierovej transformácie je vo všeobecnom prípade komplexná funkcia dvoch reálnych premenných, času a frekvencie. Pre jeho grafické znázornenie sa používa tzv. spektrogram.

1. Úvod

Fourierova transformácia (FT) rozkladá spojitý signál na jednotlivé frekvenčné zložky. Neposkytuje však informáciu v ktorých časových okamžikoch, aké frekvenčné zložky spektra sa vyskytujú, t.j. časová informácia sa stráca. Je to dôsledkom toho, že bázové funkcie pri Fourierovej transformácii rovnomerne prekrývajú celú časovú os. Pre určenie časovej lokalizácie frekvenčných zložiek je nutné využiť iné transformačné postupy a iné výpočtové metódy. Jedným z možných postupov ako analyzovať časový výskyt frekvenčných zložiek nestacionárnych signálov, je použitie časovo-frekvenčných postupov (transformácií). Tieto môžu byť rozdelené do dvoch základných tried podľa výpočtového postupu:

lineárne (zarňajúce predovšetkým krátkodobú Fourierovu transformáciu a waveletovú transformáciu)
nelineárne (zarňajúce predovšetkým kvadratické Cohenove, afinné a hyperbolické transformácie)

2. Krátkodobá Fourierová transformácia

Častým nástrojom časovo frekvenčnej analýzy nestacionárnych signálov je krátkodobá Fourierova transformácia – KDFT (angl. Short Time Fourier Transform, STFT) . Princíp je nasledovný. Vynásobíme signál f(t), ktorý má byť analyzovaný s určitým typom symetrickej oknovej funkcie (oknom) w*(t-τ) konštantnej dĺžky a potom vypočítame Fourierovu transformáciu jednotlivých úsekov signálu f(t). KDFT spojitého signálu f(t) je definovaná takto:

$KDFT\{x(t)\}(\tau , \omega) \equiv X(\tau , \omega) =$

$= \int_{-\infty}^{\infty} f(t)w^*(t-\tau )e^{j \omega t}dt = <f(t), w^*(t-\tau )e^{j \omega t}>$

(1)

kde symbol (*) vyjadruje komplexnú konjugáciu a τ – časové posunutie okna. Najpoužívanejšími oknovými funkciami sú pravouhlé, Hammingove, Kaiserove alebo Hannove okno. Ak oknová funkcia je Gaussova funkcia tak KDFT sa nazýva Gáborova transformácia [1]. Pri výpočte KDFT možno na časovom intervale danom dĺžkou okna považovať nestacionárny signál za približne stacionárny. Presnosť a vhodnosť KDFT závisí na voľbe časovej oknovej funkcie, jej veľkosti a na prípadnom prekrytí jednotlivých segmentov. Prekrytie zabezpečuje, že nedôjde k skokovým zmenám frekvencií.

KDFT poskytuje kompromis medzi časovou a frekvenčnou reprezentáciou signálov. V tomto prípade nemožno dosiahnúť súčasne vysokého rozlíšenia v čase a frekvencii. Voľba dlhého okna umožňuje dobré frekvenčné rozlíšenie (Δ_ω), ale horšie časové rozlíšenie (Δ_t) a naopak. Preto vždy musíme dospieť ku kompromisu medzi presnosťou určenia frekvencie a času, teda nájsť optimálnu šírku okna. Tá je po celú dobu výpočtu konštantná, čo je hlavný rozdiel medzi KDFT a waveletovou transformáciou. Aby sme mohli opísať časovo-frekvenčné rozlíšenie KDFT uvažujme časovo-frekvenčné okno odpovedajúce příslušnej oknovej fukcii w*(t). Jeho stred je v bode S_tω(t₀,ω₀) a velkosti strán sú 2Δ_t a 2 Δ_ω. Príslušné parametre sa vypočítajú v časovej oblasti takto [2],[3]

$t_0=\int_{-\infty}^{\infty} t . \frac{|w(t)|^2}{\|w\|^2} dt$

(2)

$\Delta_t= \left ( \int_{-\infty}^{\infty} (t-t_0)^2 . \frac{|w(t)|^2}{\|w\|^2} dt \right )^{1/2}$

(3)

Vo frekvenčnej oblasti analogicky môžeme písať

$\omega_0=\int_{-\infty}^{\infty} \omega . \frac{|W(\omega)|^2}{\|W\|^2} d\omega$

(4)

$\Delta_{\omega}= \left ( \int_{-\infty}^{\infty} (\omega - \omega_0)^2 . \frac{|W(\omega)|^2}{\|W\|^2} d \omega \right )^{1/2}$

(5)

pričom W(ω) je Fourierova transformácia okna w*(t). Treba si uvedomiť, že stred t₀ a parameter Δ_t okna w*(t) sú definované analogicky ako stredná hodnota a smerodajná odchylka náhodnej premennej, podobne je tomu aj pre ω₀ a Δ_ω. KDFT poskytuje informáciu o signáli f(t) a jeho spektre F(ω) v časovo-frekvenčnom okne

$[\tau + t_0 - \Delta_t, \tau + t_0 + \Delta_t] \times [\omega + \omega_0 - \Delta_{\omega}, \omega + \omega_0 + \Delta_{\omega}]$

(6)

Poloha časovo-frekvenčného okna je určená pomocou parametrov τ a ω. Tvar časovo-frekvenčného okna je nezávislý od τ a ω, preto dostávame rovnaké rozlíšenie v časovo-frekvenčnej rovine ako to ukazuje Obr. 1.

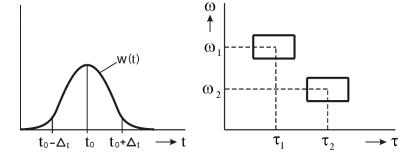
Obr. vľavo – 1. Časové okno w(t), vpravo – časovo-frekvenčné okná určené pomocou parametrov τ a ω v časovo-frekvenčnej rovine.

Medzi Δ_t a Δ_ω platí nasledujúci vzťtah

$\Delta_t \Delta_{\omega} \geq \frac{1}{2}$

(7)

Tento vzťah je známy ako Heisenbergov princíp neurčitosti, pričom rovnosť platí ak w(t) je Gaussova funkcia v tvare

$w(t) = \sqrt{\alpha / \pi e^{-\alpha t^2}} , \alpha > 0$

(8)

Pre všetky ostatné oknové funkcie platí nerovnosť. Z princípu neurčitosti vyplýva, že signály sa nedajú s ľubovoľnou presnosťou lokalizovať naraz vo frekvencii aj v čase, resp. nie je možné presne vedieť aká frekvencia sa vyskytuje v danom časovom okamžiku. Plocha časovo- frekvenčného okna je vždy minimálne 2. Aby sme boli schopní v transformačnej oblasti reprezentovať ľubovoľný signál f(t) musia bázové funkcie pokrývať celú časovo-frekvenčné rovinu, t. j. rovinu si svojimi časovo-frekvenčnými oknami musia medzi seba rozdeliť. Delenia časovo-frekvenčnej roviny pre STFT je znázornené na Obr. 2.

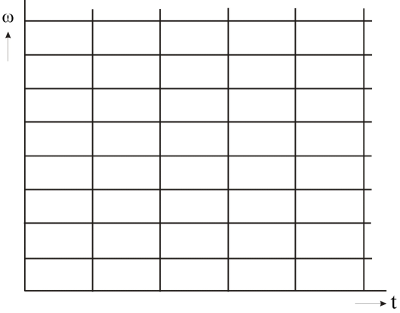
Obr. 2. Delenie časovo frekvenčnej roviny pre KDFT.

Spektrum KDFT je vo všeobecnom prípade komplexná funkcia dvoch reálnych premenných. Pre jeho grafické znázornenie sa používa tzv. spektrogram, čo je kvadrát absolútnej hodnoty spektra KDFT [4],[5]

$SPEC(t,\omega) = |KDFT(t,\omega)|^2$

(9)

Doteraz uvedená teória sa týkala spojitých signálov a spektrum KDFT bolo tiež spojité. V praxi číslicového spracovania signálov je ovšem signál diskrétny v čase. Preto v definícii KDFT rov. (1) nahradíme spojitú FT Fourierovou transformáciou diskrétnych signálov (FTD) [6] označovanú často tiež ako DTFT(z angl. Discrete Time Fourier Transform). Tak dostaneme rovnicu

$F(e^{j \tilde{m}},m) = \sum_{n=-\infty}^{\infty} f(n)w(n-mN) e^{-jn \tilde{m}}$

(10)

kde normovaná kruhová frekvencia

$\tilde{\omega} = \omega T_d = \frac{2 \pi f}{f_d}$

(11)

pričom T_d=1/f_d je diskretizačná perióda. Spektrum podľa rov. (10) je spojitou periodickou funkciou normovanej kruhovej frekvencie $\tilde{\omega}$ s periódou 2π. Avšak v praxi pracujeme iba s diskrétními frekvenciami

$\tilde{\omega} = 2 \pi k / M, \; k=1,2, \dots , M-1$

(12)

A spektrum KDFT pre diskrétny čas a diskrétne frekvencie je dané

$F(k,m) = \sum_{n=0}^{N-1} f(n) w(n-mN) e^{j2 \pi nk/M}$

(13)

Funkcia F(k,m) je periodická v k s periódou M.

3. Experimenty

Ako prvý sme pre časovo frekvenčnú analýzu použili harmonický signál s lineárne rastúcou frekvenciou od 0 do 300 Hz na časovom intervale od 0 do dvoch sekúnd. Na Obr. 3 je tento signál zobrazený kvôli dobrej rozlíšiteľnosti v čase len na intervale od 0 do 0,5 s. Vzorkovacia frekvencia je zvolená 1 kHz.

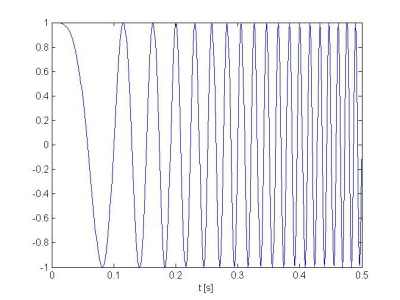
Obr. 3. Harmonický signál s lineárne rastúcou frekvenciou od 0 do 300 Hz.

Pre generovanie signálu na Obr. 3 bol použitý Matlabovský príkaz chirp. Pre výpočet spektrogramu je aplikované Hammingove okno dĺžky N=256 s prekrytím 250 vzoriek medzi po sebe nasledujúcimi oknami. Pre výpočet spektra je použitá 256 bodová FFT. Program v Matlabe pre výpočet a zobrazenie spektrogramu (Obr.4) bude

clc; t = 0:0.001:2; x = chirp(t,0,2,300); [S,F,T,P] = spectrogram(x,hamming(256),250,256,1E3); surf(T,F,10*log10(P),'edgecolor','none'); axis tight; view(0,90); xlabel('Čas [s]'); ylabel('Frekvencia [Hz]'); colorbar

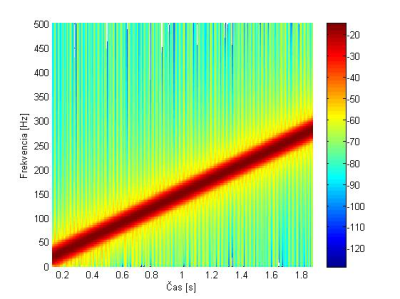
Obr. 4. Spektrogram signálu chirp s Hammingovým oknom s dĺžkou N=256.

Trojrozmerné zobrazenie (3R) spektrogramu z Obr. 4 v decibelovom vyjadrení je na Obr. 5

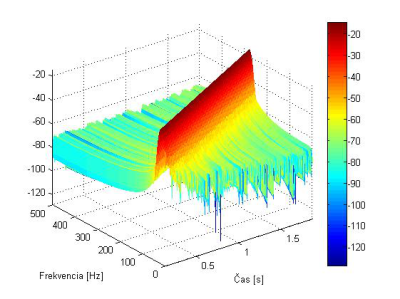
Obr. 5. 3R Spektrogram signálu chirp s Hammingovým oknom s dĺžkou N=256.

a v nedecibelovom vyjadrení na Obr. 6.

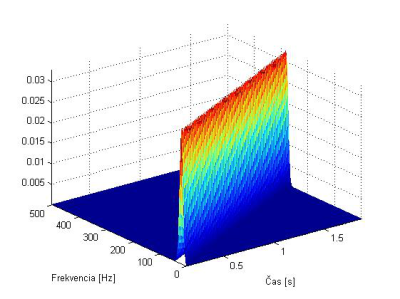
Obr. 6. 3R Spektrogram signálu chirp s Hammingovým oknom s dĺžkou N=256 v nedecibelovom vyjadrení.

Ďalšie signály x₁(t), x₂(t), ktorých spektrogramy vypočítame dostaneme frekvenčnou moduláciou harmonického sínusového signálu, pričom modulačné signály majú časový priebeh ako to vidno na Obr. 7a a Obr. 7b. Minimálna frekvencia signálov x₁(t), x₂(t) je 1 kHz a maximálna 4 kHz.

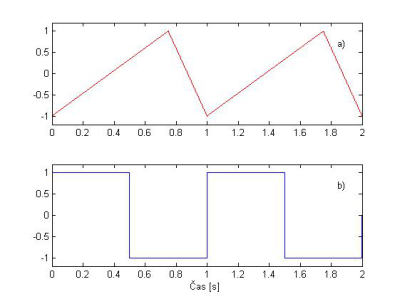
Obr. 7. Modulačný signál a) trojuholníkový c₁(t), b) pravouhlý c₂(t).

Pre generovanie x₁(t), x₂(t), použijeme zápis v Matlabe pomocou príkazov

t = 0:1/fs:2; x1 = vco(sawtooth(2*pi*t,0.75),[0.1 0.4]*fs,fs); x2 = vco(square(2*pi*t),[0.1 0.4]*fs,fs);

kde fs je vzorkovacia frekvencia 10kHz. Spektrogramy pre uvedené signály x₁(t), x₂(t) sú na Obr. 8 pre Hammingové okno a na Obr. 9 pre Kaiserove okno s parametrom β=20. Pre výpočet spektier je použitá 256 bodová FFT.

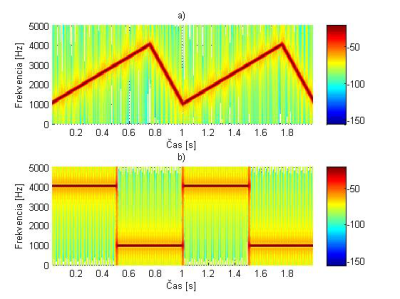
Obr. 8. Spektrogramy signálov pre a) x₁(t), b) x₂(t) pre Hammingove okno s dĺžkou N=256, s prekrytím 220 vzoriek.

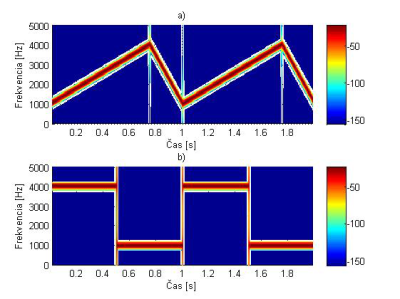
Obr. 9. Spektrogramy signálov pre a) x₁(t) , b) x₂(t) – pre Kaiserove okno s dĺžkou N=256, β=20, s prekrytím 220 vzoriek.

Trojrozmerné zobrazenia spektrogramov z Obr. 8 a 9 sú na Obr. 10 až 13.

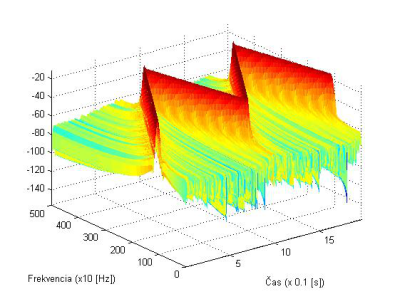
Obr. 10. Spektrogram signálu x₁(t) s Hammingovým oknom s dĺžkou N=256, s prekrytím 220 vzoriek.

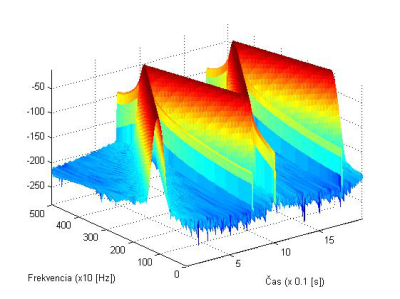
Obr. 11. Spektrogram signálu x₁(t) s Kaiserovým oknom s dĺžkou N=256, β=20, s prekrytím 220 vzoriek.

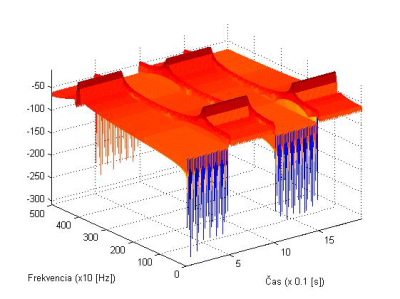
Obr. 12. Spektrogram signálu x₂(t) s Hammingovým oknom s dĺžkou N=256, s prekrytím 220 vzoriek.

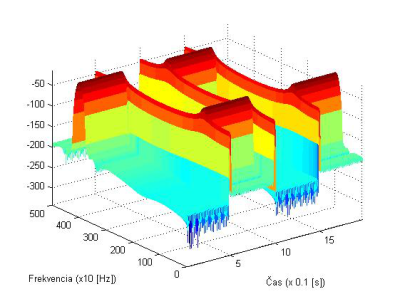
Obr. 13. Spektrogram signálu x₂(t) s Kaiserovým oknom s dĺžkou N=256, β=20, s prekrytím 220 vzoriek.

Ďalej budú ukázané spektrogramy signálov x₁(t), x₂(t) pre Hammingove a Kaiserove okno s parametrom β=20, ale s kratšou dĺžkou N=64. Prekrytie je 60 vzoriek, pre výpočet spektra je použitá 64 bodová FFT, fs=10kHz. Odpovedajúce spektrogramy sú na Obr. 14 pre Hammingové okno a na Obr. 15 pre Kaiserove okno. Výsledky s kratším oknom s dĺžkou 64, ukazujú stratu vo frekvenčnom rozlíšení a dobré časové rozlíšenie, v porovnaní so spektrogramami na Obr. 8 a 9. Prejavil sa blokový efekt v spektrogramoch pre signál x₁(t).

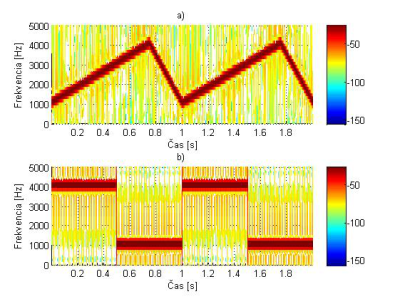
Obr. 14. Spektrogramy signálov x₁(t) a x₂(t) s Hammingovým oknom s dĺžkou N=64.

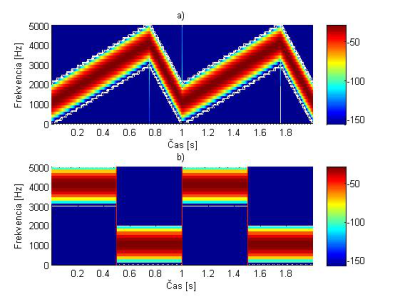
Obr. 15. Spektrogramy signálov x₁(t) a x₂(t) s Kaiserovým oknom s dĺžkou N=64.

pretože je použitá iba 64 bodová FFT. V tomto prípade by bolo užitočnejšie použiť 256 bodovú FFT.

4. Záver

Po teoretickej analýze KDFT boli vypočítané a zobrazené spektrogramy pre tri signály s časom sa meniacou frekvenciou. Pre výpočet spektrogramov boli použité Hammingove a Kaiserove okno s parametrom β=20 s dĺžkou N=256, s prekrytím 250 vzoriek ako aj s kratšou dĺžkou N=64 a prekrytím 60 vzoriek. Výsledky s kratším oknom s dĺžkou 64, ukazujú stratu vo frekvenčnom rozlíšení a prejavil sa blokový efekt v spektrogramoch.

Literatúra

D. Gabor, “Theory of Communication”, Journal of the IEE, Vol. 93, 1946, p. 429-457.
S. Mertins, “Signal Analyssis, Wavelets, Filter banks, Time frequency Transforms and Applications”, John Wiley and Sons, ISBN 0-470-84138-4, 1999.
L. Cohen, “Time-Frequency Analysi”, Prentice Hall, New Jersey, 1995, ISBN 0-13-594532-1.
J.B. Allen, L.R. Rabinar, “A Unified Approach to Short-Time Fourier Analysis and Synthesis”, Proc. IEEE, Vol. 65, 1997, p. 1558-1564.
M.R. Portnoff, “Time-Frequency Representation of Digital Signals and Systems Based on Short Time Fourier Analysis”, IEEE Trans. ASSP, Vol. 28, 1980, p. 55- 69.
J. Mihalík, J. Zavacký, “Diskrétne spracovanie signálov” ,LČSOV FEI TU Košice, 2011, ISBN 978-80-553-0730-5.

O časopise

Meta

RSS

Krátkodobá Fourierova transformácia

Napísať príspevok

Rubriky

Burza práce

Štúdijné materiály

Archív