Diskrétna multiwaveletová transformácia a jej implementácia s DGHM multiwaveletmi

02. Marec, 2015, Autor článku: Zavacký Jozef, Elektrotechnika
Ročník 8, číslo 3 Pridať príspevok

p17764_icon Článok sa zaoberá teoretickou analýzou a implementáciou diskrétnej multiwaveletovej transformácie (DMWT) jednorozmerných diskrétnych signálov. Navrhnutý je spôsob implementácie jednorozmernej DMWT pre DGHM (Donovan, Geronimo, Harding, Massopust) multiwavelety s využitím diskrétnej konvolúcie a skalárnych filtrov, z ktorých pozostávajú multifiltre (vektorové filtre). Skreslenie na hraniciach spracovávaných signálov je eliminované ich vhodným symetrickým predĺžením v procese implementácie RDMWT.

1. Úvod

Waveletová transformácia sa v poslednej dekáde stala populárnou nielen v oblasti kompresie obrazu, ale aj pri odstraňovaní šumu, v počítačovej grafike, pri watermarkingu obrazu, pri detekcii hrán v obrazoch, v rôznych iných technických odboroch pri analýze fyzikálnych dejov a pod. [1-4]. Multiwavelety poskytujú lepšie vlastnosti a výsledky v aplikáciách spracovania obrazu v porovnaní so skalárnymi waveletami. Možno ich považovať za zovšeobecnenie skalárnych waveletov. Všeobecne DMWT môže mať r mierkových a r waveletových funkcií, vtedy hovoríme, že má násobnosť (multiplicitu) r. Väčšina DMWT používa dve mierkové a dve waveletove funkcie, pričom r môže mať teoreticky ľubovoľnú hodnotu [5]. Multiwaveletový rozklad môže byť realizovaný bankami filtrov, pričom rozkladové koeficienty v tomto prípade sú matice namiesto skalárov. Také vlastnosti ako je ortogonalita, symetria (t.j. lineárna fázová frekvenčná chrakteristika), vysoký rád aproximácie a krátky nosič (suport), resp. časový interval na ktorom (multiwavelety) trvajú sú základom pre ich úspešné aplikovanie pri spracovaní signálov. Súčasné splnenie uvedených vlastností nie je možné dosiahnúť pre skalárne wavelety. Dobre známymi multivaweletami sú DGHM, CL(0,2) a CL(0,3) (Chui a kol.) multiwavelety [6-7]

2. Teoretická analýza DMWT

Podobne ako v prípade skalárnej diskrétnej waveletovej transformácie, teória diskrétnej multiwaveletovej transformácie je založená na príncípe analýzy signálov s mnohonásobným rozlíšením. Mierkové a waveletové funkcie môžu byť zapísané ako stĺpcové vektory, t.j. multimierková funkcia $\varphi(t) = [\varphi_1 (t), \varphi_2 (t), \dots , \varphi_l (t), \dots , \varphi_r (t)]^T$ a rovnakým spôsobom môžeme definovať multiwaveletovu funkciu $\psi(t) = [\psi_1 (t), \psi_2 (t), \dots , \psi_l (t), \dots , \psi_r (t)]^T$ , kde T znamená transpozíciu. Analogicky ako skalárna mierková a waveletová funkcia aj multimierková $\varphi(t)$ a multiwaveletová $\psi(t)$ funkcia musia vyhovovať nasledujúcim maticovým (dilatačným) rovniciam [8]

$\varphi (t) = 2 \sum_{k} \tilde{g}_0 (k) \varphi (2t-k)$

(1)

$\psi (t) = 2 \sum_{k} \tilde{g}_1 (k) \varphi (2t-k) \; k \in Z$

(2)

kde namiesto skalárnych rozkladových koeficientov sú $\tilde{g}_0 (k)$ a $\tilde{g}_1 (k)$ rozkladové matice rozmeru $r \times r$ . Potom dvojica týchto matíc $\tilde{g}_0 (k), \tilde{g}_1 (k)$ , popisuje multiwaveletovú banku filtrov, pričom $g_0 (k) = \sqrt{2} \tilde{g}_0 (-k)$ je impulzná charakteristika vektorového dolnopriepustného (DP) filtra a $g_1 (k) = \sqrt{2} \tilde{g}_1 (-k)$ vektorového hornopriepustného (HP) filtra. Potom ich komplexné frekvenčné charakteristiky sú matice

$G_0 (e^{j \omega}) = \sum_{k} g_0 (k) e^{-j \omega k}$ a $G_1 (e^{j \omega}) = \sum_{k} g_1 (k) e^{-j \omega k}$

(3)

pričom ich prvky sú trigonometrické polynómy. O multiwaveletovej banke filtrov (MWBF), s konečnou impulznou odozvou (KIO) hovoríme vtedy, ak existuje take celé číslo N, že g₀(k)=0 a g₁(k)=0 pre k>N. MWBF je ortogonálna vtedy, keď vyhovuje maticovým rovniciam

$G_0 (e^{j \omega}) G_0^T (e^{-j \omega}) + G_0 (e^{j (\omega + \pi)}) G_0^T (e^{-j (\omega + \pi)}) = I_r$

$G_1 (e^{j \omega}) G_1^T (e^{-j \omega}) + G_1 (e^{j (\omega + \pi)}) G_1^T (e^{-j (\omega + \pi)}) = I_r$

$G_0 (e^{j \omega}) G_1^T (e^{-j \omega}) + G_0 (e^{j (\omega + \pi)}) G_1^T (e^{-j (\omega + \pi)}) = 0_r$

(4)

kde I_r je jednotková matica a 0_r nulová matica rozmeru $r \times r$ . Pre každý subpriestor $V_j \subset V_{j+1}$ opäť ako v skalárnom prípade je definovaný ortogonálny doplnok W_j rovnakým spôsobom, t.j.

$V_{j+1} = V_j \oplus W_j, \; j \in Z$

(5)

Potom $\{ 2^{j/2} \varphi_l (2^j t-k) \}$ a $\{ 2^{j/2} \psi_l (2^j t-k) \}$ , $k \in Z$ , $1 \leq l \leq r$ sú ortonormálne bázy subpriestoru V_j a komplementárneho subpriestoru W_j. Každý spojitý signál $f(t) \in V_0$ môže byť vyjadrený nasledovne

$f(t) = \sum_k \sum_{l=1}^r c_{0,l} (k) \varphi_l (t-k)$

(6)

z čoho vyplýva, že je úplne určený vektorovou postupnosťou {[c_0,1(k),…,c_0,r(k)]^T}. Pre J – záporné celé číslo, ktorému zodpovedá rozklad

$V_0 = V_{-1} \oplus W_{-1} = \dots = W_{-1} \oplus \dots \oplus W_{j} \oplus V_{j}$

(7)

Mierkové koeficienty DMWT vypočítame nasledovne

$c_j(k) = \sqrt{2} \sum_n \tilde{g}_0 (n-2k) c_{j+1}(n)$

(8)

a detailové koeficienty

$d_j(k) = \sqrt{2} \sum_n \tilde{g}_1 (n-2k) c_{j+1}(n)$

(9)

Rov.(8) a (9) predstavujú jednu úroveň výpočtu priamej DMWT. Jedna úroveň spätnej DMWT sa vypočíta takto

$c_{j+1}(n) = \sqrt{2} \sum_k \tilde{g}_0^T (n-2k) c_{j}(k) + \sqrt{2} \sum_k \tilde{g}_1^T (n-2k) d_{j}(k)$

(10)

Pre výpočet c_j(k) a d_j(k), J≤j≤-1 potrebujeme určiť iba koeficienty c₀(n) zo vzoriek signálu f(t). Imlementácia priamej DMWT a spätnej DMWT pomocou banky vektorových filtrov ako aj vektorových decimátorov a interpolátorov pre pre jednu úroveň je na obr. 1.

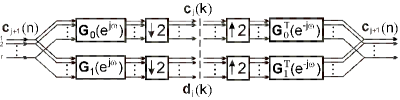
Obr. 1. Imlementácia priamej a spätnej DMWT pre j-tu úroveň.

Implementácia úplnej priamej DMWT je na obr. 2 a úplnej spätnej DMWT na obr. 3.

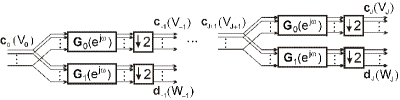
Obr. 2. Implementácia úplnej priamej DMWT.

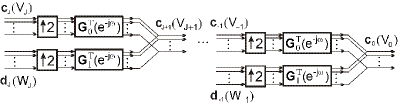
Obr. 3. Implementácia úplnej spätnej DMWT

Každý vektorový filter na obr. 1 pre jednu úroveň priamej a spätnej DMWT s r=2 má dva vstupy a dva výstupy.

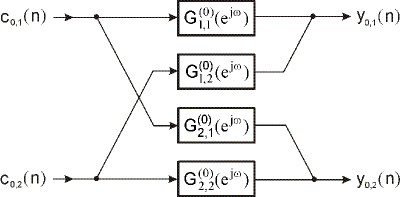
Obr. 4. Vektorový filter s $G_0(e^{j \omega})$ pre r=2 je zložený zo skalárnych filtrov s $G_{1,1}^{(0)}(e^{j \omega}) , G_{1,2}^{(0)}(e^{j \omega}) , G_{2,1}^{(0)}(e^{j \omega}) , G_{2,2}^{(0)}(e^{j \omega})$ .

Napr. vektorový filter s maticovou komplexnou frekvenčnou charakteristikou $G_0 (e^{j \omega}) = [G_{l,m}^{(0)} (e^{j \omega})]_{2 \times 2}$ , r=2, ℓ,m=1,2, je zložený zo skalárnych filtrov s komplexnými frekvenčnými charakteristikami $G_{1,1}^{(0)}(e^{j \omega}) , G_{1,2}^{(0)}(e^{j \omega}) , G_{2,1}^{(0)}(e^{j \omega}) , G_{2,2}^{(0)}(e^{j \omega})$ ako to vidno na obr.4, kde y_0,1(n) a y_0,2(n) sú koeficienty subkanálov na výstupe tohto vektorového filtra. Analogickým spôsobom by sme mohli vyjadriť aj vektorový filter s maticou $G_1(e^{j \omega})$ a zobraziť ho s dvomi vstupmi a dvomi výstupmi. Podobne ako pri skalárnej DWT rovnako aj pri DMWT výstupné signály z DP vektorového filtra by mali byť zachované, zatiaľ čo výstupné signály z HP vektorového filtra by mali byť úplne potlačené. Vlastnosť potlačenia na výstupe HP vektorového filtra závisí na ráde aproximácie. DMWT má rád aproximácie R, ak všeobecne pre momenty jej waveletových funkcií platí [9]

$\int t^m \psi_i (t) dt =0, \; 0 \leq i \leq r-1 \, \text{a} \, 0 \leq m \leq R-1$

(11)

potom pre r=2

$\int t^m \psi_i (t) dt =0, \; i=1,0 \, \text{a} \, 0 \leq m \leq R-1$

(12)

Keď DMWT má rád aproximácie R, potom za predpokladu, že vstupné signály do HP vektorového filtra sú diskrétne polynomiálne signály, výstupné polynomiálne signály (spektrálne koeficienty v tvare polynomiálnych diskrétnych funkcií) rádu menšieho ako R budú potlačené. Avšak vo všeobecnosti pre DMWT vlastnosť zachovania polynomiálnych signálov na výstupe DP vektorového filtra automaticky nevyplýva z vlastnosti nulových momentov. Keď na výstupe DP sú zachované polynomiálne signály, potom daná DMWT je frekvenčne vyvážená. Rád vyváženia je p, ak na výstupe DP vektorového filtra DMWT sú zachované, resp. na výstupe HP vektorového filtra DMWT sú potlačené všetky polynomiálne signály rádu menšieho než p ( $p \leq R$ ). DMWT, ktoré nevyhovujú vlastnosti zachovania/potlačenia diskrétnych polynomiálnych signálov sa nazývajú nevyvážené.

3. DMWT s prefiltráciou a postfiltráciou

Jednou z dôležitých úloh pri aplikovaní DMWT je úloha jej inicializácie (prefiltrácie), keď je potrebné na začiatku obvykle existujúci iba jeden vstupný skalárny (jednorozmerný) signál f(n) pretransformovať vhodným spôsobom na r-rozmerný vstupný vektorový signál, ktorým je postupnosť vektorov začiatočných koeficientov c₀(n) = [c_0,1(n),…,c_0,r(n)]^T. Operácia pomocou ktorej sa táto transformácia vykoná sa nazýva prefiltrácia A a realizovaná je prefiltrami. Príslušnú postfiltráciu je potom potrebné vykonať po spätnej DMWT a musí to byť inverzný proces k prefiltrácii. Operácia postfiltrácie B sa vykonáva v postfiltroch a musí vyhovovať podmienke AB = I , kde I je filtrácia identity. Preto, ak použijeme prefiltráciu A, DMWT, DMWT^-1 a postfiltráciu B pre vstupný signal f(n), ako to vidno na obr. 5, potom výstupný signál $\hat{f}(n)$ z tejto kaskády bude identický so vstupným signálom.

Obr. 5. Bloková schéma DMWT a IDMWT^-1 s prefiltrom a postfiltrom.

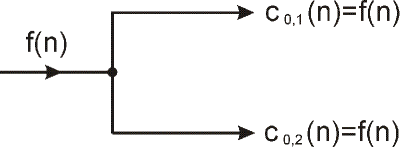
Pre frekvenčne nevyvážené vektorové filtre DMWT existuje niekoľko metód návrhu prefilrov [10]. Vhodnou prefiltráciou sa v tomto prípade kompenzuje nedostačujúca vlastnosť zachovania/potlačenia signálov, resp. mierkových a detailových koeficientov ako bolo už vyššie uvedené. Druh použitej prefiltrácie je rozhodujúci pre získanie dobrých výsledkov pre určitú aplikáciu DMWT. Ďalej sú uvedené štyri základné spôsoby prefiltrácie bez spojenia s konkrétnou DMWT. Najjednoduchším spôsobom prefiltrácie pre r=2 je ten, že sa ako vstupné signály pre DMWT použijú identické signály rovné vstupnému skalárnemu signálu f(n) s rovnakou dĺžkou N, t.j.

$c_{0,1}(n) = c_{0,2}(n) = f(n)$

(13)

ako to vidno na obr. 6

Obr. 6 Spôsob prefiltrácie

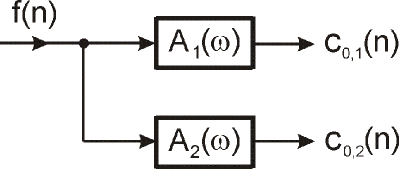
Druhý spôsob prefiltrácie je na obr. 7, kedy sú použité dva filtre s amplitúdovými frekvenčnými charakteristikami A₁(ω), A₂(ω),

Obr. 7 Spôsob prefiltrácie

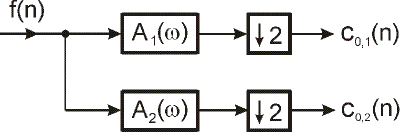
Pri treťom spôbe prefiltrácie sú za filtre A₁(ω), A₂(ω) zaradené decimátory ako to vidíme na obr. 8.

Obr. 8 Spôsob prefiltrácie

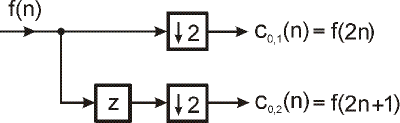
Vyššie uvedené spôsoby prefiltrácie môžu byť zovšeobecnené pre ľubovoľné r. V štvrtom spôsobe prefiltrácie pre r=2 sa jedná o rozdelenie vstupného skalárneho signálu f(n) na postupnosť párnych a nepárnych vzoriek, t. j.

$\left [ \begin{array}{c} c_{0,1}(n) \\ c_{0,2}(n) \end{array} \right ] = \left [ \begin{array}{c} f(2n) \\ f(2n+1) \end{array} \right ]$

(14)

čo je možné realizovať blokovou schémou podľa obr. 9.

Obr. 9 Spôsob prefiltrácie

DMWT s prefiltrami na obr. 6 a 7 sa nazývajú redudantné a DMWT na obr. 8 a 9 neredudantné s maximálnou decimáciou.

4. DMWT s DGHM multiwaveletmi

Jednou z najznámejších DMWT s násobnosťou r=2 je DMWT navrhnutá Donovanom, Geronimom, Hardingom a Massopustom [6]. Koeficienty g₀(k) a g₁(k) sú matice rozmeru 2×2, t.j.

$g_0(0) = \left [ \begin{array}{cc} \frac{3}{10} & \frac{2\sqrt{2}}{5} \\ \frac{-\sqrt{2}}{40} & \frac{-3}{20} \end{array} \right ] , \; g_0(1) = \left [ \begin{array}{cc} \frac{3}{10} & 0 \\ \frac{9\sqrt{2}}{40} & \frac{1}{2} \end{array} \right ]$

$g_0(2) = \left [ \begin{array}{cc} 0 & 0 \\ \frac{9\sqrt{2}}{40} & \frac{-3}{20} \end{array} \right ] , \; g_0(3) = \left [ \begin{array}{cc} 0 & 0 \\ \frac{-\sqrt{2}}{40} & 0 \end{array} \right ]$

(15)

$g_1(0) = \left [ \begin{array}{cc} \frac{-\sqrt{2}}{40} & \frac{-3}{20} \\ \frac{-1}{20} & \frac{-3\sqrt{2}}{20} \end{array} \right ] , \; g_1(1) = \left [ \begin{array}{cc} \frac{9\sqrt{2}}{40} & \frac{-1}{2} \\ \frac{9}{20} & 0 \end{array} \right ]$

$g_1(2) = \left [ \begin{array}{cc} \frac{9\sqrt{2}}{40} & \frac{-3}{20} \\ \frac{-9}{20} & \frac{3\sqrt{2}}{20} \end{array} \right ] , \; g_1(3) = \left [ \begin{array}{cc} \frac{-\sqrt{2}}{40} & 0 \\ \frac{1}{20} & 0 \end{array} \right ]$

(16)

Mierkové a waveletové funkcie (bázové funkcie) tejto DMWT poskytujú kombináciu ortogonality, symetrie a krátkeho nosiča, čo nemôže byť dosiahnuté pomocou žiadnej skalárnej waveletovej bázy (žiadnej skalárnej DWT). Mierkové a waveletové funkcie pre DGHM DMWT sú na obr. 10.

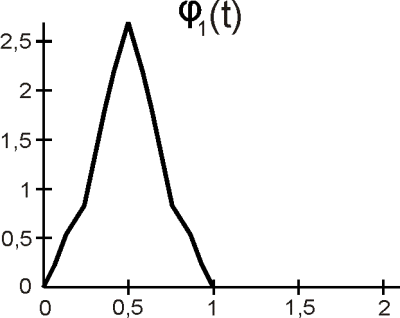
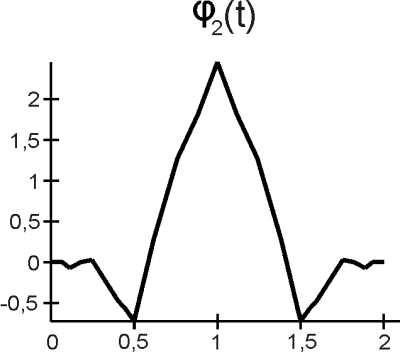
(a)

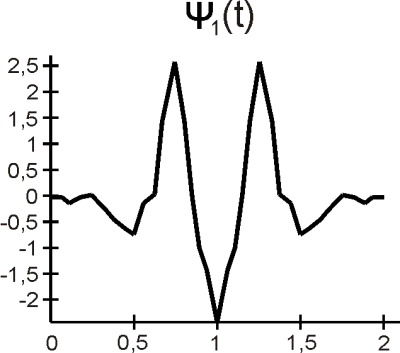
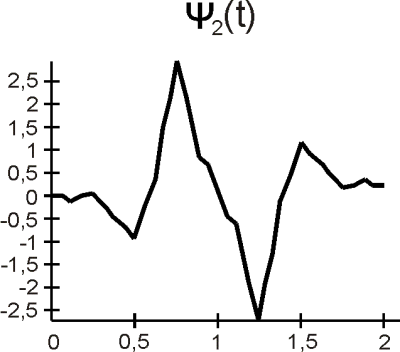
(b)
Obr. 10. a) Mierkové $\varphi_1 (t)$ a $\varphi_2 (t)$ , b) waveletové $\psi_1 (t)$ a $\psi_2 (t)$ funkcie.

Obidve mierkové funkcie $\varphi_1 (t)$ , $\varphi_2 (t)$ sú symetrické a trvajú na krátkom suporte <0, 1>, <0, 2>. Waveletová funkcia $\psi_1 (t)$ je párna, $\psi_2 (t)$ nepárna a trvajú na rovnakom krátkom suporte <0, 2>. DGHM DMWT má rád aproximácie R=2, ale na druhej strane rád vyváženia p = 0. Na rozdiel od klasickej DWT vstupný (pôvodný) skalárny signál musí byť transformovaný na vektorový tvar pred vykonaním samotnej priamej DMWT a musí byť obnovený z vektorového tvaru po vykonaní spätnej DMWT na skalárny signál pre danú aplikáciu.

5. Implementácia DMWT s DGHM multiwaveletmi

Na základe koeficientov g₀(k) a g₁(k) a rov.(3) môžeme vyjadriť pre DP a HP multifiltre komplexné frekvenčné charakteristiky skalárnych filtrov a im zodpovedajúce impulzné charakteristiky s ich vlastnosťami dĺžky a párnosti nasledovne:

Pre DP multifilter

$G_1^0 (e^{j \omega}) = G_{1,1}^0 (e^{j \omega}) \rightarrow g_1^0 (n) = \left \{ \frac{3}{10}, \frac{3}{10} \right \}$

, dĺžka párna, symetria párna

$G_2^0 (e^{j \omega}) = G_{2,1}^0 (e^{j \omega}) \rightarrow g_2^0 (n) = \left \{ \frac{2\sqrt{2}}{5} \right \}$

, dĺžka nepárna, symetria párna

$G_3^0 (e^{j \omega}) = G_{1,2}^0 (e^{j \omega}) \rightarrow g_3^0 (n) = \left \{ \frac{-2\sqrt{2}}{40}, \frac{9\sqrt{2}}{40}, \frac{9\sqrt{2}}{40}, \frac{-2\sqrt{2}}{40} \right \}$

, dĺžka párna, symetria párna

$G_4^0 (e^{j \omega}) = G_{2,2}^0 (e^{j \omega}) \rightarrow g_4^0 (n) = \left \{ \frac{-3}{20}, \frac{1}{2} , \frac{-3}{20} \right \}$

, dĺžka nepárna, symetria párna

Pre HP multifilter

$G_1^1 (e^{j \omega}) = G_{1,1}^1 (e^{j \omega}) \rightarrow g_1^1 (n) = \left \{ \frac{-\sqrt{2}}{40}, \frac{9\sqrt{2}}{40}, \frac{9\sqrt{2}}{40}, \frac{-\sqrt{2}}{40} \right \}$

, dĺžka párna, symetria párna

$G_2^1 (e^{j \omega}) = G_{2,1}^1 (e^{j \omega}) \rightarrow g_2^1 (n) = \left \{ \frac{-3}{20}, \frac{-1}{2} , \frac{-3}{20} \right \}$

, dĺžka nepárna, symetria párna

$G_3^1 (e^{j \omega}) = G_{1,2}^1 (e^{j \omega}) \rightarrow g_3^1 (n) = \left \{ \frac{-1}{20}, \frac{9}{20}, \frac{-9}{20} \frac{1}{20} \right \}$

, dĺžka párna, symetria nepárna

$G_4^1 (e^{j \omega}) = G_{2,2}^1 (e^{j \omega}) \rightarrow g_4^1 (n) = \left \{ \frac{-3\sqrt{2}}{20}, 0 , \frac{3\sqrt{2}}{20} \right \}$

, dĺžka nepárna, symetria nepárna

Na obr. 11 sú zobrazené príslušné skalárne filtre dané ich impulznými charakteristikami v DP multifiltri

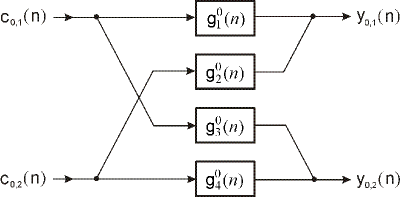
Obr. 11 Skalárne filtre pre DP multifilter.

a na obr. 12 v HP multifiltri

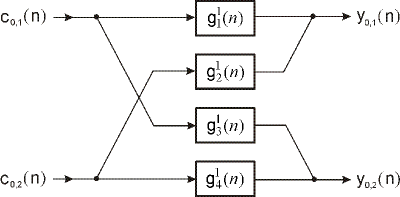
Obr. 12 Skalárne filtre pre HP multifilter.

Pretože signály c_0,1(n), c_0,2(n) z prefiltra sú konečnej dĺžky, mohlo by vo výpočítanej konvolúcii s príslušnými impulznými charakteristikami skalárnych filtrov dochádzať k nežiadúcemu skresleniu (border distortion) na jej hraniciach. Aby sme toto skreslenie eliminovali budeme signály c_0,1(n), c_0,2(n) predlžovať dvomi druhmi symetrického predĺženia. Prvý druh je celovzorkové symetrické predĺženie (WSS-Whole-sample symmetric) a druhý je polvzorkové symetrické predĺženie (HSS-Half-sample symmetric) [11]. V princípe sú obidva druhy predĺženia možné aj nepárnym spôsobom, avšak pre nami zvolenú DMWT s DGHM multiwaveletmi bude použitý prvý spôsob. Napr. pre zvolený signál x(n)= {1,2,3,4,5,6,7,8}, DP filter g₄⁰(n) je na obr. 13 zobrazené predĺženie x(n) celovzorkové párne o 3 vzorky.

xpredl = [4 3 2 1 2 3 4 5 6 7 8 7 6 5]; n = -3:10; stem(n, xpredl) xlabel('n')

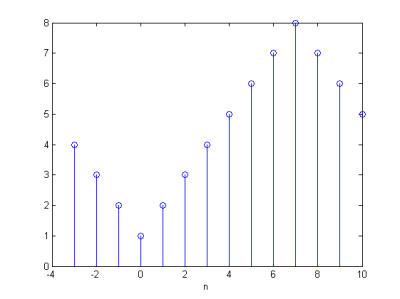
Obr. 13 Predĺženie x(n) celovzorkové párne o 3 vzorky.

a pre DP filter g₃⁰(n) je na obr. 14 zobrazené predĺženie x(n) polvzorkové párne o 4 vzorky.

xpredl = [4 3 2 1 1 2 3 4 5 6 7 8 _{8 7 6 5}]; n= -4:11; stem(n,xpredl) xlabel('n')

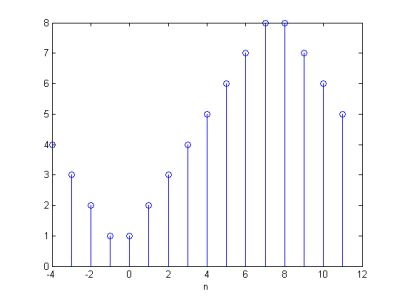
Obr. 14 Predĺženie x(n) polvzorkové párne o 4 vzorky.

Možné spôsoby predĺženia a vlastnosť konvolúcie pre rôzne kombinácie symetrie a dĺžky impulzných charakteristík skalárnych filtrov DP a HP multifiltrov sú uvedené v tab. 1.

Tab. 1

Spôsob	Pedĺženie Signálu	Filter		Konvolúcia
Spôsob	Pedĺženie Signálu	Symetria	Dĺžka	Konvolúcia
1	párne celovzorkové	párna	nepárna	párna celovzorková
2	párne polvzorkové	párna	párna	párna celovzorková
3	párne celovzorkové	nepárna	nepárna	nepárna celovzorková
4	párne polvzorkové	nepárna	párna	nepárna celovzorková

Z tab. 1 vyplýva, že môžu nastať v podstate dva spôsoby predĺženia a to párne celovzorkové a párne polvzorkové. Ako príklad je ďalej uvedený výpočet konvolúcie pre párne celovzorkové predĺženie signálu c_0,2(n) z prefiltra s impulznou charakteristikou g₄⁰(n) DP filtera.

c_0,2(n) = {4, 3, 2, 1, 2, 3, 4, 5, 6, 7, 8, 7, 6, 5} = {c_0,2(-3), c_0,2(-2), c_0,2(-1), c_0,2(0), c_0,2(1), c_0,2(2), c_0,2(3), c_0,2(4), c_0,2(5), c_0,2(6), c_0,2(7), c_0,2(8), c_0,2(9), c_0,2(10)}, g₄⁰(n) = {-0.15, 0.5, -0.15} = {g₄⁰(-1), g₄⁰(0), g₄⁰(1)}

Potom konvolúcia

$y(k) = \sum_{n-k-1}^{k+1} g_4^0 (k-n) c_0 (n), \; k=-2, -1, \dots , 9$

(17)

y(k)= {0,6; 0,4; -0.1; 0,4; 0,6; 0,8; 1; 1,2; 1,4; 1,9; 1,4; 1,2}

Grafické zobrazenie konvolúcie je na obr. 15

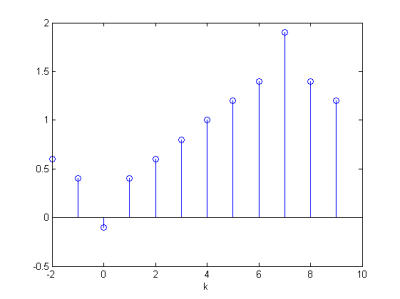
Obr. 15 Konvolúcia y(k), párna celovzorková.

Princíp výpočtu signálov na výstupoch skalárnych filtrov je na obr. 16

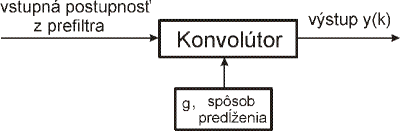
Obr. 16. Princíp výpočtu diskrétnej konvolúcie na výstupe skalárneho filtra.

Vstupná postupnosť c_0,1(n) alebo c_0,1(n) z prefiltra sa pre daný skalárny filter g predĺži spôsobom podľa tab. 1. Pre DP multifilter a jemu zodpovedajúce skalárne filtre sa vypočítajú odozvy y_0,1(k), y_0,2(k) takto

$y_{0,1}(k) = \sum_n g_1^0 (k-n) c_{0,1}(n) + \sum_n g_2^0 (k-n) c_{0,2}(n)$

$y_{0,2}(k) = \sum_n g_3^0 (k-n) c_{0,1}(n) + \sum_n g_4^0 (k-n) c_{0,2}(n)$

(18)

Tieto signály sa následne musia upraviť na dĺžku, ktorú mali signály na vstupoch DP multifiltra pred predĺžením. Analogicky sa vypočítajú odozvy y_0,1(k), y_0,2(k) na výstupoch HP multifiltra s následnou úpravou ich dĺžok. Nakoniec sú odozvy na výstupoch HP a DP multifiltrov decimované s faktorom 2, výsledkom čoho budú mierkové c_-1(k)=[c_-1,1(k), c_-1,2(k)]^T a detailové d_-1(k) = [d_-1,1(k), d_-1,2(k)]^T koeficienty priamej DGHM DMWT na prvej úrovni. Pri výpočte mierkových a detailových koeficientov na ďalších úrovniach, t.j. pre J≤j≤-1 postupujeme analogicky.

6. Záver

Nami navrhnutý spôsob implementácie DMWT s DGHM multiwaveletmi je možné všeobecne použiť aj pre iné typy DMWT. Pritom bol použitý spôsob prefiltrácie používajúci rozdelenie vstupného signálu na postupnosti párnych a nepárnych vzoriek. Podľa aplikácie kde bude použitá zodpovedajúca DMWT možno navrhnúť aj iný typ prefiltra. Pri implementácii DMWT je použitá diskrétna konvolúcia vstupných symetricky predĺžených signálov s impulznými charakteristikami štyroch skalárnych filtrov dolnopriepustného aj hornopriepustného multifiltra.

Literatúra

K. Rajakumar, T. Arivol, “Implementation of Multiwavelet Transform coding for lossless image compression“, International Conference on (ICICES), 2013, p. 634 – 637.
X. Wang, “Image De-noising Based on Multi-wavelet International Forum on Information Technology and Applications“, 2009, Vol. 3, p. 523 – 525.
T.T. Yang, F. Li, “Image watermarking algorithm based on discrete multiwavelet transform. Computer Engineering and Applications“, 2007, Vol. 43, No. 30, p. 111–115.
J. Zavacký, J. Mihalík, I. Gladišová, “Implementácia diskrétnej waveletovej transformácie v štandarde JPEG-2000“ ,Slaboproudý obzor, 2007, roč. 63, č. 3–4, str. 5–9.
F. Keinert “Wavelets and Multiwavelets“ ,Champan & Hall/CRC, 2004, ISBN 1-58-488-304-9.
G. Donovan, J.S. Geronimo, D.P. Harding, Massopust, P.R. “Construction of Orthogonal Wavelets Using Fraction Interpolation Functions“, SIAM J. Math. Anal., 1996, Vol. 27, p. 1158-1192.
C.L. Chui, J.Lian, “A Study on Orthonormal Multiwavelets“, Appl. Numer. Math., 1996, Vol. 20, p. 273–298.
X.G. Xia, “A New Prefilter Design for Discrete Multiwavelet Transforms“, IEEE Trans. On Signal Process. “, 1996, Vol. 46, No. 6, p. 1558–1570.
J. Mihalík, J. Zavacký “Diskrétne spracovanie signálov“, LČSOV FEI TU Košice, 2011, ISBN 978-80-553-0730-5, (306) strán.
S. Hongli, C. Yuanli, Q. Zulian, “On Design of Multiwavelet Prefilters. Applied Mathematics and Computation“, Vol. 172, 2006, p. 1175-1187.
A. Tinku, S.T. Ping “JPEG2000 Standard for Image Compression, Concepts, Algorithms and VLSI Architectures“, John Wiley & Sons, 2005.

Spoluautorom článku je prof. Ing. Ján Mihalík, PhD., Katedra elektroniky a multimediálnych telekomunikácií, FEI TUKE, Slovenská republika

O časopise

Meta

RSS

Diskrétna multiwaveletová transformácia a jej implementácia s DGHM multiwaveletmi

Napísať príspevok

Rubriky

Burza práce

Štúdijné materiály

Archív