Heat transfer model of building calibrated by genetic algorithm
14. September, 2009, Autor článku: Števo Stano, Elektrotechnika, MATLAB/Comsol
Ročník 2, číslo 9  Pridať príspevok
Pridať príspevok
 In the article is presented the calibration process of building model by genetic algorithm. The genetic algorithm finds the best combination of model structural parameters with regard to attain the best correspondence between simulation and real data. Genetic algorithm was created in Matlab and simulation in Comsol Multiphysics.
In the article is presented the calibration process of building model by genetic algorithm. The genetic algorithm finds the best combination of model structural parameters with regard to attain the best correspondence between simulation and real data. Genetic algorithm was created in Matlab and simulation in Comsol Multiphysics.
Introduction
The proposal task of the optimal heating subsystem is not trivial. Nowadays designers use a lot of software as a support for the proposal process of heating systems. In this case is important to have the most precise model to attain the best results from simulations (to attain the maximum correspondence between data from simulation and data from real world). The model complexity depends on prescribed precision and on the amount of considered factors, which have influence on followed quantity. It is natural, that between model (mathematical, physical, computer etc.) and real object is always some discrepancy. This difference can be reduced by many manners. We decided to use genetic algorithm due to some advantages, which are suitable for this kind of problem.
Validation
If a model is used to system analyze, it is very important to know the inner representation of individual physical processes, which are significant for examined system. Without mentioned understandings are impossible to interpret correctly the inconformity between measured data and data from simulation. To eliminate this inconformity is needed to realize validation process of experiment, which is depicted in figure 1.

Fig. 1 Principle of validation process
Where is the fault?
In general, if a significant discrepancy between real and simulated data was detected, the technical structure of the model is the last of the factors, where the fault is expected. The most common faults are:
- non adequate model (amount of factors)
- non adequate calibration
- bugs in the program code
- faults in inputs
- wrong compilation of simulation
- bad experimental data
Our goal is to adjust our (geometrical) model (find the best combination of structural model parameters), therefore is obvious that simulation discrepancy rise in a) group with consideration of precondition of correctness of program, inputs, simulation compilation and simulation result interpretation.
Calibration process
Model
The goal is to propose optimal heating subsystem, therefore the model has to include all significant parameters (thermal conductivity, density, heat capacity etc.) which influence followed physical quantity (heat transfer). Fig. 2 shows 3D model of a flat (peripheral walls, screens, insulation, window, door etc.).
Presume that physical properties of construction parameters are defined correctly (in practice it is so, because this data are measured and written in tables of materials and their fluctuations are insignificant low in comparison with other parameters), then it is obvious, that the calibration will be done by modifying of structural parameters (e.g. thickness of walls, insulation layer etc.) and ambient temperature from predefined intervals (Hantuch, 2003).
In our case (3 rooms flat) it is parametric model with next parameters: thicknesses of walls, screens, insulation layer, windows, doors and temperature of ceiling and floor. Due to the fact that the parameters influence on the simulation result is not exactly described, we decided to calibrate mentioned model by genetic algorithm. The simulation is initial point for genetic algorithm.
Simulation
We can use this 3D model in various simulation software, which allow simulating a heat diffusing process in materials. We decided for program Comsol Multiphysics due to many advantages in comparison with the other programs. Comsol is a new version of former FemLab 3.3. As the name betray, the solving of physical process is based on FEM (Final Element Method).
This tool allows solving the task (in one step) from many physical aspects (e.g. temperature variation in dependence on electric current of conductor and the influence of this variation on mechanical conditions of conductor). Another advantage is its simple connectivity to MatLab and possibility to import 3D models from many programs, one of them is Catia V5. We just import model from Catia into Comsol and we save a lot of time, because the process of model creation in Comsol is not easy. Before the launching of simulation we have to do next actions:
- to set properties of Sub-domains
- to set properties of boundary surfaces
- to create Mesh for FEM solver

Fig. 3 Setting process of Sub-domains
Genetic algorithm
Genetic algorithm (GA) is a heuristic method, which strives to find the solution of complex problems (for which doesn’t exist exact algorithm) by application of principles of evolution biology. Genetic algorithms and all methods which belong among evolution algorithm use techniques which imitate processes of evolution which are well-known in biology – heredity, mutation, natural selection and crossing. (Sekaj, 2005)
The principle of GA is the consecutive production various solutions of given problem. During the solution process is kept so-called population. This population consists of terms and each term is one solution of given problem. As the population goes through the evolution, the solutions get better. Traditionally is solution represented by binary numbers (strings of zeros and ones) but also by other representations (tree, field, matrix, etc.). Typically is at the beginning of GA (on the first generation) created population which is compounded from completely random terms. At the transition to the new generation for each term is counted so-called fitness. This fitness represents the quality of solution which represents the term. According to this quality are selecting (by stochastic, random or another type of the selection) the individuals which are modified (by mutation and crossing), what with is created new population. This procedure is repeated iteratively and will stop when the solution will reach the desired quality or after given time.
Process of GA creating
As was mentioned, GA solves (finds) the optimal construction parameters in order to attain the best correspondence between real and simulated data. We additionally defined 60 points (in outer surface and in each room). In these points are evaluated the temperature and this data are inputs to fitness of GA. Genetic algorithm was created in Matlab (Foltin, 2008) by using genetic toolbox, which was created at FEI STU.
String
As was mentioned before, the calibration is adjusting seven parameters (thickness of walls, screens, insulation layer, windows, doors and temperature of ceiling and floor). The midpoints of intervals were set as real measured values and the sizes of intervals were set as < -5%, +5%>. From these assumptions the string has 22 genes. Each gene represents thickness of independent element (e.g. south wall, living room screen etc.)
Population
By GA we are looking for 22 parameters, therefore is sufficient if the population has 50 terms. We decided to use selection by balanced roulette wheel with elitist property (the best individual goes to the next population without any change).
Fitness
The quality of solution is considered as the correspondence between measured and simulated data. For each room is count average temperature and from this value is subtract measured value, which was measured in corresponded rooms. The sum of absolute values of all subtracts is the value of fitness.
Parameters of evolution
GA uses one point crossing, additive mutation (max. value is 0.1) with the rate 0.25 and mutation on random value with the same rate (0.25). Rate is from interval <0, 1> and this value represents the occurrence off mutations in the population.
Number of generation
Due to the fact that we are looking for 22 parameters and the computational demands are very high, we set the stop condition of GA on 1000 generations. As we found from results, this amount is sufficient (the fault decreased for many times).
The solution
at the end of 1000th generation – one room for better illustration
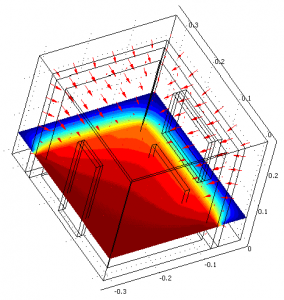
Fig. 4 The solution at the end of 1000th generation
Main results
The measurement was done during the December 2008 and it had to respect some conditions. The three days weather has to be stable (demands building dynamic), gloomy weather is better (minimize thermal gain), day without wind (minimize differences in temperature between windward and windless walls) and stable heating process. All temperature measurements were done by touch thermometer GTH 175/Pt GES. Simulation without calibrated model proves next faults -2.12 °C, -2.01 °C, -1.97 °C, -1.90 °C, -1.85 °C, -1.63 °C.
This difference is count as Td = Ts – Tm , where Ts is value from simulation and Tm is measured temperature. The fault is determined by relation: Err= |Td| / Tm [%]. The maximum error is 9.6 %. The simulation with calibrated model proves faults -0.74 °C, -0.66 °C, -0.64 °C, -0.60 °C, -0.58 °C, -0.21 °C. The maximum error is 3.4 %. It is obvious that simulation with calibrated model has less error so the calibration process has significant influence on simulation result.
Conclusion
On the simple example were showed the possibilities which allow mutual interconnection of MatLab and Comsol Multiphysics. By the genetic algorithm were found optimal structural parameters of 3D model, with fulfillment of prescribed conditions. The first simulation (without calibration) covered real data on 90% (the fault was about 10%).The last simulation (the best solution at the 1000th generation) proves 97% agreement with the real measured data, so the significance of calibrating is obvious. The amount of parameters needed for simulation of more complex objects (e.g. heating system of whole house) grows considerable and also grows the time needed for one simulation in Comsol (for bigger objects we have bigger mesh, i.e. more points for FEM solver). If we consider also the building construction (thermal/insulation properties from the point of heating) the string length of GA will be count in tens.
With the amount of parameters also grows the population of GA and the number of needed generations. If we assume that one simulation takes about few tens of seconds (on one processor unit) the resultant time for whole computation process can easily reach on few days (months). Therefore is necessary to involve only significant parameters. All in all if we want to reach the acceptable computing time of more complex solutions, is needed to use multiprocessor unit or net of computers.
- Foltin, M. (2008). Matlab – nástroj pre vedu a techniku, ATP 3/2008, pg. 58
- Hantuch, I., (2003). Simulacia a modelovanie vo virtualnej realite, International conference FM , Bratislava
- Sekaj, I., (2005). Evolučné výpočty a ich využitie v praxi, IRIS Bratislava
Co-authors of this paper is A. Šlezárová, Slovak University of Technology, Faculty of Electrical Engineering and Information Technology, Ilkovičova 3, 812 19 Bratislava.


