MEASUREMENT OF THE ENERGY ANSORPTION CAPABILITY OF POLYURETHANE FOAM
08. Marec, 2010, Autor článku: Goga Vladimír, Elektrotechnika, Prírodné vedy, Študentské práce
Ročník 3, číslo 3  Pridať príspevok
Pridať príspevok
 The influence of foam density on the energy absorption capability was studied. Impact test was performed on the specimens of polyurethane foam with various densities. Simple mechanism for impact test was constructed. Maximum stress and deformation of each specimen were compared with the results from analyses of static compression stress-strain curves.
The influence of foam density on the energy absorption capability was studied. Impact test was performed on the specimens of polyurethane foam with various densities. Simple mechanism for impact test was constructed. Maximum stress and deformation of each specimen were compared with the results from analyses of static compression stress-strain curves.
1 INTRODUCTION
Foams are a class of material with unique properties and applications. They are lightweight and designed to undergo very large deformations. They are typically used in packing and to absorb energy. Their properties are the results of the foam microstructure, a complex three-dimensional network, of struts and, possibly, membranes, which undergo large deformations and contact during deformation [1].
Energy-absorbing polymeric foams are widely used in the automotive industry to prevent injuries to the occupants in the event of front or side collisions. The use of foamed materials results in a significant improvement in the passive safety of the vehicle, owing to their excellent energy dissipation properties. In addition, they have low apparent density and are relatively cheap, allow great design flexibility, as they can be easily modeled in complex geometric parts. Typical applications include seat cushions, bumper systems, instrument panels and side protection systems. Effort is currently underway to minimize occupant head injury during an impact. The severity of injuries can be prevented or at least mitigated by the use of structural foams as cushioning.
An optimum energy-absorbing material needs to dissipate the kinetic energy of the impact while keeping the force on it below some limit, thus, resulting in a no-dangerous deceleration on the occupants. The design of effective cushioning involves many other considerations, like the shape of the protective structure, which influences load transfer during impact, and the capacity to absorb elastic energy, which controls rebound. Polymeric foams are well suitable for this kind of applications. They can undergo large compressive deformations and absorb considerable amounts of specific energy. Energy W is dissipated through the cell bending, buckling of fracture, but the stress is generally limited by the long and flat plateau of the stress-strain curve (Fig. 1). This behavior explains the high-energy efficiency that can be obtained with foamed materials. Moreover, for the same amount of dissipated energy, the foam specimen always gives a maximum force lower than the corresponding solid specimen of equal volume made of material from which the foam is derived [2].
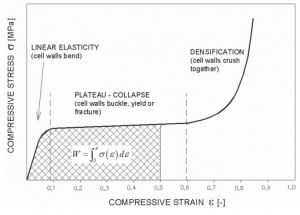
Fig. 1 The typical shape of the compressive stress-strain curve for foam
2 ENERGY ABSORPTION
Foams and honeycomb structures are used in energy absorbing structures. The possibility of controlling the sress-strain behaviour by an appropriate selection of matrix material, cellular geometry and relative density makes foams an ideal material for such applications. Decisive for the quality of packing protections or energy absorbers is the feature of being able to absorb energy without the maximum stress or the highest occuring acceleration exceeding the upper limit at which damages or injuries occur.
The aim of packing or schock absorbing is to dissipate the kinetic energy of the impact mass while keeping the maximum force (or acceleration) below some limit. For each application, a foam with optimum value of density can be found. If the density is too low, the densification zone is reached and a very high force is obtain before all the energy has been dissipated, while, if the density is too high, the force exceeds the critical value before enough energy has been absorbed, while the material compressive strain remain only partially utilized [11]. This idea can be understood by observing the graph of Fig. 2 [12]. In this figure, the stess-strain curves of three foam are compared. The hashed area under each curve corresponds to the same amount of energy absorbed, the maximum strain and stress levels are consequently determined [12].
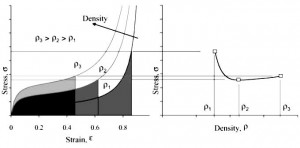
Fig. 2 Energy diagram of foams of different density
The lighter foam (with lower density ) is able to absorb the prescribed amount of energy with large deformations because there is a low-value plateau and the foam comes up to densification. On the contrary, the heavier foam (with higher density
) does absorb the same amount of energy with low deformation and high stresses. The ideal foam is that with intermediate density
. The maximum stresses that are reached by the three foams to absorb the same prescribed amount of energy it is possible to determine the optimal density for the application [12].
An energy-absorbtion diagram is better apply the idea herein explained [11]. This diagram is obtianed by plotting the absorbed energy W as a function of stress. The absorbed energy (which is the area under the stress-strain curve) is simply:
| (1) |
3 COMPRESSION TEST OF POLYURETHANE FOAM
Uniaxial compression test was performed for open-cell rigid polyurethane (PUR) foam with densities 32, 40, 50, 60, 100 and 145 kg/m3. Testing foam is used as a heat insulation and construction material (foam core sandwich panels).
Mechanical properties were evaluated as a function of foam density using a conventional mechanical test frame. Tests were conducted at an initial strain rate 0,02 s-1 and at room temperature. Deformation and acting force was measured by position sensor and compression load cell. For each density was cut one specimen with dimensions 50x50x30 mm. Fig. 3 shows stress-strain () curves of PUR foams.
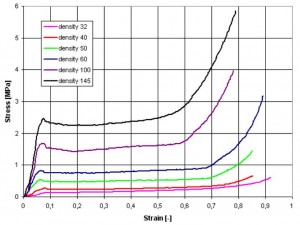
Fig. 3 Compressive stress-strain curves of PUR foams
For calculation of absorbed energy, it is necessary to approximate stress-strain curves by any equation . Phenomenological foam model (2) was used for fit the
curves (Goga, …). Model parameters for measured foams are in Tab. 1.
| (2) |
Tab 1. Model parameters
| foam density [kg/m3] | k [MPa] | c [MPa] | kP [MPa] | n [ – ] | |
|---|---|---|---|---|---|
| 32 | 2,276 | 0,115 | 0,13 | 0,074 | 4 |
| 40 | 6,817 | 0,222 | 0,085 | 0,073 | 6 |
| 50 | 16,46 | 0,465 | 0,085 | 0,176 | 6 |
| 60 | 21,9 | 0,71 | 0,086 | 0,369 | 6 |
| 100 | 45,68 | 1,481 | 0,09 | 1,181 | 6 |
| 145 | 60,485 | 2,25 | 0,1 | 2,25 | 4 |
4 IMPACT TEST
Fig. 4 shows the mechanism for impact test. Foam specimens (dimensions 80x80x50 mm) were put on the solid base. Mass with weight 6,1 kg was free fallen onto foams from height 0,76 m. It represents 45,5 J of kinetic energy at impact. In the centre of mass was installed the 1-axis accelerometer. Fig. 5 shows measured acceleration with respect to time.

Fig. 4 Mechanism for impact test
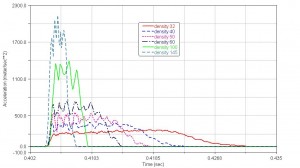
Fig. 5 Acceleration plotted against time
5 RESULTS
Each foam specimen had to absorb kinetic energy Ek> of the mass 47,87 J. It was necessary to calculate the compression if the foams during impact test for calculation the absorbed energy W from stress-strain curves. Compression was calculated in simulation program MSC.ADAMS. Simply model of the impact test was created. Input data for simulations were measured accelerations. Results of the simulations were compression values of the tested foams. Fig. 6 shows the time history of the compressions.
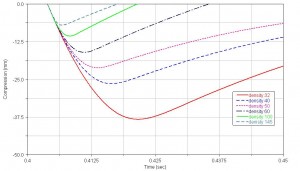
Fig. 6 Foam compression plotted against time
From maximal compressions were calculated maximal strains. Absorbed energy W was calculated by integration of equation (2). Limits of integral were 0 and calculated strains. Results of compressions, strains, calculated energies and their differences with kinetic energy are presented in Tab. 2.
Tab. 2 Results of energies
| Density [kg/m3] | Compression [mm] | Strain [-] | WM [J] | Ek [J] | |
|---|---|---|---|---|---|
| 32 | 38,26 | 76,52 | 41,71 | 47,87 | 12,9 |
| 40 | 26,43 | 52,86 | 39,12 | 47,87 | 18,3 |
| 50 | 21,16 | 42,32 | 61,23 | 47,87 | -27,9 |
| 60 | 16,05 | 32,1 | 66,99 | 47,87 | -39,9 |
| 100 | 10,64 | 21,28 | 86,1 | 47,8 | -80 |
| 145 | 7,04 | 14,08 | 75,52 | 47,87 | -57,8 |
6 CONCLUSIONS
Quasi-static compression test of PUR foam specimens with various densities were performed. Compressive stress-strain curves were obtained.
New foam specimens were subjected to impact test and the acceleration of the fallen mass was measured. Compressions of the foams during impact test were obtained by simulation of the impact test in program MSC.ADAMS.
Foams hat to absorb the all kinetic energy of fallen mass. This kinetic energy was compared with energy calculated from compressive stress-strain curves.
There are big differences, see Tab. 2. Two main reasons why there are differences can be:
- Compression of the foam is strain rate dependent. Stress-strain curves can be different for quasi-static and dynamic compression test.
- Wrong calculation of compressions and therefore energy was incorrect calculated. Monitoring compression during impact test by high speed camera is probably the best way for determining the correct values of compressions.
Behaviour of foam in respect to dynamic loading and energy absorption is object of my future study.
ACKNOWLEDGEMENT
This article has been accomplished under VEGA grant no. 1/4122/07.
REFERENCES
- Avalle, M., G. Belingardi and R. Montanini (2001). Characterization of polymeric structural foams under compressive impact loading by means of energyabsorption diagram. International Journal of Impact Engineering, vol. 25, p. 455-472.
- Brydon, A. and S. Bardenhagen (2005). Numerical Simulation of Realistic Foam Microstructures. Theoretical Division Nuclear Weapon Program Highligths, A U.S. Department of Energy Laboratory, LA-UR-05-3853.
- Gibson, L.J. and M.F. Ashby (1997). Cellular solids: structure and properties. 2nd edition, Cambridge University Press, Cambridge.
- Goga, V and B. Hučko (2008). Compression stress-strain curve modeling of cellular solids. XII. International Conference on Mechanical Engineering.
University of Technology, Faculty of Electrical Engineering and Information Technology, Ilkovičova 3, 812 19 Bratislava.

