Implementácia heuristiky pre tvorbu rozvrhu služieb vodičov autobusov pomocou pyFuzzy I.

26. November, 2010, Autor článku: Ladovský Tomáš, Informačné technológie
Ročník 3, číslo 11 Pridať príspevok

Článok sa venuje problematike rozvrhovania služieb vodičom autobusov vo verejnej autobusovej doprave. Rozvrhovaním služieb sa tu rozumie priraďovanie turnusov uvažovaným vodičom autobusov na základe ťažkých a ľahkých podmienok pre každý deň celého plánovaného obdobia napr. 28 dní.

Na riešenie problému je navrhnutá fuzzifikovaná verzia heuristickej metódy deň-za- dňom, v ktorej je neistota modelovaná pomocou fuzzy množín a riešená pomocou fuzzy logiky a fuzzy inferencie. Implementovanie neistoty je uskutočnené pomocou balíčka pyFuzzy. Navrhnutý prístup k riešeniu je overovaný na reálnej inštancií problému z MHD Martin.

1. Úvod

Problém plánovania verejnej dopravy (angl. the transportation planning prob- lem [1]) je vzhľadom na svoju komplexnosť rozdelený na niekoľko podproblémov:

Časové okná pozostávajú z jázd s príslušným časom (miestom) odchodu a príchodu. Príkladom jazdy môže byť odchod z miesta A o 9.00 a príchod na miesto B o 10.00 hodine. Súborom jázd je spoj.
Rozvrhovanie vozidiel pozostáva z prideľovania vozidiel ku turnusom. Turnus je pevne daná postupnosť spojov¹ pre jeden autobus.
Rozvrhovanie posádky pozostáva z prideľovania posádky ku vozidlám. Ide o krátkodobé plánovanie (jeden deň, niekoľko dní)
Rozpisovanie služieb posádke pozostáva z prideľovania turnusov k posádke pre dané časové obdobie. Ide o dlhodobé plánovanie (jeden mesiac alebo pol roka).

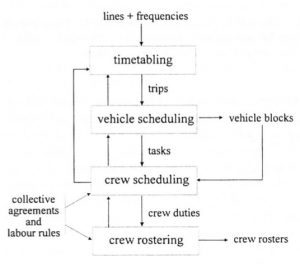
Obr. 1: Podproblémy plánovania dopravy

Vzťah medzi týmito štyrmi podproblémami je zobrazený na obrázku 1. Vo väč- šine prípadov sa tieto podproblémy vzájomne ovplyvňujú. Ak by existoval integrovaný prístup, tak by bolo plánovanie verejnej dopravy viac efektívne. Avšak z dôvodu nadmiernej komplexnosti samotných podproblémov, je takýto prístup neprípustný. Preto sa k vyriešeniu problému plánovania pristupuje sekvenčne.

Nasledujúci text sa zaoberá posledným podproblémom a to rozpisovaním služieb vodičom autobusov v danom časovom období. Problém rozpisovania služieb vodičom autobusov (angl. The Bus Driver Rostering Problem – DRP) pozostáva zo zobrazenia množiny vodičov do množiny turnusov pre každý deň danej časovej periódy. Tento problém je v článku definovaný s ohľadom na viacero právnych predpisov, ktorými stanovené podmienky musia byť dodržané.

Všetkým vodičom musíme priradiť turnus alebo deň voľna a to pre každý deň plánovaného obdobia. Preto pre každého vodiča musí tvorca rozpisu služieb vyhotoviť postupnosť turnusov a dní voľna pre uvažovanú časovú periódu. DRP je obmedzovaný viacerými právnymi predpismi [2] a pravidlami spoločností pomocou nasledujúcich ťažkých podmienok:

(h1) každý turnus musí byť pridelený maximálne jednému vodičovi;
(h2) každý vodič môže dostať pridelený maximálne jeden turnus z vopred zvolenej podmnožiny množiny všetkých turnusov (pracovné dni, víkend, sviatky, leto, zima) alebo deň voľna;
(h3) každý vodič musí odpočívať minimálne 11 hodín medzi dvoma nasledujúcimi turnusmi;
(h4) každý vodič musí mať minimálne raz za týždeň nepretržitý odpočinok dĺžky 24 hodín, ktorý musí naviac bezprostredne nasledovať po povinnom dennom odpočinku dĺžky 11 hodín. (článok sa nezaoberá);
(h5) celkový pracovný čas nesmie presiahnuť 60 hodín za týždeň (článok sa nezaoberá).

Nazývajú sa ťažkými podmienkami, pretože sa pri vytváraní rozpisu služieb nesmú porušiť. Sú predpísané právom, zmluvami a pravidlami autobusovej spoločnosti. S ohľadom na ťažké podmienky dobré rozpisy služieb obvykle obsahujú malé diferencie medzi celkovými rozvrhnutými pracovnými hodinami každého vodiča.

Ďalej je dobrý rozpis služieb charakterizovaný tým, že vodičom sa opakujú rovnaké alebo podobné turnusy vzhľadom na trasu a/alebo obtiažnosť. Pri vytváraní dobrého rozpisu služieb sa môžeme stretnúť s nasledujúcimi charakteristikami (ľahké podmienky):

(s1) zrovnomerňovaním celkových kumulovaných denných pracovných časov vodičov za celé časové obdobie rozpisovania služieb;
(s2) maximalizáciou frekvencie opakovania rovnakých alebo podobných turnusov;
(s3) maximalizáciou počtu vodičov (článok sa nezaoberá);
(s4) maximalizáciou ocenenia vodičov (článok sa nezaoberá);
(s5) minimalizáciou nákladov (článok sa nezaoberá).

V ľahkých podmienkach sú zahrnuté ciele rozpisovania služieb a tie optimalizujeme.

Vieme, že rozpisovanie služieb je komplexný a obtiažny problém a z tohoto dôvodu väčšina prístupov navrhnutých v literatúre je založená na heuristikách (zakázané prehľadávanie, metóda generovania stĺpcov, simulované žíhanie, dekompozícia, memetická heuristika, heuristika deň-za-dňom a vodič-za-vodičom). Najznámejšie oblasti rozpisovania služieb sú:

rozpisovanie služieb zdravotným sestrám [3], [4];
rozpisovanie služieb pre členov posádky leteckej dopravnej spoločnosti [5], [6] (nejde o heuristiku), [7];
rozpisovanie služieb vodičom autobusov [8], [9];
rozpisovanie služieb vodičom vlakov [10];
teoretický prístup ku problému (problém permutovania stĺpcov matice – matrix permutation problem) [11], [12], [13].

V článku [14] je problém rozpisovania služieb vodičom autobusov modelovaný pomocou zovšeobecneného problému rozkladu množín. Iný spôsob riešenia problému je pomocou metódy vodič-za-vodičom. Táto metóda najskôr nájde rozpis služieb pre prvého vodiča, potom pre druhého, atď. Jej riešenie (rozpis služieb) ale vykazuje postupne pre každého nasledujúceho vodiča čoraz väčšie nerovnomernosti v celkových pracovných časoch. Ošetrenie tohoto nedostatku by stálo veľa režíjneho času. Vzhľadom na očakávaný rozpis služieb, ktorý je obmedzovaný ťažkými a ľahkými podmienkami, sa javí ako vhodná heuristika deň-za-dňom.

Táto metóda [8] najskôr nájde priradenia medzi vodičmi a turnusmi pre prvý deň plánovaného obdobia, potom pre druhý, atď. Jej hlavný nedostatok leží v skutočnosti, že sa veľmi ťažko rozpoznávajú problémy, ktoré môžu vzniknúť v nasledujúcich dňoch. V nasledujúcom texte predpokladáme, že tento nedostatok je akýmsi neistým zobrazením množiny vodičov do množiny turnusov počas danej časovej periódy. Nasledujúca sekcia matematicky formuluje zadanie problému, definuje niekoľko parametrov rozpisovania služieb a popisuje heuristickú metódu deň-za- dňom.

2 Matematická formulácia problému

Nech D = {1,2, …,n} je množina dní, V = {V₁,V₂, …,V_m} je množiny vodičov a T = {T₁, T₂, . . . , T_t} je množina turnusov. Parameter n značí počet dní, parameter m vyjadruje počet vodičov a parameter t je počet turnusov.

Rozpisovanie služieb vodičom autobusov znamená, že pre každý deň z množiny dní D sa priradí vodičovi Vi ∈ V deň voľna alebo turnus Tk ∈ T z množiny turnusov tak, aby nedošlo k porušeniu žiadnej ťažkej podmienky počas optimalizovania ľahkých podmienok.

Turnus je definovaný usporiadanou trojicou T_k = (b_k,e_k,c_k) nasledovných parametrov: časom začatia b_k; časom ukončenia e_k a denným pracovným časom vodiča c_k turnusu T_k ∈ T. Jednotkou času sú minúty.

Nech σ_ijk je binárny parameter rozpisovania služieb, ktorý je definovaný nasledovne:

pre ∀(V_i,j,Tk) ∈ V×D×T

Nech u_ik je binárny parameter rozpisovania služieb, ktorý je definovaný nasledovne:

pre ∀(V_i,T_k)∈V×T.

Tento parameter sa dá odvodiť z parametra σ_ijk a to nasledovne:

$u_{ik} = max_{j \in D} \lbrace \sigma _{ijk} \rbrace$

Tento parameter definuje tvorcovi rozpisu služieb či môže danému vodičovi priradiť určitý turnus. Taktiež môžeme týmto parametrom definovať náročnosť turnusov, senioritu, preferovanie určitých turnusov alebo typu autobusu, a veľa iného.

Nech v_ij je binárny parameter rozpisovania služieb, ktorý je definovaný nasledovne:

pre ∀(V_i,j)∈V×D

Tento parameter sa dá odvodiť z parametra σ_ijk a to nasledovne:

$v_{ik} = max_{T_k \in T} \lbrace \sigma _{ijk} \rbrace$

Tento parameter slúži na modelovanie požadovaných dní voľna zo strany vodičov, plánované školenia zo strany zamestnávateľa, zdravotnú starostlivosť a iné.

Nech w_jk je binárny parameter rozpisovania služieb, ktorý modeluje rozhod- nutia:

pre ∀(j,T_k)∈D×T

Tento parameter sa dá odvodiť z parametra σ_ijk a to nasledovne:

$w_{ik} = max_{V_i \in V} \lbrace \sigma _{ijk} \rbrace$

Nie každý turnus sa musí odjazdiť v daný deň. Napríklad turnusy pre voľné dni sa nesmú odjazdiť cez týždeň a naopak.

Ak sú parametre u_ik, v_ij a w_jk odvodené od parametra σ_ijk, tak potom spolu tvoria iba čiastočnú informáciu, ktorú obsahoval parameter σ_ijk.

Rozpis služieb R = (x_ijk) modelujeme pomocou binárnej premennej x_ijk následovne:

pre ∀(V_i,j,T_k) ∈ V×D×T

Táto premenná vyjadruje rozhodnutia tvorcu rozpisov služieb pri prideľovani turnusov vodičom za celé obdobie.

Algoritmus deň-za-dňom je postupnosť krokov, ktorá rieši problém rozpisovania služieb tak, že najskôr priradí vodičom V_i ∈ V turnusy T_k ∈ T alebo deň voľna pre prvý deň, pričom nedôjde k porušeniu žiadnej ťažkej podmienky počas optimalizovania ľahkých podmienok. Potom pre druhý deň až nakoniec pre posledný deň plánovaného obdobia. Riešením algoritmu deň-za-dňom je suboptimálny rozpis služieb

$R^* = (x_{ijk}^*)$ pre ∀(V_i,j,T_k)∈V×D×T.

Na základe vyššie spomínaného princípu algoritmu predpokladajme, že už pre dni z množiny D_s−1 = {0,1,2,…,s−1} prebehlo rozpisovanie služieb. Potom prvý nasledujúci nespracovaný deň nazveme aktuálnym dňom a značíme ho symbolom s ∈ D. Je zrejmé, že x_ijk pre 1 ≤ j ≤ s − 1 obsahuje záznamy rozpisovania služieb (nadobúda jednotky alebo nuly), ktoré sa udiali pred aktuálnym dňom a pre s ≤ j ≤ n ešte rozpis služieb neexistuje (obsahuje samé nuly) a to pre ∀(V_i , T_k ) ∈ V × T . Dni D_s−1 nazveme predošlými dňami.

Nech s je aktuálny deň heuristiky, potom vzhľadom na predošlé dni modelujeme rozpis služieb v aktuálnom dni premennou y_ik následovne:

pre ∀(V_i,T_k)∈V×T.

Algoritmus deň-za-dňom

k1: Inicializuj aktuálny deň na prvý deň plánovaného obdobia, s ∶= 1.
k2: Pomocou vopred zvolenej metódy rozpisovania služieb v aktuálny deň získaj optimálne riešenie rozpisu služieb v aktuálnom dni Y^*.
k3: Pre daný aktuálny deň s aktualizuj rozpis služieb R, teda x_isk ∶= y^* ,∀(V_i,T_k)∈V×T
k4: Ak je aktuálny deň rovný poslednému dňu obdobia rozpisovania služieb (s = n) potom koniec, R je rozpisom služieb R^* inak prejdi na nasledujúci deň (s ∶= s + 1) a goto k2.

Metóda rozpisovania služieb v aktuálny deň je postup riešenia problému rozpisovania služieb v aktuálny deň. Riešením metódy rozpisovania služieb v aktuálny deň je optimálny rozpis služieb v aktuálnom dni

$Y^* = (y_{ik}^*)$ pre ∀(V,T)∈V×T

Ak je aktuálny deň prvým dňom, s = 1, tak pre tvorcu rozvrhu vzniknú prvé komplikácie. Buď vykoná rozpisovanie služieb s „čistým začiatkom“, čo znamená, že neberie do úvahy rozpis služieb z predošlého obdobia, alebo využije informácie zo starého rozpisu služieb a nový rozpis služieb naň nadviaže. Pre značné uľahčenie tvorby heuristiky a nedostatok miesta predpokladáme, že predošlý rozpis služieb nemáme.

Nasledujúca sekcia sa venuje tvorbe optimalizačných kritérií vzhľadom na definované ľahké podmienky v úvode článku. Ďalej sekcia ukazuje použitie mier nerovnomernosti na príkladoch.

3 Miery nerovnomernosti

V úvode článku sme definovali dve ľahké podmienky (s1) a (s2). V týchto ľahkých podmienkach sú zahrnuté ciele rozpisovania služieb a tie máme za úlohu optimalizovať. Aby sme dosiahli zrovnomernenie celkových kumulovaných denných pracovných časov vodičov za celé časové obdobie rozpisovania služieb, potrebujeme poznať mieru nerovnomernosti, ktorá by informovala tvorcu rozpisu služieb o tom, do akej miery je uvažovaný rozpis služieb nerovnomerný. Čím je miera nerovnomernosť menšia, tým sú kumulované denné pracovné časy vodičov za celé obdobie rozpisovania služieb rovnomernejšie. Preto sa snažíme mieru nerovnomernosti týkajúcu sa ľahkej podmienky (s1) minimalizovať.

Nech a je vektor celkových naakumulovaných denných pracovných časov vodičov za celé plánované obdobie rozpisovania služieb, potom prvok vektora ai spočítame ako:

$a_i = \sum_{j \in D} \sum_{T_k \in T} c_k x_{ijk}$ pre ∀V_i∈V

Nech L je celková dĺžka denných pracovných časov všetkých dostupných turnusov za celé obdobie rozpisovania služieb:

$L = \sum_{j \in D} \sum_{T_k \in T} c_k w_{jk}$

Nech H je celkové množstvo voľných pracovných síl v danom období:

$H = \sum_{V_i \in V} \sum_{j \in D} v_{jk}$

Nech $\overline a$ je ideálne priemerné trvanie turnusu na jednotku dňa:

$\overline a = \frac{L}{H}$

Je zrejmé, že najlepšia situácia ktorá môže nastať pri riešení DRP je, že každý vodič bude mať priemerný denný čas rovný hodnot $\overline a$ . Nech a^* predstavuje vektor ideálnych denných pracovných časov vodičov za celé plánované obdobie rozpisovania služieb.

$a_i^* = \overline a \sum_{j \in D} v_{ij}$ ,pre ∀V_i∈V

Podľa [11], [12] a [13] mieru nerovnomernosti f(a₁,…,a_m) definujeme na množine reálnych m-tíc (a₁,…,a_m) s nasledujúcimi vlastnosťami:

f(a₁,…,a_m) ≥ 0, a f(a₁,…,a_m) = 0 vtedy a len vtedy ak a₁ = ⋅⋅⋅ = a_m,
f je symetrická funkcia,
f(a₁ +d,…,a_m +d)=f(a₁,…,a_m) pre ľubovoľné reálne číslo d,
ak ∣x₁ −x₂∣ ≥ ∣a₁ −a₂∣ a x₁ +x₂ = a₁ +a₂ potom f(x₁,x₂,a₃,…,a_m) ≥ f(a₁,a₂,a₃ …,a_m),

Reálna funkcia f ∶ Rm → R kde (m > 2) je nazývaná Shur-konvexná, ak pre každú dvoj-stochastickú₂ maticu D máme f(Da) ≥ f(a) pre všetky a ∈ Rm. Jemnou úpravou mier nerovnomerností z [11], [12] a [13] získavame nasledujúce kritériálne funkcie:

$f_{dev}(a,a^*) = \sum_{V_i \in V} \vert \frac{a_i - a_i^*}{a_i^*} \vert$

(1)

$f_{ssqr}(a,a^*) = \sum_{V_i \in V} (a_i - a_i^*)^2$

(2)

V ďalšom texte sa stretneme s mierou nerovnomernosti (1) iba pri vyhodno- covaní výsledkov v závere článku³. Mieru nerovnomernosti (2) použijeme na určovanie rovnomernosti rozpisu služieb vodičov autobusov.

Príklad 3.1 (Zrovnomerňovanie pracovných výkonov vodičov)

Majme štyroch vodičov, ktorým sa snažíme priradiť tri turnusy, ktorých denné pracovné časy sú porade rovné hodnotám 1,3,7. Matica A predstavuje doteraz používaný štvordenný rozpis služieb s uvažovanými vodičmi a turnusmi. Prvkami matice sú uvažované pracovné časy turnusov. Nulový pracovný čas v matici znamená deň voľna pre daného vodiča. Uvažovaná matica má nasledovný tvar:

$A = \left( \begin{array}{cccc} 1 & 0 & 7 & 1 \\ 3 & 1 & 0 & 3 \\ 7 & 3 & 1 & 7 \\ 0 & 7 & 3 & 0 \end{array} \right)$

Pre takýto prípad získavame kumulované pracovné časy jednotlivých vodičov rovné hodnotám

$a=(9,7,18,10)$

Tieto kumulované pracovné časy v našom prípade predstavujú riadkové súčty matice A. Uvažujme prípad, kedy sú hodnoty parametrov v_ij = 1 pre ∀(V_i, j) ∈ V×D a w_jk =1pre∀(j,T_k)∈D×T. Z takéhoto predpokladu vyplýva,že vektor ideálnych kumulovaných pracovných časov i-teho vodiča je rovný hodnotám

$a^*=(11,11,11,11)$

Teraz môžeme spočítať mieru nerovnomernosti (2), ktorá je rovná hodnote

$f_{ssqr}(a,a^*) = 74$

Skúsme teraz vytvoriť viac rovnomerný rozpis služieb a dokážme, že tento nový rozpis služieb má menšiu mieru nerovnomernosti. Nech matica B predstavuje nový rozpis služieb. Stačí inak zoradiť prvky napríklad v štvrtý deň a získame nasledujúci rozpis služieb.

$B = \left( \begin{array}{cccc} 1 & 0 & 7 & 3 \\ 3 & 1 & 0 & 7 \\ 7 & 3 & 1 & 0 \\ 0 & 7 & 3 & 1 \end{array} \right)$

Vidíme, že hodnoty kumulovaných pracovných časov

$a=(11,11,11,11)$

sú rovné ideálnej priemernej hodnote. Z toho vyplýva, že miera nerovnomernosti (2) je rovné hodnote

$f_{ssqr}(a,a^*) = 0$

Aj keď v tomto prípade vieme intuitívne posúdiť, či je nový rozpis služieb B viac rovnomerný ako A, tak pri väčšom počte vodičov už potrebujeme poznať mieru nerovnomernosti.

Podobne je to aj s druhou ľahkou podmienkou. Tu sa snažíme maximalizovať frekvenciu rovnakých turnusov, ktoré majú byť priradené vodičom a zvýšiť tak ich skúsenosť na rovnakých alebo podobných trasách. Čím je miera nerovnomer- nosti väčšia, tým sú frekvencie rovnakých turnusov za celé obdobie rozpisovania služieb nerovnomernejšie. Z tohoto dôvodu sa snažíme mieru nerovnomernosti týkajúcu sa ľahkej podmienky (s2) maximalizovať.

Nech E = (e_il) je matica typu m_×t a nech jej prvky predstavujú celkovú naakumulovanú frekvenciu l-teho turnusu u i-teho vodiča za celé obdobie roz- pisovania služieb:

$e_{il} = \sum_{j \in D} x_{ijl}$ , pre ∀(V_i,T_l)∈V×T

Nech E_* = (e^*_il) je matica typu m_×t a nech jej prvky predstavujú ideálnu (ma- ximálnu) frekvenciu l-teho turnusu u i-teho vodiča za celé obdobie rozpisovania služieb.

$e_{il} = \sum_{j \in D} \sigma_{ijl}$ , pre ∀(V_i,T_l)∈V×T

Miera nerovnomernosti (2) určuje rovnomernosť prvkov vektora. Takéto ur- čovanie nám ale pri frekvenciách opakovania rovnakých turnusov už nestačí. Preto ich rozšírime na určovanie rovnomernosti prvkov v matici. Nech E = (e_il) je matica typu m_×t a nech E^* = (e^*_il) je matica typu m_×t, potom miery nerovnomernosti vzhľadom na prvky v matici E zapisujeme ako:

$f_{dev}(E,E^*) = \sum_{V_i \in V} \sum_{T_l \in T} \vert \frac{e_{il} - e_{il}^*}{e_{il}^*} \vert$

(3)

$f_{ssqr}(E,E^*) = \sum_{T_l \in T} (e_{il} - e_{il}^*)^2$

(4)

Príklad 3.2 (Maximalizácia frekvencie opakovania rovnakých turnusov)

Majme štyroch vodičov, ktorým sa snažíme priradiť tri turnusy. Matica C predstavuje doteraz používaný štvor-denný rozpis služieb nad uvažovanými vodičmi a turnusmi. Prvkami matice sú uvažované identifikačné čísla (id) turnusov. Nulové id v matici znamená deň voľna pre daného vodiča. Uvažovaná matica má nasledovný tvar:

$C = \left( \begin{array}{cccc} 1 & 0 & 3 & 2 \\ 2 & 1 & 0 & 3 \\ 3 & 2 & 1 & 0 \\ 0 & 3 & 2 & 1 \end{array} \right)$

V tomto prípade môžeme písať kumulovanú frekvenciu opakovania rovnakých turnusov ako maticu E:

$E = \left( \begin{array}{ccc} 1 & 1 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 1 \end{array} \right)$

Prvok matice E = (e_il) predstavuje hodnotu koľko-krát má priradený l-ty turnus i-ty vodič za obdobie štyroch dní. Vidíme, že sa žiadnemu vodičovi neopakuje žiaden turnus viacej krát ako raz. Ideálne by bolo, keby sa turnusy opakovali u vodičov čo najčastejšie⁴. Uvažujme prípad, kedy je parameter σ_ijl = 1 pre ∀(V_i,j,T_l) ∈ V ×D×T . Vzhľadom na predpoklad je ideálne opakovanie turnusov rovné hodnote počtu dní, t.j. e^*_il = 4 pre ∀(V_i,T_l) ∈ V×T . Teraz môžeme spočítať mieru nerovnomernosti (4) ktorá je rovná hodnote

$f_{ssqr}(E,E^*) = 108$

Skúsme vytvoriť viac znerovnomernený rozpis služieb vzhľadom na frekvenciu opakovania rovnakých turnusov a dokážme, že tento nový rozpis služieb má väčšiu mieru nerovnomernosti (4). Nech matica D predstavuje nový rozpis služieb. Stačí inak zoradiť prvky napríklad v štvrtý deň a získame nasledujúci rozpis služieb.

$D = \left( \begin{array}{cccc} 1 & 0 & 3 & 1 \\ 2 & 1 & 0 & 2 \\ 3 & 2 & 1 & 3 \\ 0 & 3 & 2 & 0 \end{array} \right)$

V tomto prípade môžeme písať frekvenciu opakovania rovnakých turnusov ako:

$E = \left( \begin{array}{ccc} 2 & 0 & 1 \\ 1 & 2 & 0 \\ 1 & 1 & 2 \\ 0 & 1 & 1 \end{array} \right)$

Z toho vyplýva, že miera nerovnomernosti (4) je rovné hodnote

$f_{ssqr}(E,E^*) = 114$

Druhá časť článku, ktorá výjde o týždeň formuluje riešenie problému prideľovania turnusov vodičom, teda popisuje podrobne druhý krok algoritmu deň-za-dňom. Sekcia sa skladá z problematiky definovania vstupných a výstupných hodnôt fuzzy inferenčného systému. Návrhu bázy dát a tvorby lineárneho matematického modelu.

¹ Text sa zaoberá prímestskou autobusovou dopravou, kde trasa spoja nepresahuje 50 km. Preto predpokladáme, že spoje sú časovo krátke a je výhodné z nich vytvárať turnusy.
²Nezáporná štvorcová matica sa nazýva dvoj stochastická, ak sa rovná každý jej súčet riadku a súčet stĺpca
³Výpočet a zobrazenie relatívnej odchýlky kumulovaného pracovného času od ideálneho za celé obdobie rozpisovania služieb
⁴Vzhľadom na zadanie je to ideálne, ale vzhľadom na skutočnosť prílišné opakovanie turnusov môže viesť k otupeniu vodičov.

O časopise

Meta

RSS

Implementácia heuristiky pre tvorbu rozvrhu služieb vodičov autobusov pomocou pyFuzzy I.

Napísať príspevok

Rubriky

Burza práce

Štúdijné materiály

Archív