Light source thermal analysis II – Incandescent Lamp
08. December, 2010, Autor článku: Fric Róbert, Elektrotechnika
Ročník 3, číslo 12  Pridať príspevok
Pridať príspevok
 The second chapter from the series of papers focused on thermal diagnostics of the light source deals with the heating of the regular incandescent lamp. The discussion about the possibilities of the accurate analysis of this simple device shows the difficulties and complexity of this thermal problem.
The second chapter from the series of papers focused on thermal diagnostics of the light source deals with the heating of the regular incandescent lamp. The discussion about the possibilities of the accurate analysis of this simple device shows the difficulties and complexity of this thermal problem.
1 Introduction
The heating problem of incandescent lamp is one of the most difficult cases for thermal analysis. It is due to its complicated convection inside and outside of the bulb. In this paper the specification of the regular incandescent lamp as a heat source has been made, and its heating evaluation has been showed analytically using the simplified equivalent thermal scheme. Also the surface temperatures of the incandescent lamp have been measured. The analytical results have been compared with measured values. The model has been described in the meaning of its relevancy and ability to use such a model in practice. It is appropriate to open the discussion about the methods of heating evaluation of this kind of systems.
2 Heat source specification
The radiation spectrum of the incandescent light source is continuous and smooth (Fig. 1); therefore the specification of the quantity of generated heat can also be determined using radiation theory of the black body. The power balance must comply with such an enumeration.
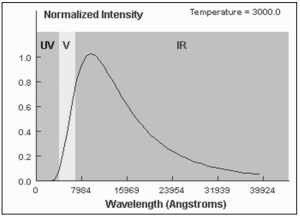
Fig. 1 Spectral density of black body radiation at 3000K, [8]
We determine the value of the heat flux of the light bulb from the power balance of the light source [3]. Normal light bulb represents incandescent heat (and light) source. The wolfram wire heated to 2800 °C emits the light and the heat. But the most of the energy flows out as a heat.
Numerically, the heat is taken out in form of IR radiation (about 83%) and also by conduction and convection out of the bulb (about 12%). So the heat generated by the filament is about 95% of the lamp power (Fig. 2). The small amount of UV radiation has been omitted.
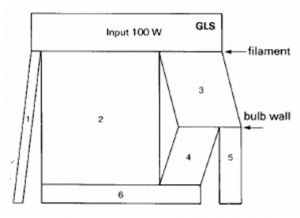
Fig. 2 Energy balance of the regular incandescent lamp [3]
- Visible light: 5%
- IR radiation from filament: 61%
- Convection and conduction from filament to bulb: 34%
- IR radiation from bulb: 22%
- Convection and conduction from bulb to environment: 12%
- Sum of IR radiation to environment: 83%
3 Analytical calculation of the heating
First we have to take a look at the structure of the light bulb and eventually apply some simplifications. We will think of filament as a small sphere with equivalent surface. It is because the double-wound filament is too complex to modeling or analytic calculation. We will consider the gas filling of the bulb as a medium with the same thermal conductivity as the air. In real, the filling is the Argon and Nitrogen atmosphere and convection is not isotropic. Over that, we will model the bulb as the sphere without the cap.
We used the system of co-centric spheres (Fig. 3) as a model. A cross-section of them represents the cutting of the lamp locally in the filament zone. The inner cylinder represents the filament; the outer cylinder represents the glass bulb of the lamp. Between these faces there is a gas filling.
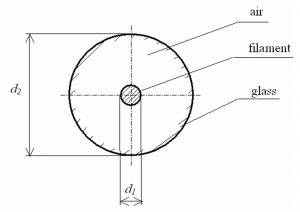
Fig. 3 Geometrical model of the incandescent lamp.
d1: diameter of filament equivalent sphere, d2: diameter of the bulb sphere
Next we arrange the equivalent thermal diagram and solve it as an electric circuit – as used also in [1]. The equivalent thermal diagram of the incandescent lamp is shown in Fig. 4. We need to calculate the values of filament temperature t1 and bulb temperature t2. We assume that:
- There is convection and radiation between light bulb and space and between the filament and the bulb and also between filament and space
- The gas inside the bulb has the same thermal conductivity as the air
- The filament is modeled as the small sphere
- The light bulb glass is very thin
- There is no heat conduction between filament and bulb (long filament support)
The source of the heat has been set as a heat flux P (in Watts) to node t1. The same heat flux will be taken out from node t0.
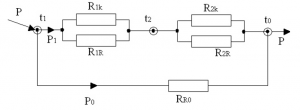
Fig. 4 Equivalent thermal diagram
The calculation of the temperatures has been done by solving the system of equations:
| (1) |
| (2) |
Where: R is total heat resistance, R2 is the heat resistance between bulb and environment (space), convection and radiation, P is the filament generated heat flux, P1 is the heat flux between filament and glass bulb as an equivalent convection, P0 is the radiation heat flux from the filament directly to space through heat resistance, t0, t1, t2 are temperatures of the environment, filament and bulb.
The heat resistances evaluation is made according to [2] and it is similar to previous paper. The equivalent thermal diagram is solvable as an electrical circuit, considering the equivalency of the temperature and electric fields [1], [4]. The solution consists of solving the non-linear system of equations with the unknown temperatures. Heat resistances Rik (convection) and RiR (radiation) depend on the surface temperatures, so that iterative evaluation of the final surface temperatures must be used.
Again, it is necessary to use the computer system to evaluate the results. Temperatures of this solution were evaluated by using software Mathematica [7]. In each iteration cycle we evaluated also the coefficient of the heat transfer from the surface and equivalent thermal conduction coefficient
, both solved through criterion equations for sphere geometry, ref. [1], [4].
We assumed the input values for the model: space temperature t0 = 20°C, power of the lamp Pw = 60 W, heat generated inside the model P = 57 W, filament emissivity = 0.27, bulb glass emissivity
= 0.95. We also use the temperature functions of Pr ,
a
evaluated for dry air as a filling of the bulb [5]. The results of the analytical calculation of the temperatures are shown in Tab. 1.
Tab.1 The results of the calculation of the model
| Filament temperature | t1 = 2894 [°C] |
|---|---|
| Bulb temperature | t2 = 159 [°C] |
| Gas equivalent conductance | |
| Heat transfer coefficient | |
| Thermal flux through P0 | P0 = 26.1 [W] |
| Thermal flux through P1 | P1 = 30.9 [W] |
4 Experiment – measurement of the temperatures
The heating of the OSRAM 60W incandescent lamp was measured by the NiCr thermocouples attached to bulb surface (Fig. 5). Measurement was performed by the same conditions, as analysis assumed – the lamp was placed free in the air. The lamp was measured at the two operating positions noticing the influence of the inner bulb convection.
The measurement was dynamic and ran at least 20 min to obtain the steady state. The settled temperatures for each of measurement points are displayed also in the Fig. 5, where we can see the change of temperatures according to its operating position. The space temperature was about 20°C.
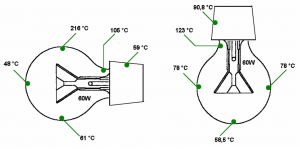
Fig. 5 Temperatures of the 60W lamp
5 Conclusion
The real temperature of the filament is about 2700°C and slightly changes with the input power. The temperature obtained from our simple thermo-mechanic model is approx. 2894°C, which corresponds with the real values.
It is now clear, that the bulb temperatures are much related with operating position. For comparison with the calculation we can only estimate, that the average value can range between 100°C and 200°C. The average bulb temperature of the analytical model is 159°C. We are not able to obtain more accurate results from this model, because of its large simplifications. We also cannot set up more complex analytical model of the real light bulb because of its thermal characteristics.
The heat transfer inside the light bulb is very non-uniform in real, so it is very hard to describe the heat transfer by static explicit model. The solution of this problem is to use the computer finite-element method with modeling of the fluid fields (Finite Element Method, Computational Fluid Dynamics). We are able to get usable results of the static model for simple problems at the moment – for example in the design process of the particular elements. The analytical calculations also provide evaluation of input values for numerical analysis of the problem by finite element method, which is also usable. But here is a request to use a more exact convection model for this type of problem in the future.
References
- Janíček, F. – Murín, J. – Lelák, J.: Load Conditions and Evaluation of the Rise of Temperature in an Enclosed Conductor. Journal of Electrical Engineering, 52 (7-8), 2001, p. 210-215.
- Michejev, M.A. – Michejeva, I.M: Osnovy teploperedači. Energia, Moskva, 1977.
- Philips Lighting: Lighting manual – Fifth Edition. Philips Lighting B.V. Eindhoven 1993.
- Kalousek, M. – Hučko, B.: Prenos tepla. Bratislava: Vydavateľstvo STU, 1996
- Ražnjevič, K. Tepelné tabuľky a diagramy. ALFA, Bratislava 1969.
- http://www.wolfram.com
- http://csep10.phys.utk.edu
Department of Mechanics, Faculty of Electrical Engineering and Information Technology, Ilkovičova 3, 812 19 Bratislava 1, Slovak University of Technology in Bratislava


11. November, 2011 o 15:26
I read your excellent paper on the thernal analysis of conventional incandescent lamps. have you perhaps done similar work on linear tungsten halogen incandescent lamps?
11. November, 2011 o 15:27
I read your excellent paper on the thermal analysis of conventional incandescent lamps. have you perhaps done similar work on linear tungsten halogen incandescent lamps?
12. September, 2012 o 13:48
Hello, thank you for your suggestion. The thermal field profile of the linear version of lamp will be very similar in cross-section, but I didn’t worked on that yet. The solution method can be as like as for the Sodium High-pressure Discharge Lamp described in http://www.posterus.sk/?p=9314 but including thermal convection inside the lamp. So the results I expect can be closer to Incandescent lamp because of non-uniformity of that thermal problem. Let’s work on it