Mechanical vibration, Chapter 2: Free vibration of undamped 1-DOF linear system, Part 2: Dynamics of vibration

02. Január, 2013, Autor článku: Goga Vladimír, Elektrotechnika
Ročník 6, číslo 1 This page as PDF Pridať príspevok

In this part the free vibration of undamped 1-DOF linear system is solved from the dynamics point of view. We will deal with the forces that affect the vibratory motion of the oscillator. Dynamics analysis of vibration oscillator leads to the differential equation of motion which will be solved.

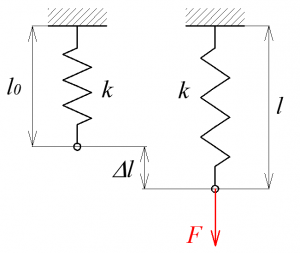
Undamped 1-DOF mass-spring oscillator is characterized by mass weight m and spring stiffness k. Everybody knows what the mass weight is. But what is spring stiffness? Spring represents elastic discrete 1-DOF element with no mass. Spring is characterized by stiffness coefficient k. This coefficient is a measure of the resistance offered by an elastic body to deformation (Fig. 1):

k=\frac{F}{\Delta l}


Fig. 1 Spring deformation.

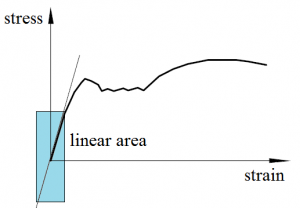
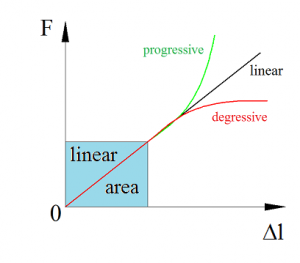
where F is the force applied on the body and Δl is the displacement produced by the force along the same DOF (the change in length of a stretched spring). Physical unit for spring stiffness is newton/meter [N/m]. Mentioned equation is correct just for springs with linear characteristic (linear relationship between force and deformation). Mechanical properties of materials are nonlinear in general, but deformations of real springs and construction materials are usually small, where their force-deformation dependencies are linear (Fig. 2).


(a)


(b)
Fig. 2 Linear area of mechanical properties: material stress-strain diagram (a), spring characteristics (b).

Mass equilibrium position determined by spring deformation due to gravitational force FG of the mass m. This position is conditioned by equilibrium of spring static force Fst and mass gravitational force FG (Fig. 3). This spring deformation is called static deformation yst. From definition of spring stiffness we can calculate spring static deformation:

F_G=m.g, \; F_{st}=k.y_{st}
F_G=F_{st} \Rightarrow m.g=k.y_{st}
y_{st} = \frac{F_G}{k} = \frac{m.g}{k}

where g is Earth’s gravity. Mass starts vibrate when is displaced from equilibrium position, therefore the mass gravity is not considered further.


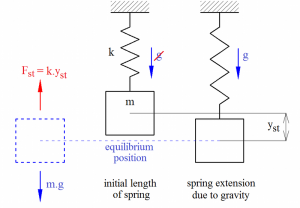
Fig. 3 Static deformation of spring.

During free vibration two forces act on the mass (Fig. 4): spring force Fk and mass inertia force Fm. Value of spring force is determined by displacement mass from equilibrium position:

F_k = k.y

where y is mass displacement. Value of inertia force is determined by acceleration of mass:

F_m = m.a

where a is mass acceleration.




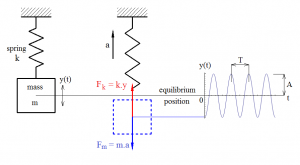
Fig. 4 Forces act on the mass.

Forces Fm and Fk act opposite to each other:

F_m=-F_{k} \Rightarrow m.a=-k.y
m.a+k.y=0 \Rightarrow m.\ddot{y}+k.y=0

The final equation is 2nd order homogeneous differential equation of free vibration motion undamped 1-DOF linear system. From kinematics of vibration we know:

y=A.sin(\omega t) and \ddot{y}=-\omega^2.A.sin(\omega t)

and then

m.\ddot{y}+k.y = 0 \Rightarrow
-m.\omega^2.A.sin(\omega t)+k.A.sin(\omega t)=0 \Rightarrow
-m.\omega^2+k=0
\omega=\omega_0=\sqrt{\frac{k}{m}}

This is angular frequency ω of free vibration and is called natural angular frequency ω0. Every vibrating system has one or more natural angular frequencies that it will vibrate at once it is disturbed. Number of natural frequencies is equal to number of DOF (continuum system has theoretically infinity number of natural frequencies). Natural angular frequency ω0 is dependent on stiffness k and mass m of the system.Equation of free vibration motion for our undamped 1-DOF linear system can be rewrite:

\ddot{y} + \omega_0^2 y=0

This equation of motion describes general vibration motion but every system can be forced by different initial displacement or velocity. These initial conditions must be applying to the equation of motion. Let’s consider a vibration system synchronously forced by initial displacement y0 and initial velocity v0 (in time: t0 = 0 s). Displacement-time diagram produced by initial displacement is shown in Fig. 5 and is describe by cosine function:

y_1=B.cos(\omega_0 t)

where B is amplitude of displacement.


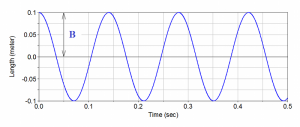
Fig. 5 Displacement-time diagram: y1=B.cos(ω0.t).

Displacement-time diagram produced by initial velocity is shown in Fig. 6 and is describe by sine function:

y_2=A.sin(\omega_0 t)

where A is amplitude of displacement.


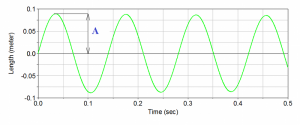
Fig. 6 Displacement-time diagram: y2=A.sin(ω0.t).

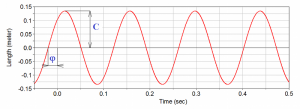
Final displacement y is then sum of y1 and y2(Fig. 7):

y=A.sin(\omega_0 t)+B.cos(\omega_0 t)

Amplitudes A and B are determined from initial conditions for t0 = 0 s:

y_0=A.sin(\omega_0.0)+B.cos(\omega_0.0) \Rightarrow B=y_0
v_0=\dot{y}_0=\omega_0.A.cos(\omega_0.0)-\omega_0.B.sin(\omega_0. 0) \Rightarrow A=\frac{\dot{y}_0}{\omega_0}

Final displacement is then expressed:

y=\frac{\dot{y}_0}{\omega_0}sin(\omega_0.t) + y_0.cos(\omega_0.t)

This solution can be replaced by sine function:

y=C.sin(\omega_0.t+\varphi)

where amplitude C and phase angle ϕ are:

C=\sqrt{\left ( \frac{\dot{y}_0}{\omega_0} \right )^2+(y_0)^2}
\varphi = arctan\frac{y_0 \omega_0}{\dot{y}_0}


Fig. 7 Final displacement-time diagram: y=C sin(ω0.t+φ).

Napísať príspevok