Prehľad metód porovnania fuzzy čísel

20. Júl, 2011, Autor článku: Ladovský Tomáš, Informačné technológie
Ročník 4, číslo 7 Pridať príspevok

Článok sa venuje problematike porovnania neistých údajov, ktoré modelujeme fuzzy trojuholníkovými číslami. V dnešnej dobe existuje veľké množstvo metód, ktoré porovnávajú fuzzy čísla rôznymi prístupmi. Jedným takýmto prístupom je porovnanie fuzzy čísel vzhľadom na informáciu vyplývajúcu z ich ťažísk. Taktiež lexikografický a agregačný prístup vedie k pozitívnym výsledkom. Cieľom článku je experimentálne porovnať ich neúspešnosť s akou usporiadavajú fuzzy čísla. Pod pojmom neúspešnosť si môžeme predstaviť počet rôznych fuzzy čísel, ktoré daná metóda považuje za totožné.

1. Úvod

Pojem fuzzy množiny bol prvý krát predstavený americkým expertom na automatizáciu L. A. Zadehom [9] a pojem fuzzy čísla predstavili Jain [2] a Dubois a Prade [1]. Výskum porovnania fuzzy čísel je jednou z veľmi dôležitých tém teórie fuzzy množín a aplikuje sa na všetky oblasti rozhodovania. Napríklad poňatie optimality alebo výberu najlepšieho riešenia je kompletne založené na porovnaní (poradí). Fuzzy čísla nevieme ľahko usporiadať v poradí ich veľkosti, pretože predstavujú neisté a neurčité hodnoty, ktoré vyjadrujeme možnostnými rozdeleniami a môžu sa navzájom prekrývať. Ak sa dve fuzzy čísla prekrývajú, potom ich nemožno považovať za absolútne usporiadateľné [3].

To znamená, že jedenkrát môžeme považovať fuzzy číslo za väčšie ako ostatné, no pri inom porovnaní ho môžeme považovať za menšie ako ostatné. Ak usporiadame fuzzy čísla z obrázka 1(a) podľa ťažiska, Yagerov index [8], tak získame výstupnú postupnosť A₂, A₁, A₃, A₄, kde A₂ je najmenšie a A₄ najväčšie fuzzy číslo. U fuzzy čísel A₂ a A₄ je ihneď jasné, že fuzzy číslo A₄ je absolútne väčšie ako A₂. Ak sa ale fuzzy čísla navzájom prekrývajú, potom ich nemôžeme považovať za absolútne usporiadateľné. Napríklad, fuzzy čísla A₁ a A₃ sa navzájom prekrývajú a tak nemôžeme považovať fuzzy číslo A₃ za absolútne väčšie ako A₁. Stále totiž existuje možnosť, že A₁ je väčšie ako A₃.

Na porovnanie fuzzy hodnôt neexistuje univerzálna metóda, tak ako sme zvyknutí u reálnych čísel. V dnešnej dobe existuje veľké množstvo metód, pomocou ktorých sme schopní porovnať fuzzy čísla. Rozdielne prístupy porovnania fuzzy čísel môžeme podľa Nasseriho [5] a Ramliho [6] kategorizovať do štyroch hlavných tried: I. relácie preferencie: a) stupeň optimality, b) Hamingová vzdialenosť, c) alfa-rez, d) porovnávacia funkcia; II. posibilitné (posibilita – možnosť) rozdelenia fuzzy priemeru a rozptylu; III. fuzzy bodovanie: a) prispôsobenie sa k optimu, b) ľavé a pravé bodovanie, c) index ťažiska, d) plošné merania; IV. lingvistické vyjadrovanie: a) intuícia, b) lingvistická aproximácia. My k tejto skupine pridáme lexikografické a agregačné metódy a taktiež sa pozrieme na niekoľko centroidných metód. Nasledujúca sekcia definuje pojmy ako fuzzy množina, nosič fuzzy čísla, výška fuzzy čísla, normálne číslo, fuzzy číslo a alfa rez fuzzy čísla.

2. Fuzzy čísla

Nech $\mathfrak R$ je množina reálnych čísel. Fuzzy množinu A definujeme na $\mathfrak R$ pomocou funkcie príslušnosti $\mu_A:\mathfrak R\rightarrow [0,1]$ , kde $\mu_A(x)$ predstavuje stupeň príslušnosti elementu x vo fuzzy množine A. Fuzzy podmnožina A definovaná na $\mathfrak R$ je normálna, ak a iba ak

$H(A) = \sup_{x\in \mathfrak R}\{\mu_A(x)\} = 1$

kde H(A) je výška fuzzy množiny A. Fuzzy podmnožina $A$ množiny $\mathfrak R$ je konvexná, ak a iba ak $\mu_A(\lambda x+(1-\lambda)y)\geq\min\{\mu_A(x),\mu_A(y)\},$ kde $x,y\in\mathfrak R$ a $\lambda\in [0,1]$ . Nosič množiny A je definovaný ako $S(A) = \{x\,|\, \mu_A(x) > 0\}.$ Fuzzy množinu A sa nazýva fuzzy číslo, ak a iba ak A je normálna, konvexná a nosič množiny A je ohraničený na $\mathfrak R$ . Trojuholníkové fuzzy číslo A je fuzzy číslom so spojitou lineárnou funkciou príslušnosti $\mu_A(x)$ definovanou ako:

$\mu_A(x) = \left\{ \begin{array}{ccc} \mathcal L_A(x) = (x-a)/(b-a) & \text{pre} & a\leq x\leq b, \\ \mathcal R_A(x) = (c-x)/(c-b) & \text{pre} & b\leq x\leq c, \\ 0 &\text{inak},& \end{array} \right .$

(1)

kde $\mathcal L_A:[a,b]\rightarrow [0,1]$ je striktne rastúca funkcia a $\mathcal R_A:[b,c]\rightarrow [0,1]$ je striktne klesajúca funkcia. V nasledujúcom texte používame namiesto pojmu trojuholníkové fuzzy číslo skrátený tvar fuzzy číslo. Fuzzy číslo môžeme taktiež značiť ako usporiadanú trojicu $A = (a,b,c)$ , kde $a\leq b\leq c$ a $a,b,c\in\mathfrak R$ . Hodnota a je nazývaná infimom, b je nazývaná modusom a c je nazývaná suprémom. Taktiež sa používajú označenia pre a ako ľavá hodnota, spodná hodnota, pre b sa používajú označenia ako centrálna hodnota, stredná hodnota a pre c sa používajú označenia ako pravá hodnota, horná hodnota.

V nasledujúcom texte sa obmedzíme na také trojuholníkové fuzzy čísla, ktorých hodnoty usporiadanej trojice sa nerovnajú. Definujme množinu všetkých fuzzy čísel s reálnymi hodnotami a,b,c ako $\mathcal N(\mathfrak R) = \{(a,b,c)\,|\,a < b < c,\, a,b,c\in\mathfrak R\}.[/latex] A nech $\mathcal N(N) = \{(a,b,c)\,|\,a < b < c,\, a,b,c\in N_0\}$ je množina všetkých fuzzy čísel s prirodzenými hodnotami a,b,c. Inverzné funkcie [latex]\mathcal L^{-1}_A:[0,1]\rightarrow [a,b][/latex] a [latex]\mathcal R^{-1}_A:[0,1]\rightarrow [b,c][/latex] k funkciám [latex]\mathcal L_A[/latex] a [latex]\mathcal R_A[/latex] definujeme (viď. obrázok 1(b)) pre fuzzy číslo A ako [latex]\mathcal L^{-1}_A(y) = a+(b-a)y[/latex] a [latex]\mathcal R^{-1}_A(y) = c + (b - c)y[/latex], kde [latex]y\in[0,1][/latex]. <a href="http://www.posterus.sk/wp-content/uploads/p11018_01_obr01a.png"><img src="http://www.posterus.sk/wp-content/uploads/p11018_01_obr01a-300x190.png" alt="" title="p11018_01_obr01a" width="300" height="190" class="alignright size-medium wp-image-11031" /></a> (a) Problém porovnania fuzzy čísel <a href="http://www.posterus.sk/wp-content/uploads/p11018_02_obr01b.png"><img src="http://www.posterus.sk/wp-content/uploads/p11018_02_obr01b-300x209.png" alt="" title="p11018_02_obr01b" width="300" height="209" class="alignright size-medium wp-image-11032" /></a> (b) Ukážka inverznej funkcie členstva fuzzy trojuholníkového čísla A=(0,0.5,1) Fig. 1 Na ľavom obrázku (a) sú zobrazené štyri fuzzy čísla, na ktorých demonštrujeme problém ich porovnania. Fuzzy čísla A2 a A3 sa s fuzzy číslom A4 neprekrývajú, preto vieme ľahko povedať, že A2 a A3 sú menšie ako A4. Ako je to ale s fuzzy číslami A1 a A3. Tieto dve fuzzy čísla sa prekrývajú. Pre <img src='http://s0.wp.com/latex.php?latex&bg=ffffff&fg=000000&s=0' alt='' title='' class='latex' />\alpha$ -rezy oboch fuzzy čísel platí, že ${A_3}_\alpha$ je podmnožinou ${A_1}_\alpha$ , pre $\alpha\in[0,0.23)$ . To znamená, že pri pesimistickej optimalizácií, kde preferujeme väčšiu šírku intervalu ${A_1}_\alpha$ pred menšou ${A_3}_\alpha$ , zvolíme za väčšie fuzzy číslo A₁ a to pre hladiny $\alpha\in[0,0.23)$ . Pre hladiny $\alpha\in[0.23, 0.6)$ nastáva nejasná situácia, ktorý $\alpha$ -rez je väčší a ktorý menší, aj keď pravá hodnota intervalu ${A_3}_\alpha$ je väčší ako pravá hodnota intervalu ${A_1}_\alpha$ . Nakoniec pre hladiny $\alpha\in[0.6, 1]$ sa intervaly ${A_1}_\alpha$ a ${A_3}_\alpha$ neprekrývajú. Alfa rez ${A_3}_\alpha$ je väčší ako ${A_1}_\alpha$ , a to z toho dôvodu, že ľavá hodnota ${A_3}_\alpha$ je väčšia ako pravá hodnota ${A_1}_\alpha$ . Na pravom obrázku (b) je zobrazená inverzná funkcia členstva fuzzy trojuholníkového fuzzy čísla.

Označme reálny interval $A_\alpha$ ako $\alpha$ -rez fuzzy množiny A a definujme ho ako

$A_\alpha = [a^L_\alpha,a^R_\alpha] = [\mathcal L^{-1}_A(\alpha), \mathcal R^{-1}_A(\alpha)] =[a+(b-a)\alpha,c+(b-c)\alpha]$

Nech $m(A_\alpha)$ je centrálna hodnota elementov $\alpha$ -rezu, ktorú pre fuzzy číslo $A = (a,b,c)$ spočítame ako $m(A_\alpha) = m[a^L_\alpha,a^R_\alpha] = ((2b-a-c)\alpha + (a+c))/2,$ kde $\alpha\in[0,1]$ . Nech A je ľubovoľné fuzzy číslo A = (a,b,c), potom obsah plochy a(A) pod grafom $m(A_\alpha)$ (viď. obrázok 2(a)) spočítame pre $\alpha\in[0,1]$ ako $a(A) = \int_0^1 m[a^L_\alpha,a^R_\alpha]\,d\alpha = (a+2b+c)/4.$

Strednú hodnotu fuzzy čísla A spočítame ako $m(A) = (a+b+c)/3$ a smerodajnú odchýlku fuzzy čísla A spočítame ako $s(A) = \sqrt{a^2+b^2+c^2-ab-bc-ac}/(3\sqrt{2}).$ Ukážku strednej hodnoty a smerodajnej odchýlky fuzzy čísla A môžeme vidieť na obrázku 2(b).

(a) Ukážka obsahu ohraničeného funkciou $m(A_\alpha)$ a x-ovou osou

(b) Ukážka strednej hodnoty a smerodajnej odchýlky fuzzy čísla A
Fig. 2 Na ľavom obrázku (a) môžeme vidieť obsah oblasti ohraničenej funkciou $m(A_\alpha)$ a x-ovou osou. Pravý obrázok (b) zobrazuje strednú hodnotu a smerodajnú odchýlku fuzzy čísla A

Nasledujúca sekcia definuje niekoľko metód porovnania fuzzy trojuholníkových čísel.

3. Metódy porovnania fuzzy čísel

Nech $\mathcal N(\mathfrak R)$ je množina všetkých fuzzy čísel definovaných na množine reálnych čísel $\mathfrak R$ a $A,B\in\mathcal N(\mathfrak R)$ . Nasledujúci text porovnáva fuzzy čísla pomocou funkcie $F: \mathcal N(\mathfrak R)\rightarrow\mathfrak R$ , ktorú nazývame porovnávacia funkcia alebo index porovnania (angl. ranking function, ranking index). Ak platí $F(A)\leq F(B)$ , potom $A\leq B$ a znamená to, že fuzzy číslo A je menšie alebo rovné ako B vzhľadom na zvolenú funkciu porovnania.

Výsledky optimalizačného problému sú závislé na správnej voľbe funkcie porovnania a to vzhľadom na preferenciu riešiteľa, ktoré môžu byť známe pred začatím procesu optimalizácie (apriórne techniky), v priebehu procesu optimalizácie (interaktívne techniky) alebo až po skončení optimalizácie (aposteriórne techniky). Medzi apriórne techniky patrí lexikografický a agregačný prístup. Yager v roku 1980 [8] navrhol, že väčšie z dvoch fuzzy čísel je to, ktoré má väčšiu hodnotu

$F^{(1)}(A) = m(A)$

Na Yagerov index sa ešte pozrieme detailnejšie neskôr a to z toho dôvodu, že sa tento index stal základom novej vetvy metód porovnania fuzzy čísel (centroidné metódy). Väčšie fuzzy číslo má väčšiu hodnotu $F^{(1)}(A)$ . Bector a Chandra použili na porovnanie dvoch fuzzy čísel funkciu porovnania

$F^{(2)}(A) = a(A)$

Väčšie fuzzy číslo má väčšiu hodnotu $F^{(2)}(A)$ .

Ak porovnávame fuzzy čísla iba na základe jednej hodnoty (porovnávacia funkcia, index), tak potom dochádza k určitej strate informácie alebo index porovnania považuje veľkú množinu rôznych fuzzy čísel za rovnaké. Preto sa používajú multikriteriálne optimalizačné techniky ako lexikografický prístup a agregačný prístup. V lexikografickom prístupe sa rozhoduje podľa viacerých kritérií. McCahon a Lee [4] stanovili dve kritéria

$F^{(3)}_1(A) = m(A),\quad\text{a}\quad F^{(3)}_2(A) = s(A).$

Väčšie z dvoch fuzzy čísiel je to, ktoré má väčšiu strednú hodnotu $F^{(3)}_1$ , v prípade zhody stredných hodnôt je väčšie to s väčšou smerodajnou odchýlkou $F^{(3)}_2$ . Sakawa a Kubota [7] použili pre porovnanie fuzzy čísiel A = (a,b,c) tri kritéria.

$F^{(4)}_1(A) = a(A),\quad\text{a}\quad F^{(4)}_2(A) = b,\quad\text{a}\quad F^{(4)}_3(A) = c - a.$

Väčšie z dvoch fuzzy čísiel je to, ktoré má väčšiu hodnotu $F^{(4)}_1$ , v prípade zhody hodnôt $F^{(4)}_1$ je väčšie to s väčšou modálnou hodnotou $F^{(4)}_2$ a v prípade zhody hodnôt $F^{(4)}_2$ je väčšie to s väčším nosičom $F^{(4)}_3$ .

Nedostatkom lexikografického prístupu je dominancia prvého kritéria. Napríklad, A a B sú fuzzy čísla a platí $m(B) = m(A)+\epsilon$ , kde $\epsilon$ je malé kladné číslo a $s(B)<<s(A)[/latex], potom fuzzy číslo A je podľa McCahonho kritéria vyhodnotené ako menšie než B. Tento nedostatok môžeme odstrániť agregačným prístupom, ktorým skladáme z viacerých dielčich kritérií celkové kritérium a to na základe sčítania dielčich kritérií s použitím nezáporných váhových koeficientov [latex]w = (w_1,w_2,w_3,\dots)\geq 0[/latex]. Na základe McCahonho kritéria môžeme napríklad navrhnúť kritérium kombinujúce strednú hodnotu a smerodajnú odchýlku ako <table style="width:100%;"> <tr> <td style="text-align:center;"><img src='http://s0.wp.com/latex.php?latex&bg=ffffff&fg=000000&s=0' alt='' title='' class='latex' />F^{(5)}(A) = w_1m(A) + w_2s(A), \text{ kde } w_1,w_2\geq 0$

Iný spôsob porovnania fuzzy čísel je založený na vypočítaní súradníc ťažiska $T = (\hat{x},\hat{y})$ a porovnaní fuzzy čísel vzhľadom na hodnoty $\hat{x}, \hat{y}$ alebo vzdialenosti ťažísk T od počiatku súradnicovej sústavy (0,0). Taktiež existujú rôzne modifikácie tejto metódy, ktorá sa označuje ako metóda porovnania indexov ťažiska alebo jednoducho ako centroidné metódy porovnania fuzzy čísel (angl. centroid index ranking methods).

Ako prvý prispel do metód porovnania fuzzy čísel s pojmom index ťažiska Yager v roku 1980 [8]. Vypočítal horizontálnu pozíciu ťažiska $\hat{x}_A$ fuzzy čísla A a túto hodnotu použil ako index porovnania. Túto hodnotu spočítame ako

$\hat{x}_A = \frac{\int_{x}w(x)\mu_A(x)\,dx}{\int_{x}\mu_A(x)\,dx}$

kde w(x) predstavuje funkciu váh významu hodnoty x. Pre w(x)=x sa horizontálna súradnica ťažiska $T(A) = (\hat{x}_A,0)$ stáva ťažiskom (COG). Čím je index $\hat{x}_A$ väčší, tým je fuzzy číslo A hodnotené ako väčšie. Pre w(x)=x definujeme Yagerov index ako

$F^{(1)}(A) = \hat{x}_A = m(A)$

Murakami a kol. v roku 1983 prezentovali horizontálne a vertikálne súradnice bodu ťažiska. Horizontálna súradnica $\hat{x}_A$ je rovnaká ako pri Yagerovi. Čím je index $\hat{x}_A$ a/alebo $\hat{y}_A$ väčší, tým je fuzzy číslo A väčšie. Podľa Bortolan a Degani (1985) je logická iba voľba horizontálnej súradnice, pretože vertikálna hodnota je rovnaká pre všetky normálne trojuholníkové fuzzy čísla $(\hat{y}=1/3)$ . Teda podľa Murakamiovho indexu sa na súradnicu $\hat{x}$ pozeráme ako na hlavný index a na súradnicu $\hat{y}$ pozeráme ako na pomocný index. Cheng v roku 1998 navrhol index vzdialenosti, ktorý je založený na oboch súradniciach ťažiska a môžeme ho definovať ako

$F^{(6)}(A) = \sqrt{{\hat{x}_A}^2 + {\hat{y}_A}^2}$

Horizontálna súradnica $\hat{x}_A$ je totožná s Yagerom a Murakamiom a pre fuzzy číslo A = (a,b,c) je vertikálna súradnica $\hat{y}_A$ rovná

$\hat{y}_A = \frac{(a+4b+c)}{3(a+2b+c)}$

Pôvodná Chengova metóda je špecializovaná pre porovnanie lichobežníkových fuzzy čísel, ale môže byť taktiež aplikovaná na všeobecné fuzzy čísla, pokiaľ je ľavá a pravá funkcia príslušnosti invertabilná. Nevýhodou metódy je, že nevie porovnávať negatívne fuzzy čísla. Chu a Tsao navrhol v roku 2002 ako index porovnania plochu medzi bodom ťažiska $T_A = (\hat{x}_A,\hat{y}_A)$ a stredom súradnicovej sústavy (0,0), ktorú definoval ako

$F^{(7)}(A) = \hat{x}_A\hat{y}_A$

kde $\hat{x}_A$ a $\hat{y}_A$ je totožné s Chengom. Väčšia plocha reprezentuje väčšie fuzzy číslo. Chen a Chen v roku 2003 zistili, že Chengová (1998), Murakamiová a kol. (1983) a Yagerová (1980) metóda nevie v určitých situáciách porovnať rozdielne fuzzy čísla (viď. obrázky 3) a taktiež nevedia spočítať poradie pre ostré hodnoty. Z tohoto dôvodu Chen a Chen odvodili novú metódu, založenú na súradniciach ťažiska $T=(\hat{x},\hat{y})$ a smerodajnej odchýlke s(A). Chen a Chenov index porovnania pre fuzzy čísla A=(a,b,c) je definované ako

$F^{(8)}(A) = \hat{x}_A + (1-\hat{y}_A)^{s(A)}$

kde horizontálna súradnica je rovná hodnote

$\hat{x}_A=(2b\hat{y}_A+(c+a)(1-\hat{y}_A))/2$

a vertikálna súradnica je buď rovná hodnote $\hat{y}_A = 1/3$ ak $a\neq c$ alebo $\hat{y}_A = 1/2$ ak a=c. Čím je hodnota $F^{(8)}(A)$ väčšia, tým je fuzzy číslo väčšie. Pôvodná Chen a Chenová metóda je špecializovaná pre porovnanie zovšeobecnených lichobežníkových fuzzy čísel. Nasledujúca sekcia skúma klady a zápory vlastností metód porovnania fuzzy čísel.

4. Vlastnosti metód porovnania fuzzy čísel

Yagerov index $F^{(1)}$ je jeden z prvých a najjednoduchších indexov porovnania fuzzy čísel a jeho myšlienku môžeme nájsť v ďalších indexoch porovnania, ktoré vychádzajú z ťažiska fuzzy čísla (strednej hodnoty fuzzy čísla). Geometricky, zodpovedá stredná hodnota ťažisku diagramu posibilného rozdelenia. Na obrázku 3(a) je zobrazený spôsob akým Yagerov index porovnáva dve fuzzy čísla. Na ďalšom obrázku 3(b) môžeme vidieť jednu z mnohých situácií, kedy index nedokáže určiť z dvoch fuzzy čísel to väčšie.

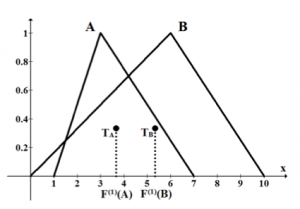
(a) Porovnanie fuzzy čísel pomocou Yagerovho indexu, fuzzy číslo A je vyhodnotené ako menšie ako B

(b) Fuzzy čísla pre ktoré nevieme určiť poradie, fuzzy čísla A, B sú vyhodnotené ako rovnaké

(c) Fuzzy čísla pre ktoré nevieme určiť poradie

(d) Fuzzy čísla pre ktoré nevieme určiť poradie
Fig. 3 Ukážka použitia Yagerovho indexu na porovnanie dvoch fuzzy čísel, kde na obrázku (a) vidíme, že horizontálna súradnica ťažiska fuzzy čísla A je menšia ako horizontálna súradnica ťažiska fuzzy čísla B, t.j. $F^{(1)}(A) < F^{(1)}(B)[/latex] a preto fuzzy číslo A je podľa Yagerovho indexu menšie ako B. Ďalej na obrázku (b) vidíme situáciu, kedy horizontálna súradnica ťažiska fuzzy čísla A je rovnaká ako horizontálna súradnica ťažiska fuzzy čísla B, t.j. [latex]F^{(1)}(A) = F^{(1)}(B)[/latex] a preto nevieme pomocou Yagerovho indexu určiť poradie fuzzy čísel. Na obrázkoch (c) a (d) sú zobrazené ďalšie fuzzy čísla u ktorých nevieme rozhodnúť o poradí Vidíme (viď obrázky 3 (c) a (d)), že Yagerov index je príliš nepostačujúcim opisom poradia fuzzy čísel. Jeho index je rovnaký pre veľkú skupinu fuzzy čísel. Ponúkajú sa dve možnosti, buď zvoliť inú metódu na porovnanie fuzzy čísel, ktorá lepšie charakterizuje hodnotu popísanú fuzzy číslom vzhľadom na optimalizačné kritérium alebo použiť na modelovanie časov spracovania intervaly, s ktorými je aritmetika a optimalizácia problémov oveľa jednoduchšia. Nech A = (a,b,c) je fuzzy číslo, potom k tomuto fuzzy číslu existuje množina <img src='http://s0.wp.com/latex.php?latex&bg=ffffff&fg=000000&s=0' alt='' title='' class='latex' />\mathbb B^{(1)} = \{B=(d,e,f)\,|\, F^{(1)}(A) = F^{(1)}(B), B\in\mathcal N(N)\}$ . Teda pre každé fuzzy číslo A existuje množina fuzzy čísel $\mathbb B^{(1)}$ , ktorá obsahuje také čísla, ktoré nevieme porovnať pomocou Yagerovho indexu. Ak $a,b,c,d,e,f\in N$ potom množina $\mathbb B^{(1)}$ obsahuje konečný počet fuzzy čísel. Čím je nosič množiny A väčší, tým je mohutnosť množiny $\mathbb B^{(1)}$ väčšia. Nech A = (a,b,c) je fuzzy číslo. Na Yagerov index $F^{(1)} = (a+b+c)/3$ , ktorý reprezentuje x-ovú súradnicu ťažiska fuzzy čísla, sa môžeme pozerať ako na hodnotu súčtu všetkých troch koeficientov, ktoré sú pred sčítaním vynásobené s koeficientom váh $w_1,w_2,w_3$ rovným hodnote jedna, $F^{(1)} = (w_1a+w_2b+w_3c)/3$ .

Autori Bector a Chandra prezentujú index porovnania $F^{(2)} = (a+2b+c)/4$ , ktorý oproti Yagerovmu indexu, pri ktorom boli váhy pri jednotlivých koeficientoch rovné hodnote jedna, majú váhu pri modálnej (strednej) hodnote fuzzy čísla dvojnásobnú. Ich pôvodnú myšlienku môžeme vidieť na obrázku 2(a) a využitie tohoto indexu môžeme nájsť všade tam, kde pri optimalizácií chceme využiť vlastnosti Yagerovho indexu, no chceme zároveň uprednostniť centrálnu hodnotu fuzzy čísla, teda hodnotu, pri ktorej sme si najviac istý s jej realizáciou. Na obrázku 4(a) môžeme vidieť spôsob, akým Bectorov index porovnáva fuzzy čísla. Na ďalšom obrázku 4(b) je zobrazená jedna z mnohých situácií, kedy index nedokáže určiť z dvoch fuzzy čísel to väčšie.

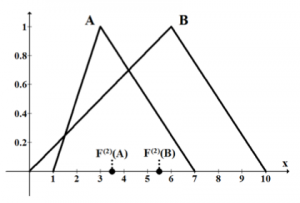
(a) Porovnanie fuzzy čísel pomocou Bectorovho indexu, fuzzy číslo A je vyhodnotené ako menšie ako B

(b) Fuzzy čísla pre ktoré nevieme určiť poradie, fuzzy čísla A, B sú vyhodnotené ako rovnaké

(c) Fuzzy čísla pre ktoré nevieme určiť poradie

(d) Fuzzy čísla pre ktoré nevieme určiť poradie
Fig. 4 Ukážka použitia Bectorovho indexu na porovnanie dvoch fuzzy čísel, kde na obrázku (a) vidíme, že hodna Bectorovho indexu je menšia pre fuzzy číslo A, t.j. $F^{(2)}(A) < F^{(2)}(B)[/latex]. Ďalej na obrázku (b) máme zobrazenú situáciu, kedy Bectorov index nevie rozhodnúť o poradí fuzzy čísel, t.j. [latex]F^{(2)}(A) = F^{(2)}(B)[/latex]. Na obrázkoch (c) a (d) sú zobrazené množiny fuzzy čísel, ktoré nadobúdajú rovnakú hodnotu Bectorovho indexu [latex]F^{(2)}(A)[/latex] pre fuzzy číslo A. Nech A = (a,b,c) je fuzzy číslo, potom k tomuto fuzzy číslu existuje množina <img src='http://s0.wp.com/latex.php?latex&bg=ffffff&fg=000000&s=0' alt='' title='' class='latex' />\mathbb B^{(2)} = \{B=(d,e,f)\,|\, F^{(2)}(A) = F^{(2)}(B), B\in\mathcal N(N)\}$ . Teda pre každé fuzzy číslo A existuje množina fuzzy čísel $\mathbb B^{(2)}$ , ktorá obsahuje také čísla, ktoré nevieme porovnať pomocou Bectorovho indexu. Ak $a,b,c,d,e,f\in N$ potom množina $\mathbb B^{(2)}$ obsahuje konečný počet fuzzy čísel. Aj keď nie je ešte dokázané, ale z experimentálnych pokusov vieme, že pre množiny $\mathbb B^{(1)}$ a $\mathbb B^{(2)}$ platí $|\mathbb B^{(1)}| \geq |\mathbb B^{(2)}|$ . Čím je nosič množiny A väčší, tým je mohutnosť množiny $\mathbb B^{(2)}$ väčšia.

McCahon a Lee stanovili dve kritéria. Prvé kritérium je totožné s Yagerovým indexom a ak vyhodnotí obe fuzzy čísla za totožné, potom druhé kritérium porovná rozptyl oboch fuzzy čísel. Tu si treba uvedomiť, že existujú dva spôsoby ako porovnať dve rozdielne fuzzy čísla s rovnakou strednou hodnotou. Buď prehlásime fuzzy číslo s menším rozptylom za väčšie alebo ho prehlásime za menšie. Toto rozhodnutie vyplýva zo zadania problému, čo dané fuzzy čísla modelujú a samotnej charakteristiky optimalizácie (minimalizácia, maximalizácia).

Na obrázku 5(a) vidíme dve fuzzy čísla, ktoré McCahonove a Leeove kritéria porovnajú tak, že fuzzy číslo A je vyhodnotené ako menšie ako fuzzy číslo B. To z toho dôvodu, že fuzzy čísla A a B predstavujú zisk a optimalizačná stratégia je optimistická, to znamená, že veríme viac tomu, že sa hodnoty budú realizovať bližšie ku strednej hodnote. Na pravom obrázku 5(b) je ukázaná jedna situácia z mnohých, kedy McCahonove a Leeove kritéria pokladajú obe fuzzy čísla za rovnaké.

(a) Porovnanie fuzzy čísel pomocou McCahonho a Leeovho indexu, fuzzy číslo A je vyhodnotené ako menšie ako B

(b) Fuzzy čísla pre ktoré nevieme určiť poradie, fuzzy čísla A, B sú vyhodnotené ako rovnaké
Fig. 5 Ukážka použitia McCahonho a Leeovho indexu na porovnanie dvoch fuzzy čísel, kde na obrázku (a) vidíme, že hodna indexu je menšia pre fuzzy číslo A, t.j. $F^{(3)}(A) < F^{(3)}(B)[/latex]. Ďalej na obrázku (b) máme zobrazenú situáciu, kedy McCahon index nevie rozhodnúť o poradí fuzzy čísel, t.j. [latex]F^{(3)}(A) = F^{(3)}(B)[/latex]. Nech A = (a,b,c) je fuzzy číslo, potom k tomuto fuzzy číslu existuje množina <img src='http://s0.wp.com/latex.php?latex&bg=ffffff&fg=000000&s=0' alt='' title='' class='latex' />\mathbb B^{(3)} = \{B=(d,e,f)\,|\, F^{(3)}(A) = F^{(3)}(B), B\in\mathcal N(N)\}$ . Množina $\mathbb B^{(3)}$ obsahuje fuzzy čísla, ktoré sú podľa Bectorovho indexu vyhodnotené ako rovné k číslu A. Ak $a,b,c,d,e,f\in N$ potom množina $\mathbb B^{(3)}$ obsahuje konečný počet fuzzy čísel. Podľa experimentálnych pokusov vieme, že $|\mathbb B^{(2)}| \geq |\mathbb B^{(3)}|$ .

Sakawa a Kubota použili na porovnanie fuzzy čísel A = (a,b,c) tri kritéria. Najskôr porovnávajú fuzzy čísla rovnako ako Bector, ak je ale Bectorov index rovnaký pre obe porovnávané fuzzy čísla, potom porovnajú modálne hodnoty oboch fuzzy čísel, väčšia modálna hodnota určuje väčšie fuzzy číslo. Ak sú ale aj modálne hodnoty rovnaké, potom posledné kritérium porovná nosiče fuzzy čísel. Ak sú rovné, potom sú fuzzy čísla vyhodnotené ako rovnaké. Tento index je rovnako ako Bectorov index viac zameraný na strednú (centrálnu) hodnotu fuzzy čísla. Tu sa pri treťom kritériu taktiež ponúka možnosť, že fuzzy číslo A s menším nosičom bude vyhodnotené ako väčšie. To za predpokladu, že modelujeme optimalizačný problému na tomto predpoklade.

Nech A = (a,b,c) je fuzzy číslo, potom k tomuto fuzzy číslu existuje množina $\mathbb B^{(4)} = \{B=(d,e,f)\,|\, F^{(4)}(A) = F^{(4)}(B), B\in\mathcal N(N)\}$ . Množina $\mathbb B^{(4)}$ obsahuje fuzzy čísla, ktoré sú podľa Sakawa a Kubotovho indexu vyhodnotené ako rovné k číslu A. Ak $a,b,c,d,e,f\in N$ potom množina $\mathbb B^{(4)}$ obsahuje jediné fuzzy číslo A.

Nech $w_1,w_2\geq 0$ a nech $w_1+w_2 = 1$ . Ak chceme dosiahnuť toho, aby agregačný index $F^{(5)}$ porovnával fuzzy čísla rovnako ako Yagerov index, stačí nastaviť hodnoty parametrov $w_1 = 1$ a $w_2 = 0$ . Takéto nastavenie parametrov ale vedie k veľkej početnosti fuzzy čísel, ktoré medzi sebou nevieme rozlíšiť. Čím je parameter $w_1$ menší, tým metóda menej porovnáva fuzzy čísla na základe informácie o ťažisku a viacej ich porovnáva na základe informácie o rozptyle hodnôt okolo ťažiska. Nech A = (a,b,c) je fuzzy číslo, potom k tomuto fuzzy číslu existuje množina $\mathbb B^{(5)} = \{B=(d,e,f)\,|\, F^{(5)}(A) = F^{(5)}(B), B\in\mathcal N(N)\}$ .

Množina $\mathbb B^{(5)}$ obsahuje fuzzy čísla, ktoré sú podľa agregačného indexu totožné s číslom A. Experimentálne je dokázané, že pre $w_1>0$ a $w_2>0$ je mohutnosť množiny $\mathbb B^{(5)}$ veľmi malá. Chengov index $F^{(6)}$ porovnáva fuzzy čísla podľa vzdialenosti ťažiska od počiatku súradnicovej sústavy. Na obrázku 6(a) je zobrazený spôsob porovnania dvoch fuzzy čísel pomocou Chengovho indexu. Ďalší obrázok 6(b) zobrazuje jednu z mnohých situácií, kedy index nedokáže určiť z dvoch fuzzy čísel to väčšie.

(a) Porovnanie fuzzy čísel pomocou Chengovho indexu, fuzzy číslo A je vyhodnotené ako menšie ako B

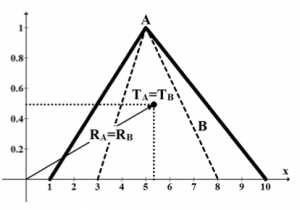
(b) Fuzzy čísla pre ktoré nevieme určiť poradie

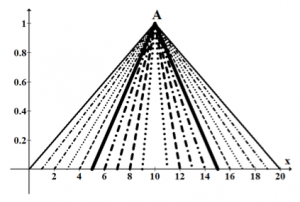
(c) Fuzzy čísla pre ktoré nevieme určiť poradie
Fig. 6 Ukážka použitia Chengovho indexu na porovnanie dvoch fuzzy čísel, kde na obrázku (a) vidíme, že hodna indexu je menšia pre fuzzy číslo A, t.j. $F^{(6)}(A) < F^{(6)}(B)[/latex]. Ďalej na obrázkoch (b) a (c) máme zobrazenú situáciu, kedy Chengov index nevie rozhodnúť o poradí fuzzy čísel, t.j. [latex]F^{(6)}(A) = F^{(6)}(B)[/latex]. Nech A=(a,b,c) je fuzzy číslo, potom k tomuto fuzzy číslu existuje množina <img src='http://s0.wp.com/latex.php?latex&bg=ffffff&fg=000000&s=0' alt='' title='' class='latex' />\mathbb B^{(6)} = \{B=(d,e,f)\,|\, F^{(6)}(A) = F^{(6)}(B), B\in\mathcal N(N)\}$ . Množina $\mathbb B^{(6)}$ obsahuje fuzzy čísla, ktoré sú podľa Chengovho indexu vyhodnotené ako rovné k číslu A. Ak $a,b,c,d,e,f\in N$ potom množina $\mathbb B^{(6)}$ obsahuje konečný počet fuzzy čísel. Experimentálne pokusy ukazujú, že $|\mathbb B^{(1)}| \geq |\mathbb B^{(2)}| \geq |\mathbb B^{(6)}|$ . Čím je nosič množiny A väčší, tým je mohutnosť množiny $\mathbb B^{(6)}$ väčšia.

Chuov a Tsaov index $F^{(7)}$ porovnáva fuzzy čísla na základe obsahu plochy vymedzenej ťažiskom fuzzy čísla a počiatkom súradnicovej sústavy. Obrázok 7(a) zobrazuje princíp porovnania dvoch fuzzy čísel, pričom fuzzy číslo A je vyhodnotené ako menšie ako fuzzy číslo B. Na obrázku 7(b) môžeme vidieť jednu z mnohých situácií, kedy Chuov a Tsaov index nevie rozhodnúť o poradí fuzzy čísel.

(a) Porovnanie fuzzy čísel pomocou Chuovho a Tsaovho indexu, fuzzy číslo A je vyhodnotené ako menšie ako B

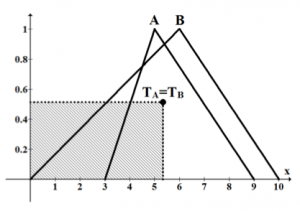
(b) Fuzzy čísla pre ktoré nevieme určiť poradie

(c) Fuzzy čísla pre ktoré nevieme určiť poradie

(d) Fuzzy čísla pre ktoré nevieme určiť poradie
Fig.7 Ukážka použitia Chuovho a Tsaovho indexu, pomocou ktorého porovnávame dve fuzzy čísla. Na obrázku (a) vidíme, že hodna indexu je menšia pre fuzzy číslo A, t.j. $F^{(7)}(A) < F^{(7)}(B)[/latex]. Ďalej na obrázkoch (b), (c) a (d) máme zobrazenú situáciu, kedy Chuov a Tsaov index nevie rozhodnúť o poradí fuzzy čísel, t.j. [latex]F^{(7)}(A) = F^{(7)}(B)[/latex]. Obrázky 7(c) a 7(d) zobrazujú celú sériu fuzzy čísel, ktoré index nevie porovnať. Nech A=(a,b,c) je fuzzy číslo, potom k tomuto fuzzy číslu existuje množina <img src='http://s0.wp.com/latex.php?latex&bg=ffffff&fg=000000&s=0' alt='' title='' class='latex' />\mathbb B^{(7)} = \{B=(d,e,f)\,|\, F^{(7)}(A) = F^{(7)}(B), B\in\mathcal N(N)\}$ . Množina $\mathbb B^{(7)}$ obsahuje fuzzy čísla, ktoré sú podľa Chuovho a Tsaovho indexu vyhodnotené ako rovné k fuzzy číslu A. Ak $a,b,c,d,e,f\in N$ potom množina $\mathbb B^{(7)}$ obsahuje konečný počet fuzzy čísel.

Experimentálne pokusy ukazujú, že $|\mathbb B^{(1)}| \geq |\mathbb B^{(2)}| \geq |\mathbb B^{(7)}| \geq |\mathbb B^{(6)}|$ . Chen a Chen počítajú index $F^{(8)}$ pomocou informácie o ťažisku a rozptylu. Na obrázku 8(a) je zobrazený spôsob akým Chenov a Chenov index porovnáva fuzzy čísla. Ďalší obrázok 8(b) zobrazuje situáciu, kedy index nedokáže určiť z dvoch fuzzy čísel to väčšie.

(a) Porovnanie fuzzy čísel pomocou Chenovho a Chenovho indexu, fuzzy číslo A je vyhodnotené ako menšie ako B

(b) Fuzzy čísla pre ktoré nevieme určiť poradie
Fig. 8 Ukážka použitia Chenovho a Chenovho indexu, pomocou ktorého porovnávame dve fuzzy čísla. Na obrázku (a) vidíme, že hodna indexu je menšia pre fuzzy číslo A, t.j. $F^{(8)}(A) < F^{(8)}(B)[/latex]. Ďalej na obrázkoch (b) máme zobrazenú situáciu, kedy Chenov a Chenov index nevie rozhodnúť o poradí fuzzy čísel, t.j. [latex]F^{(8)}(A) = F^{(8)}(B)[/latex]. Nech A=(a,b,c) je fuzzy číslo, potom k tomuto fuzzy číslu existuje množina <img src='http://s0.wp.com/latex.php?latex&bg=ffffff&fg=000000&s=0' alt='' title='' class='latex' />\mathbb B^{(8)} = \{B=(d,e,f)\,|\, F^{(8)}(A) = F^{(8)}(B), B\in\mathcal N(N) \}$ . Množina $\mathbb B^{(8)}$ obsahuje fuzzy čísla, ktoré sú podľa Chen a Chenovho indexu vyhodnotené ako rovné k fuzzy číslu A. Ak $a,b,c,d,e,f\in N$ potom množina $\mathbb B^{(8)}$ obsahuje konečný počet fuzzy čísel. Experimentálne pokusy ukazujú, že $|\mathbb B^{(1)}| \geq |\mathbb B^{(2)}| \geq |\mathbb B^{(7)}| \geq |\mathbb B^{(6)}| \geq |\mathbb B^{(8)}|$ .

Indexy Yager, Bector, Cheng, Chuov a Tsaov, nemôžeme použiť v optimalizácií, kde záleží na rozptyle hodnôt okolo priemernej hodnoty (ťažiska). Dôvodom je, že mohutnosť množiny $B^{(i)}$ , pre i=1,2,7,8, je pre tieto indexy veľká.

5 Záver

Článok sa venoval problematike porovnania fuzzy čísel. Definoval desať známych metód porovnania fuzzy čísel. Zamerali sme sa na \textit{neúspešnosť}, s akou porovnávajú tieto metódy fuzzy čísla. Pod pojmom neúspešnosť si môžeme predstaviť počet rôznych fuzzy čísel, ktoré daná metóda považuje za totožné. Predpokladáme, že čím je táto neúspešnosť menšia, tým je metóda viac vyhradená pre určitý druh optimalizácie (minimalizácia, maximalizácia, optimistické riešenie, pesimistické riešenie, realistické riešenie).

Yagerová metóda ovplyvnila veľkú skupinu vedeckých pracovníkov a bola počiatkom novej vetvy metód porovnania fuzzy čísel. Je zrejmé, že táto metóda, spoločne s Bectorovou, Chengovou a Chuo-Tsaovou metódou je nevhodná pre optimalizácie, pri ktorých chceme rozlíšiť fuzzy čísla vzhľadom na veľkosť podstavy, pričom predpokladom je veľké opakovanie fuzzy čísel s rovnakou strednou hodnotou.

Tu doporučujeme použiť radšej agregačný prístup, ktorým môžeme spojiť vážené dielčie indexy porovnania (napr. index ťažiska a index rozptylu), alebo McCahon-Leeov prístup, ktorý porovnáva fuzzy čísla lexikograficky (ťažisko a rozptyl). Otázkou ostáva pre aké typy optimalizačných problémov sú vhodné indexy porovnania ako Yagerov, Bectorov index. Tieto indexy sa vyznačujú veľkou neúspešnosťou porovnania fuzzy čísel.

Naopak, vzhľadom na neúspešnosť porovnania sa ideálne umiestnil Sakawa-Kubotov lexikografický prístup. Pre tieto dva prístupy by bolo zaujímavé zistiť, pre ktoré typy optimalizačných problémov sa hodia najviac. Ďalej, vzhľadom na väčšiu neúspešnosť, sa umiestnili Chen-Chenov a McCahon-Leeov index. Výsledok experimentu môžeme zapísať nasledujúco:

$\text{[math]}$ |\mathbb B^{(4)}|<|\mathbb B^{(8)}|<|\mathbb B^{(3)}|=|\mathbb B^{(5)}|<|\mathbb B^{(6)}|<|\mathbb B^{(7)}|<|\mathbb B^{(2)}|<|\mathbb B^{(1)}|[/latex]

Poďakovanie

Táto práca vznikla s podporou grantovej agentúry VEGA vrámci riešenia projektu 1/0374/11 “Modelovanie a optimalizácia mobility a infraštruktúry v logistických sieťach.”.

Literatúra

D. Dubois and H. Prade. Operations on fuzzy numbers. The International Journal of Systems Sciences, 9:613–626, 1978.

R. Jain. Decision-making in the presence of fuzzy vari- ables. IEEE Transactions on Systems, Man and Cybernetics, 6, pages 698–703, 1976.

J.H. Lee and H. Lee-Kwang. A method for ranking fuzzily fuzzy numbers. The Nineth IEEE International Conference on Fuzzy Systems, 1:71–76, 2000.

C.S. McCahon and E.S. Lee. Fuzzy job sequencing for a flow shop. European Journal of Operational Research, 1992.

S.H. Nasseri and M. Sohrabi. Hadi‘s method and it‘s advan-
tage in ranking fuzzy numbers. Australian Jornal of Basic and Applied Sciences, 4(10), pages 4630–4637, 2010.

N. Ramli and D. Mohamad. A comparative analysis of cen- troid methods in ranking fuzzy numbers. European Journal of Scientific Research, 28(3):492–501, 2009.

R. Sakawa, M. Kubota. Fuzzy programming for multiobjec- tive job shop scheduling with fuzzy processing time and fuzzy duedate through genetic algorithms. European Journal of Op- erations Research, 120:393–407, 2000.

R.R. Yager. On a general class of fuzy connectives. Fuzzy Sets and Systems, 4(6), pages 235–242, 1980.

L.A. Zadeh. Fuzzy sets. Information and Control 8 (3), page 338–353, 1965.