Problém rovnomerných rozvrhov a stochastické programovanie

22. August, 2011, Autor článku: Ladovský Tomáš, Informačné technológie
Ročník 4, číslo 8 Pridať príspevok

Článok sa venuje problému tvorby rovnomerných rozvrhov pri neistote. Tieto rovnomerné rozvrhy môžeme zovšeobecniť a riešiť ako problém rovnomernosti riadkových súčtov stĺpcovo permutovanej matice. Nás zaujíma výhradne dvojriadkový variant problému, pričom prvky matice sú modelované náhodnými premennými normálneho rozdelenia pravdepodobnosti. Dvojriadkovú stochastickú maticu vieme riešiť exaktne transformáciou na bivalentný program známy pod názvom stochastická úloha o batohu. Pre každý prezentovaný problém je riešený ilustračný príklad.

1. Úvod

V tomto článku rozumieme pod pojmom tvorba rozvrhu alebo rozvrhovanie proces rozhodovania, ktorý sa používa vo výrobnom priemysle, vo verejnej doprave a v iných odvetviach a službách. Pracuje s prideľovaním aktivít k zdrojom nad danými časovými periódami a snaží sa optimalizovať jednu alebo viac kritériálnych funkcií tak, aby boli splnené všetky podmienky priradené k jednotlivým aktivitám a zdrojom. Z iného pohľadu je tvorba rozvrhov problémom časového plánovania a kombinatorickej optimalizácie. To sú problémy, v ktorých vystupujú diskrétne premenné a v ktorých množina prípustných riešení je konečná. V každom z týchto problémov sa skrýva možnosť kombinatorickej explózie.

Rozvrh je súbor údajov, z ktorého je zrejmé, v ktorých časových intervaloch sa majú jednotlivé aktivity realizovať na ktorých zdrojoch. Zdrojmi môžu byť vodiči autobusov, stroje v dielni, viacnásobné/viacjadrové procesory, dopravné prostriedky, robotníci na pracovisku a veľa iného. Aktivitami môžu byť turnusy¹ v autobusovej doprave, úlohy (operácie) vo výrobnom procese, vykonávanie počítačových programov, etapy pri stavebnom projekte a iné. Každá aktivita má naplánovanú dobu trvania.

V reálnom živote sa stretávame so zrovnomerňovaním pracovných zaťažení/výkonov strojov/vodičov za dané časové (periodické) obdobie rozvrhovania. Aby sme vedeli optimalizovať rovnomernosť rozvrhov, potrebujeme poznať mieru nerovnomernosti [2], ktorá je jednou z optimalizovaných kritériálnych funkcií a môže nadobúdať nasledujúci tvar

$f_{dev}(x_1, \dots, x_m) = \frac{1}{m} \sum_{i=1}^{m}\frac{|x_i-\bar{x}|}{\bar{x}}$

(1)

Za predpokladu, že vytvárame rozvrh vo verejnej doprave, predstavujú jednotlivé premenné x₁ až x_m plánované kumulované pracovné zaťaženia m vodičov a $\bar{x}$ je ideálnym pracovným zaťažením. V tomto prípade priemernou hodnotou, ktorú spočítame ako

$\bar{x} = \frac{1}{m} \sum_{i=1}^{m} x_i$

(2)

Rozvrhy, ktoré vznikli optimalizáciou miery nerovnomernosti, nazývame rovnomernými rozvrhmi. Vzhľadom na známu Grahamovu [1] klasifikáciu ide o neštandardný typ rozvrhov

2. Matematická formulácia

Rovnomerné rozvrhy môžeme zovšeobecniť a matematicky formulovať ako kombinatorický problém rovnomernosti riadkových súčtov stĺpcovo permutovanej matice, ktorý anglicky označujeme ako matrix permutation problem $\mathcal{MPP}$ [4]. Vhodným preusporiadaním stĺpcov matice môžeme docieliť väčšiu rovnomernosť riadkových súčtov matice/rozvrhu.

Definícia 2.1. (Matrix permutation problem [3])

Nech $\mathcal M=\{1,2,\dots,m\}$ a $\mathcal N=\{1,2,\dots,n\}$ sú konečné neprázdne množiny a nech $\mathbb A=(a_{ij})\in\mathfrak R^{m\times n}$ je reálna matica rozmeru $m\times n$ . Hľadá sa taká matica permutácií $\Psi = (\psi_j)_{j\in N}$ stĺpcov matice $\mathbb A$ pre ktorú platí:

$\min\Big\{ f(s^{\psi}_1,s^{\psi}_2,\dots,s^{\psi}_m) | s^{\psi}_i=\sum_{j\in\mathcal N} a_{\psi_{ij},j},\forall i\in\mathcal M,$

$\psi_j = (\psi_{1j},\psi_{2j} \dots ,\psi_{mj}) \in \Pi(\mathcal M),\forall j\in\mathcal N \Big\}$

kde f je nejaká miera nerovnomernosti vektora reálnych čísel, $s^{\psi}_i$ je i-ty riadkový súčet matice ${\mathrm A}^\psi$ a $\Pi(\mathcal M)$ je množina všetkých permutácií množiny $\mathcal M$ . Riešením takto formulovanej úlohy $\mathcal{MPP}$ je matica $latex {\mathbb A}^\psi = (a_{\psi_{ij},j})

$\mathcal{MPP}$ je zložitosti $O((m!)^n)$ . Z tohoto dôvodu sú exaktne riešiteľné len veľmi malé inštancie. Na riešenie veľkých inštancií môžeme použiť heuristické metódy. Najznámejšou a najvhodnejšou heuristickou metódou, ktorá je veľmi rýchla a dosahuje veľmi dobré výsledky, je stochastická-dekompozičná metóda [3,4].

Príklad 2.1. (Rozpisovanie služieb vodičom autobusov, alias (MPP))

Majme 4 vodičov autobusov a 5 pracovných dní. Pre každý pracovný deň majú byť pridelené 4 turnusy, pričom prvok $a_{ij}$ matice $\mathbb A=(a_{ij}\in\mathfrak R)$ zodpovedá pracovnému času [min] i-teho turnusu v j-ty deň a vektor $S = (s_1,s_2,s_3,s_4)^T$ predstavuje štyri riadkové súčty matice $\mathbb A$

$\mathbb A=\left( \begin{array}{c c c c c} 660 & 540 & 530 & 460 & 680 \\ 630 & 500 & 570 & 630 & 710 \\ 510 & 640 & 680 & 580 & 650 \\ 450 & 460 & 540 & 450 & 680 \end{array} \right)$

$S = \left( \begin{array}{c} 2870 \\ 3040 \\ 3060 \\ 2580 \end{array} \right)$

(3)

Hodnota ideálneho kumulovaného výkonu vodiča je podľa (2) rovná hodnote $\bar{s} = 2887,5$ . Tvorca rozvrhu chce priradiť vodičom turnusy na jednotlivé dni tak, aby hodnota miery nerovnomernosti (1) bola minimálna. Ak ich priradí každý deň rovnako, tak že i-ty vodič dostane priradený i-ty turnus, t.j. $\psi_{ij} = i$ , tak je miera nerovnomernosti rovná hodnote $f_{dev}=0.056$ s odpovedajúcimi riadkovými súčtami S (3). Hodnota miery nerovnomernosti nás informuje o tom, že týždenné výkony vodičov sú priemerne odchýlené od ideálnej hodnoty o 5,6%. Rozvrh môžeme vidieť na obrázku 1(a) a riadkové súčty na obrázku 1(b).

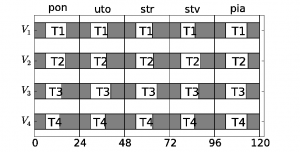
(a) Nerovnomerný rozvrh – týždenný

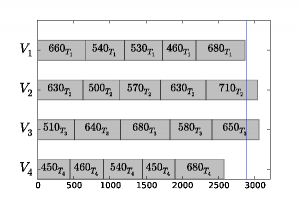
(b) Nerovnomerný rozvrh – kumulované pracovné časy

Obr. 1: Nezrovnomernený rozvrh služieb vodičov autobusov. Modrá horizontálna čiara predstavuje ideálny kumulovaný výkon vodiča $\bar{s}$

Teraz tvorca rozvrhu použije stochastickú-dekompozičnú metódu [3,4] a pomocou nej vygeneruje nasledovnú maticu permutácií $\Psi$ , výsledný rozvrh reprezentovaný maticou $\mathbb A^{\psi}$ a vektor riadkových súčtov $S^{\psi}$ matice $\mathbb A^{\psi}$ .

$\Psi=\left( \begin{array}{c c c c c} 4 & 3 & 4 & 3 & 4 \\ 3 & 2 & 2 & 2 & 1 \\ 2 & 4 & 3 & 1 & 3 \\ 1 & 1 & 1 & 4 & 2 \end{array} \right)$

$\mathbb A^{\psi}=\left( \begin{array}{c c c c c} 450 & 640 & 540 & 580 & 680 \\ 510 & 500 & 570 & 630 & 680 \\ 630 & 460 & 680 & 460 & 650 \\ 660 & 540 & 530 & 450 & 710 \end{array} \right)$

$S^{\psi} = \left( \begin{array}{c} 2890 \\ 2890 \\ 2880 \\ 2890 \end{array} \right)$

(4)

Pre tento rozvrh získavame nasledujúcu hodnotu miery nerovnomernosti $f_{dev}=0.001$ s odpovedajúcimi riadkovými súčtami $S^{\psi}$ (4). Vidíme, že rozvrh získaní heuristickou metódou je viac zrovnomernený. Rozvrh môžeme vidieť na obrázku 2(a) a riadkové súčty na obrázku 2(b).

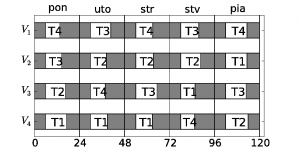
(a) Rovnomerný rozvrh – týždenný

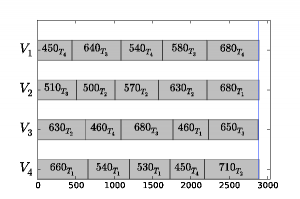
(b) Rovnomerný rozvrh – kumulované pracovné časy

Obr. 2: Zrovnomernený rozvrh služieb vodičov autobusov. Modrá horizontálna čiara predstavuje ideálny kumulovaný výkon vodiča $\bar{s}$

Veľmi zaujímavé varianta problému ( ${\mathcal MPP}$ ) vzniká pre dvojriadkovú variantu matice $\mathbb A$. Exaktné riešenie ${\mathcal MPP2r}$ problému môže poslúžiť v heuristických metódach na získanie dobrého riešenia problému ${\mathcal MPP}$ . Nasledujúci text objasňuje problematiku riešenia problému ${\mathcal MPP2r}$ pomocou klasickej úlohy o batohu.

3. Dvojriadková matica

Klasická úloha o batohu ${\mathcal KUB}$ je jednou z najznámejších a najpoužívanejších úloh matematického lineárneho programovania a tvorí jadro mnohých heuristických metód. Jej matematická formulácia je nasledovná.

Definícia 3.1. (Klasická úloha o batohu KUB)

Úlohu o batohu môžeme formulovať ako úlohu, v ktorej máme predmety rôznych cien a hmotností zabaliť do batohu tak, aby jeho hodnota bola čo možno najväčšia a nebola prekročená jeho nosnosť. Nech N, |N| = n je konečná množina, c je n-prvkový vektor cien predmetov, a je n-prvkový vektor hmotností predmetov, b je nosnosť batohu a x je n-prvkový vektor rozhodovacích premenných. Potom úlohu o batohu možno formulovať ako nasledujúcu úlohu bivalentného lineárneho programovania.

$\left . \begin{array}{c} \max Z = \sum_{j\in N}{c_j x_j} \\ s.t. \\ \sum_{j\in N}a_j x_j \leq b \\ x_j\in\{0,1\}, pre \quad \forall j\in N \end{array} \right \}$

(5)

Problém rovnomernosti riadkových súčtov stĺpcovo permutovanej \textit{dvojriadkovej matice} ${\mathcal MPP2r}$ môžeme exaktne riešiť pomocou nie zložitej transformácie na klasickú úlohu o batohu ${\mathcal KUB}$ .

Veta 3.1. (Transformácia ${\mathcal MPP2r}$ na ${\mathcal KUB}$ )

Pre danú maticu $\mathbb D = (d_{ij})$ typu $2\times n$ a maticu permutácií $\Psi = (\psi_j)_{j\in N}$ množiny $\mathcal M=\{1,2\}$ môžeme úlohu $layex {\mathcal MPP2r}$ pretransformovať na klasickú úlohu o batohu pomocou substitúcie

$c_j = a_j = d_{1j}-d_{2j},\quad\text{pre}\quad \forall j = 1,2,\dots, n$

(6)

$b = \frac{1}{2}\sum_{j=1}^{n} (d_{1j}-d_{2j})$

(7)

kde vektor rozhodnutí $x = (x_1, x_2, \dots, x_n)$ priradenia predmetu do batohu formulujeme ako

$\psi_j = \left\{ \begin{array}{c} (1,2), \text{vlozime j-ty predmet do batohu, t.j. } x_j = 1 \\ (2,1), \text{nevlozime j-ty predmet do batohu, t.j. } x_j = 0 \end{array} \right.$

Dôkaz (Transformácia ${\mathcal MPP2r}$ na ${\mathcal KUB}$ )

Majme maticu $\mathbb D=(d_{ij})$ rozmeru $2\times n$ , pre ktorú hodnotu ideálneho riadkového súčtu spočítame ako

$\bar{s} = \frac{1}{2}\sum_{j=1}^{n} (d_{1j} + d_{2j})$

Nech $\Psi = (\psi_j)_{j\in N}$ je matica permutácií a nech vektor $x = (x_1, x_2, \dots, x_n)$ predstavuje rozhodnutia, ktoré môžeme formulovať ako:

$x_j = \left \{ \begin{array}{c} 1 \text{ potom } \psi_{j} = (1,2) \\ 0 \text{ potom } \psi_{j} = (2,1) \end{array} \right.$

Aby boli riadkové súčty matice čo najrovnomernejšie, alebo aby sa v ideálnom prípade rovnali ideálnemu riadkovému súčtu, potom musí urobiť tvorca rozvrhu také rozhodnutia x, pre ktoré platí nasledujúca rovnosť

$\sum_{j=1}^{n}d_{1j}x_j + \sum_{j=1}^{n}d_{2j}(1-x_j) = \bar{s},$

ktorú môžeme po dosadení $\bar{s}$ a pomocou substitúcií

$c_j = a_j = d_{1j}-d_{2j} a b = \frac{1}{2}\sum_{j=1}^{n} (d_{1j}-d_{2j})$

prepísať na tvar

$\sum_{j=1}^{n}c_jx_j = b$

Bez ujmy na všeobecnosti môžeme rovnosť rozpísať na nerovnosti

$\sum_{j=1}^{n}a_jx_j \leq b$

(8)

$\sum_{j=1}^{n}c_jx_j - b \geq 0$

(8)

Aby sme úspešne transformovali zadanú úlohu na model úlohy o batohu, môžeme z ľavej strany nerovnosti (9) vypustiť konštantu b a použiť nerovnosť ako účelovú funkciu, ktorú maximalixujeme. Prvá nerovnosť (8) zaručuje, že súčet prvého riadku nepresiahne hodnotu b. Druhá nerovnosť (9) (účelová funkcia) sa naopak pokúša naakumulovať súčet prvého riadku čo najtesnejšie k hodnote b. Po takýchto úpravách získavame model klasickej úlohy o batohu (5).

Príklad 3.1. (Ilustračný príklad problému ${\mathcal MPP2r}$ )

Príkladom aplikácie ${\mathcal KUB}$ pri tvorbe rovnomerných rozvrhov môže byť nasledujúca úloha: Nech elementy matice $\mathbb D=(d_{ij})$ rozmeru $2\times 5$ predstavujú pracovné časy i-teho turnusu, ktorý máme prejsť v j-ty deň.

$\mathbb D=\left( \begin{array}{c c c c c} 35 & 45 & 25 & 45 & 20\\ 25 & 30 & 22 & 30 & 35 \end{array} \right)$

Pre každý deň 5-dňového obdobia máme rozhodnúť o tom, ktorému z dvojice vodičov pridelíme ktorý turnus, tak aby celkové kumulované výkony oboch vodičov, boli čo najviac rovné ideálnemu výkonu

$\bar{s} = \frac{1}{2}\sum_{j=1}^{n} (d_{1j} + d_{2j}) = 156$

za celé časové obdobie. Nech vektor $x$ predstavuje rozhodnutia, ktoré môžeme formulovať ako: x_j

1 – Ak sa rozhodneme priradiť prvému vodičovi prvý turnus s časom spracovania $d_{1j}$ a druhému vodičovi druhý turnus s časom spracovania $d_{2j}$ v j-ty pracovný deň,
0 – Ak sa rozhodneme priradiť prvému vodičovi druhý turnus s časom spracovania $d_{2j}$ a druhému vodičovi prvý turnus s časom spracovania $d_{1j}$ v j-ty pracovný deň.

Nech usporiadaná pätica c = a = (10,15,3,15,-15) predstavuje cenu a váhu predmetu a b=14 predstavuje nosnosť batohu. Riešením úlohy (5) získame nasledujúcu usporiadanú päticu rozhodnutí x = (1, 1, 1, 0, 1). Potom matica permutácií $\Psi$ je rovná

$\Psi=\left( \begin{array}{c c c c c} 1 & 1 & 1 & 2 & 1\\ 2 & 2 & 2 & 1 & 2 \end{array} \right)$

a riadkové súčty sú rovné $s^{\Psi} = (155, 157)$ .

4. Neistá veľkosť aktivít

V praxi dochádza k odchýleniu plánovaných pracovných časov turnusov, od skutočne sa zrealizovaných časov jázd vodičov, čo môže mať zásadný dopad na celkovú rovnomernosť rozvrhu. Tento nedostatok sa pokúsime vyriešiť robustnejším modelovaním pracovných časov turnusov. Ak máme k dispozícií štatistiku minulých realizácií turnusov, tak môžeme pomocou teórie pravdepodobnosti modelovať plánované časy turnusov pomocou náhodných premenných. Ak štatistiku k dispozícií nemáme, tak pravdepodobnostné rozdelenia navrhujeme pomocou dosiahnutých skúseností v danom obore, čo je prípad nasledujúceho textu.

Pravdepodobné správanie sa náhodných premenných môžeme popísať zákonom rozdelenia pravdepodobnosti. Kvôli jednoduchosti sa obmedzíme v nasledujúcom texte na normálne rozdelenie pravdepodobnosti $N(\mu,\sigma^2)$ [5].

Definícia 4.1. (Normálne rozdelenie pravdepodobnosti)

Náhodná premenná X má normálne rozdelenie pravdepodobnosti s parametrami $\mu$ a $\sigma^2$ , ak jej funkcia hustoty pravdepodobnosti (pdf) je

$f(x) = \frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}, \quad x\in\mathcal R$

(10)

Zapisujeme: $X\sim N(\mu,\sigma^2)$ . Parametrami normálneho rozdelenia sú: $\mu$ – stredná hodnota a $\sigma$ – smerodajná odchýlka.

Pri transformácií ${\mathcal MPP2r}$ problému na ${\mathcal KUB}$ sme použili operácie sčítania a odčítania dvoch alebo viacerých reálnych hodnôt. V nasledujúcom texte ale potrebujem tieto operácie vykonávať s náhodnými premennými. Nasledujúca veta formalizuje spôsob sčítania (odčítania) dvoch náhodných premenných.

Veta 4.1. (Vlastnosti normálneho rozdelenia [6, 7])

Ak X a Y sú nezávislé náhodné premenné normálneho rozdelenia, potom X+Y je taktiež normálneho rozdelenia, t.j. ak $X\sim N(\mu, \sigma^2)$ a $Y\sim N(\nu, \tau^2)$ a X a Y sú nezávislé, potom $Z = X+Y \sim N(\mu+\nu, \sigma^2+\tau^2)$ .

Ak X je náhodná premenná normálneho rozdelenia, t.j. $X\sim N(\mu, \sigma^2)$ , potom lineárna forma aX+b, pre $a,b\in\mathfrak R$ , je taktiež normálneho rozdelenia, t.j. $aX+b\sim N(a\mu+b, a^2\sigma^2)$ .

Ak X a Y sú nezávislé náhodné premenné normálneho rozdelenia, potom $aX+bY, a,b\in\mathfrak R$ je taktiež normálneho rozdelenia, t.j. ak $X\sim N(\mu, \sigma^2)$ a $Y\sim N(\nu, \tau^2)$ a X a Y sú nezávislé, potom $Z = aX+bY \sim N(a\mu+b\nu, a^2\sigma^2+b^2\tau^2)$ .

Dôkaz. (Vlastnosti normálneho rozdelenia)

Dôkaz môžeme nájsť na internetovej stránke otvorenej slovenskej online encyklopédie so slobodným obsahom [6], [7].

V predošlom texte sme v ${\mathcal MPP2r}$ probléme modelovali pracovné časy turnusov pomocou reálnych čísel. Následne sme tento problém transformovali pomocou vety 3.1 na klasickú úlohu o batohu ${\mathcal KUB}$ s reálnymi koeficientami v účelovej funkcii a podmienkach. Teraz ale chceme modelovať v ${\mathcal MPP2r}$ probléme pracovné časy turnusov pomocou náhodných premenných normálneho rozdelenia (4.1) a transformovať ho na stochastickú úlohu o batohu ${\mathcal SUB}$ , ktorú vieme riešiť pomocou teórie stochastického programovania [2]. Pre ľahšie porozumenie problematiky uvádzame nasledujúci ilustračný príklad.

Príklad 4.1. (Ilustračný príklad stochastického ${\mathcal MPP2r}$ problému)

Uvažujme rozvrhovaciu úlohu (príklad 3.1) pre dvoch vodičov na týždeň (5 pracovných dní), kde prvok $d_{ij}$ matice $\mathbb D$ rozmeru $2\times 5$ predstavuje \textbf{plánované} pracovné časy i-teho turnusu, ktorý máme prejsť v j-ty deň

$\mathbb D = \left( \begin{array}{ccccc} 35 & 45 & 25 & 45 & 20 \\ 25 & 30 & 22 & 30 & 35 \end{array} \right)$

Pre každý deň päť dňového obdobia máme rozhodnúť o tom, v akom poradí pridelíme dvojicu turnusov dvojici vodičov, tak aby celkové kumulované výkony oboch vodičov, boli čo najviac rovné ideálnemu výkonu za celé časové obdobie.

Nech $\mathcal M = \{1,2\}$ je množina indexov vodičov a nech $\mathcal N = \{1,2,3,4,5\}$ je množina indexov dní. Modelujme predpokladané odchýlky plánovaných časov (viď. matica $\mathbb D$ ) od skutočne sa zrealizovaných časov jázd vodičov autobusov pomocou náhodnej matice $\tilde{\mathbb U} = (\tilde{u}_{ij})$ rozmeru $2\times 5$ a predpokladajme, že pre každý nasledujúci deň je náš odhad pracovných časov turnusov viac nepresný. Prvkami $\tilde{u}_{ij}$ tejto matice sú náhodné premenné normálneho rozdelenia, tzv.

$dist\,\, \tilde{u}_{ij}\sim N(\mu,\sigma^2_j),\quad \forall (i,j)\in\mathcal M\times\mathcal N,$

(11)

kde $\mu = 0$ a $\sigma^2_j = 2j - 1, \forall j\in\mathcal N$ .

Pretransformujme teraz ${\mathcal MPP2r}$ problém na stochastickú úlohu o batohu ${\mathcal SUB}$ pomocou nasledujúcich výpočtov:

1. Cenu a váhu j-teho predmetu vyjadríme ako

$c_j(\tilde{\xi}) = a_j(\tilde{\xi}) = d_{1j} - d_{2j} + \tilde{\xi}_j,\quad \forall j\in\mathcal N$

kde $\tilde{\xi} = (\tilde{\xi}_1,\tilde{\xi}_2,\dots,\tilde{\xi}_5)$ je náhodný vektor s realizáciami $\xi = (\xi_1,\xi_2,\dots,\xi_5)$ , ktorého prvky spočítame ako

$\tilde{\xi}_j = \tilde{u}_{1j} - \tilde{u}_{2j},\quad \forall j\in\mathcal N$

a podľa vety 4.1 platí $\tilde{\xi}_j\sim N(0,2\sigma^2_j), \forall j\in\mathcal N$ . Pretože je normálne rozdelenie neohraničené, obmedzíme sa s realizáciami $\xi$ náhodného vektora $\tilde{\xi}$ na 99% konfidenčné intervaly

$\xi_j\in [\mu - 2.576\sigma_j, \mu + 2.576\sigma_j],\quad \forall j\in\mathcal N$

(12)

Teraz môžeme vektor $c(\tilde{\xi})$ zapísať ako

$c(\tilde{\xi}) = (10 + \tilde{\xi}_1, 15 + \tilde{\xi}_2, 3 + \tilde{\xi}_3, 15 + \tilde{\xi}_4, -15 + \tilde{\xi}_5)$

a plati

$c_j(\tilde{\xi}) \sim N(d_{1j} - d_{2j}, 2\sigma^2_j),\quad\forall j\in\mathcal N$

2. Nosnosť batohu spočítame ako

$b(\tilde{\xi}) = \frac{1}{2}\sum_{j\in\mathcal N} c_j(\tilde{\xi}) = 14 + \frac{1}{2}\sum_{j\in\mathcal N} \tilde{\xi}_j$

a plati

$b(\tilde{\xi})\sim N\left(\frac{1}{2}\sum_{j\in\mathcal N} c_j, \frac{1}{2}\sum_{j\in\mathcal N} \sigma^2_j\right)$

Matematický model stochastickej úlohy o batohu ${\mathcal SUB}$ môžeme teraz formulovať ako:

$\left . \begin{array}{c} \max Z = E_{\tilde{\xi}}[\sum_{j\in\mathcal N}{ c_j(\tilde{\xi}) x_j }] \\ s.t. \\ \sum_{j\in\mathcal N} a_j(\tilde{\xi}) x_j \leq b(\tilde{\xi}) \\ x_j\in\{0,1\}, pre \forall j\in\mathcal N \end{array} \right \}$

(13)

kde $E_{\tilde{\xi}}$ predstavuje priemernú hodnotu vzhľadom na pravdepodobnostné rozdelenie $\tilde{\xi}$ .

Aby sme si pri riešení problému (13) ušetrili nepríjemnosti spojené so spojitým normálnym rozdelením, aproximujme toto spojité rozdelenie diskrétnym [2]. Pre tento účel

generujme pre každé $j\in\mathcal N$ súbor realizácií $\xi^u_j, u = 1,\dots,K$ obmedzených na 99% konfidenčné intervaly. Veľkosť súborov je K = 15000;
ekvidištančne rozdeľme 99% konfidenčné intervaly (12) na r=15 podintervalov, r je počet realizácií $\tilde{\xi} = (\tilde{\xi}_1,\tilde{\xi}_2,\dots,\tilde{\xi}_5)$
pre každý podinterval $I_{jv}$ , kde $v=1,\dots,r,\, j\in\mathcal N$ spočítajme aritmetický priemer $\bar{\xi}_j^v = q_{jv} / k_{jv}$ , kde $q_{jv}$ a $k_{jv}$ sú porade súčet a počet realizácií $\xi^u_j$ obsiahnutých v $I_{jv}$
pre každý podinterval $I_{jv}$ spočítajme relatívnu frekvenciu $p_{jv} = k_{jv}/K$

Tieto diskrétne pravdepodobnostné rozdelenia

$\{(\bar{\xi}^v_j, p_{jv}), v=1,\dots,r\},\text{ kde }j\in\mathcal N,$

(14)

sú ďalej použité ako aproximácie daných normálnych rozdelení a môžeme ich vidieť na obrázku 3.

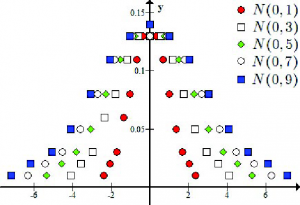
Obr. 3: Diskrétne pravdepodobnostné rozdelenia, ktoré vznikli diskretizáciou spojitých normálnych rozdelení (11), ktorých realizácie patria do 99% konfidenčných intervalov (12).

Nech $\mathcal R = \{1,2,\dots, r\}$ je množina indexov realizácií $\xi$ náhodného vektora $\tilde{\xi}$ diskrétneho pravdepodobnostného rozdelenia (14). Teraz môžeme prepísať stochastickú úlohu o batohu (13) na klasický deterministický bivalentný problém

$\left . \begin{array}{c} max Z = \sum_{v\in\mathcal R} p_v \sum_{j\in\mathcal N} c_j(\xi^v) x_j \\ s.t. \\ \sum_{j\in\mathcal N} a_j(\xi^v) x_j \leq b(\xi^v), \quad\forall v\in\mathcal R \\ x_j\in\{0,1\}, pre \forall j\in\mathcal N \end{array} \right \}$

(15)

kde vzhľadom na vzájomnú nezávislosť prvkov náhodného vektora $\tilde{\xi}$ , môžeme vypočítať pravdepodobnosť realizácie $\xi^v$ ako

$p_v = \prod_{j\in\mathcal N} p_{jv},\quad \forall v\in\mathcal R$

Riešením stochastického problému (15) je vektor rozhodnutí x = (1,1,1,0,1), pre ktorý je matica permutácií $\Psi$ je rovná

$\Psi=\left( \begin{array}{c c c c c} 1 & 1 & 1 & 2 & 1\\ 2 & 2 & 2 & 1 & 2 \end{array} \right)$

Poznámka 1. (Ilustračný príklad stochastického ${\mathcal MPP2r}$ problému)

Z (11) vidíme, že pre každý nasledujúci deň rozvrhovania je väčší rozptyl normálneho rozdelenia pravdepodobnosti, čo vedie k predpokladu, že pre každý nasledujúci deň je náš odhad pracovných časov turnusov viac nepresný. Otázkou ostáva, či stratégia ktorá pre každý nasledujúci deň zväčšuje tento rozptyl, alebo stratégia ktorá zmenšovať tento rozptyl, vedie na optimálny rozvrh vzhľadom na optimalizačné kritérium

$f_{dev} = \left( f_{dev}(S^P) - f_{dev}(S^R) \right)^2,$

kde $f_{dev}(.)$ je miera nerovnomernosti (1) a $S^P$ je vektor riadkových súčtov rozvrhu s naplánovanými časmi turnusov a $S^R$ je vektor skutočne sa zrealizovaných časov jázd vodičov.

Od počtu realizácií r náhodného vektora $\tilde{\xi}$ v j-tom dni sa môže stať program (15) príliš veľkým a komplexným.

5. Záver

Článok sa venoval problematike riešenia rovnomerných rozvrhov, kde veľkosť aktivít pridelených zdrojom v danom čase je modelovaná pomocou náhodných premenných normálneho rozdelenia. Náhodné premenné sú zvolené namiesto reálnych čísel kvôli ich schopnosti zachytiť dostatočné množstvo informácie potrebnej na vytvorenie požadovaného optimálneho rozvrhu, ktorý je vhodný pre každú realizáciu náhodnej premennej. Problematiku rovnomerných rozvrhov vieme zovšeobecniť a matematicky formulovať pomocou problému rovnomernosti riadkových súčtov stĺpcovo permutovanej matice [3,4], ktorý v angličtine vystupuje pod názvom “Matrix Permutation Problem”.

Pre nás zaujímavou variantou je problematika dvojriadkovej matice, ktorej prvky modelujem pomocou náhodných premenných. Problematiku rovnomernosti riadkových súčtov stĺpcovo permutovanej stochastickej dvojriadkovej matice transformujeme na stochastickú úlohu o batohu a riešiť pomocou teórie stochastického programovania [2] zmenou na vhodný deterministický model bivalentného programovania.

Poďakovanie

áto práca vznikla s podporou grantovej agentúry VEGA vrámci riešenia projektu 1/0374/11 “Modelovanie a optimalizácia mobility a infraštruktúry v logistických sieťach”.

Literatúra

Graham, R.L., Lawler, E.L., Lenstra, J.K., Rinnooy Kan, A.H.G., Optimization and Appro- ximation in Deterministic Sequencing and Scheduling: A Survey, 1979
Kall, P., Wallace, S.W., Stochastic programming, ISBN 0471951080, 1994
Peško, Š., Optimalizácia NP-ťažkých dopravných rozvrhov, ŽU Žilina, Habilitačná práca, 2002
Peško, Š., The Matrix Permutation Problem in Interval Arithmetic, Journal of Information, Control and Management Systems, vol. 1, num. 1, 2006
Teória pravdepodobnosti, Internetový zdroj, http://www.graduate.sk/Handlers/ Download.ashx?Id=136
Sum of normally distributed random variables, From Wikipedia, the free encyclopedia, 2011
Normal distribution, From Wikipedia, the free encyclopedia, 2011

¹Turnus je denný pracovný cyklus, ktorý má byť odjazdený vodičom v danom dni a pozostáva z postupnosti trás. Trasa je súbor jázd a jazda pozostáva z príslušného času (miesta) odchodu a príchodu autobusu.

O časopise

Meta

RSS

Problém rovnomerných rozvrhov a stochastické programovanie

Napísať príspevok

Rubriky

Burza práce

Štúdijné materiály

Archív