High quality water level control in tank system based on hybrid control

23. Január, 2012, Autor článku: Osuský Jakub, Elektrotechnika
Ročník 5, číslo 1 Pridať príspevok

This paper presents hybrid control of nonlinear SISO system, modeled by several linear models, providing accurate approximation of real system. Presented control method ensures good control performance in whole operating range. Stability between operating points is ensured using Bialas theorem and for whole system using quadratic stability. Algorithm for smooth controller output by switching between local controllers is included. Approach is demonstrated in details on example of tank system.

I. Introduction

PID controller is a generic control loop feedback mechanism (controller) widely used in industrial control systems. Many PID tuning rules for tight control [1], [2], [3] and some for smooth control [4] were published. But conventional controllers like PID and many control methods are useful to control linear processes. In practice, most processes are nonlinear. If a process is a just little nonlinear, it can be treated as a linear process. If a process is severely nonlinear, it can be very difficult to control.

Nonlinear processes are usually control using any advanced control methods like robust control, adaptive control or model predictive control. Robust control can be applied if nonlinearity is not too big and often yields lower performance. Adaptive control is founded on complicated parameter estimation. MPC needs high accuracy nonlinear model so big modeling effort must be done. Simple way how to obtain good performance using linear models and, in this case PID controllers, is hybrid control [5].

The main drawback of linear models is the inherited property that they only provide accurate approximation of the nonlinearity when the plant operates close to the chosen linearization point. As the plant drifts away, accuracy of such an approximation deteriorates
quickly having negative impact on the performance of the controller.

Therefore, in this paper, instead of one linear model, several linear models will be used which will provide accurate approximation in whole operating range of the tank system. For each linear model local PID controller will be designed and stored in matrix of controllers. Based on process operating position, appropriate controller from matrix will be chosen. Algorithm for smooth controller output, by switching between local PID controllers, was derived. Stability between operating points can be checked using Bialas theorem or quadratic stability and result of hybrid control is partly compared with robust control.

II. Preliminaries and problem formulation

Consider tank system with input flow controlled by servo valve V1 and output flow controlled by servo valve V₂ (Fig. 1). Aim is to control water level in the tank using valve V₁ by variable opening of valve V₂.

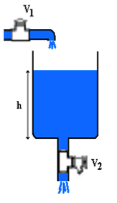
Fig. 1 Tank system with input and output flow

This tank system is typically nonlinear system because output flow rate depends not only on V2 opening but also on water level. According to Torricelli law the speed of a fluid flowing out of an opening is:

$v=\sqrt{2gh}$

(1)

To control the water level by different reference value, hybrid control will be used, where nonlinear process will be approximate be several linear models. Output valve opening changes dynamical properties of whole system which can cause lower performance or instability by robust control. From hybrid control point of view output valve opening means only several linear approximations more. Problem can be formulated as follows. Design hybrid control for water tank system with high performance which holds by reference and output opening change. Designed control has to provide stability of whole system and smooth local controllers switching.

III. Theoretical results

III.1. Reference control problem

For simplicity in first step consider tank system output valve fixed on any value for example 35%. Manipulating with valve V1 and measuring water level, it is possible to create static characteristic of tank system (fig. 2).

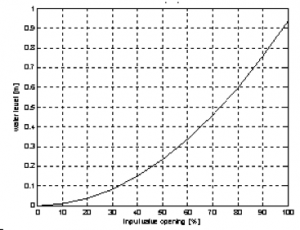
Fig. 2 Static characteristic of tank system, output valve 35%

Static characteristic is nonlinear and could be approximate using linear models (in our case four models, fig. 3).

Fig. 3 Static characteristic with linear models

These models are simple to obtain using input-output identification. For each model local PID controller can be tuned using any well known and tested method. Depending on water level, hybrid controller switches between designed local PID controllers. By controllers switching, controller output has to be smooth and stability of segment between operating points has to be ensured.

To obtain smooth controller output, by switching, weighting of local controllers outputs will be used. Consider switching water level h_sw, interval in which weighting will be done h_down < h_sw < h_up (for example boundaries could be ±5% of h_sw) and two local controllers in discrete form.

$R_1(z) = \frac{q_{01}+q_{11}z^{-1}+q_{21}z^{-2}}{1-z^{-1}}$

$R_2(z) = \frac{q_{02}+q_{12}z^{-1}+q_{22}z^{-2}}{1-z^{-1}}$

(2)

R₁ is local controller for model with lower water level and R₂ is local controller for model with higher water level. Local controllers’ outputs can be calculated as follows,

$\Delta u_1(k) = q_{01}e(k)+q_{11}e(k-1)+q_{21}e(k-2)$

$\Delta u_2(k) = q_{02}e(k)+q_{12}e(k-1)+q_{22}e(k-2)$

(3)

and final controller output is calculated using both local outputs and appropriate weight α.

$u(k) = u(k-1) + (1-\alpha)\Delta u_1(k)+ \alpha \Delta u_2(k)$

(4)

Where α depends on actual water level h and its calculated according (5).

$\alpha = \frac{h-h_{down}}{h_{up}-h_{down}}$

(5)

Switching between local controllers can cause system instability. So after controllers design, stability check is necessary. Stability analysis will be illustrated on simple example. Consider that in four operating points from fig. 3 input-output identification was done and transfer functions G₁(s),…,G₄(s) were obtained. For this transfer functions local PID controllers R₁(z),…,R₄(z) were designed. When the tank is empty R₁(z) is used for control and as the water level increased R₁(z) is switched to R₂(z), R₂(z) to R₃(z) and finally R₃(z) to R₄(z). So from stability point of view it is necessary to check only stability of segments ps₁, ps₂ and ps₃ (fig. 4).

Fig. 4 Operating points with segments

For segment stability analysis it is necessary to calculate p_i ,characteristic equation in i-th operating point (6).

$1+R_i(s)G_i(s) = 0$

(6)

Segment stability analysis will be done according Bialas theorem [6]: Characteristic equation of segment ps

$p(s,\chi) = \{ (1-\chi)p_1(s) + \chi p_2(s), \chi \in <0,1> \}$

(7)

is stable if and only if p₁(s) and p₂(s) are stable and Hurwitz matrix

$H_n = (H_n^{(1)})^{-1}H_n^{(2)}$

(8)

has positive eigen values.

$\lambda_i((H_n^{(1)})^{-1}H_n^{(2)}) \notin (-infty,0), \quad i=1,..,n$

(9)

If any segment is unstable, local controllers, in operating points of this segment, have to be tuned again. Usually controller tuning which increase phase margin helps to make segment stable.

III.2. Disturbance rejection problem

Opening and closing output valve V2 changes static and dynamic properties of tank system. Manipulating with this valve from minimum to maximum values it is possible to measure different static characteristics (fig 5).

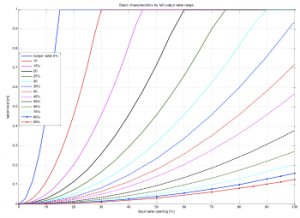
Fig. 5 Static characteristics for output valve 5-95%

Output valve changing is moving from one static characteristic to other one (disturbance rejection), whilst water level changing is moving up and down on the same static characteristic (reference tracking). Using hybrid control for each static characteristic several linear models will be obtained and hybrid controller will switch between local controllers according to output valve opening and water level.

Smooth controller output algorithm will changed, cause operating point can change in two dimensions (water level change, output valve change) and for stability analysis more segments has to be checked. Smooth control output algorithm has to consider now weighting of local controllers also by output valve change, fig. 6

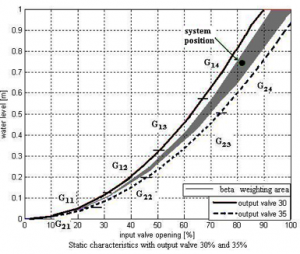
Fig. 6 Local controllers weighting due to output valve position

Algorithm will be almost same like by water level weighting. Consider output valve opening ov in weighting interval

$ov_{left} < ov < ov_{right}$

(10)

Local controllers R₁₄(z) and R₂₄(z) are the same type like (2). Also controller outputs ∆u₁₄(k) and ∆u₂₄(k) will be calculated like in (3). Final controller output is calculated using both local outputs and appropriate weight β.

$u(k) = u(k-1) + (1-\beta)\Delta u_{14}(k)+ \beta \Delta u_{24}(k)$

(11)

Where β depends on actual output valve opening ov and its calculated according

$\beta = \frac{ov-ov_{left}}{h_{right}-h_{left}}$

(12)

But in some cases three or four local controllers has to be considered. It is because system could have both output valve opening and also water level in weighting area, fig. 7.

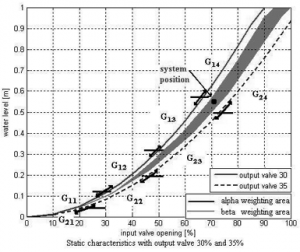
Fig. 7 Local controllers weighting due to water level and output valve position

In this case local controllers R₁₃(z), R₁₄(z), R₂₃(z) and R₂₄(z) for transfer functions G₁₃(s), G₁₄(s), G₂₃(s) and G₂₄(s) are considered. Final controller output is calculated as combination of (11) and (4).

$u(k) = u(k-1) + (1-\beta)[ (1-\alpha_1) \Delta u_{13}(k) + \alpha_1 \Delta u_{14}(k)]+$

$\beta [(1-\alpha_2) \Delta u_{23}(k) + \alpha_2 \Delta u_{24}(k)]$

(13)

α₁ is weight depending on water level weighting interval for full line static characteristic and α₂ is weight depending on water level weighting interval for dashed one (fig. 7).

Stability analysis contains more segments, cause for example, from local transfer function model G₂₃(s) is possible to move by output valve closing to G₁₃(s) (higher water level) but also to G₁₂(s) (lower water level). For example on figure 6, thirteen segments has to be tested fig. 8

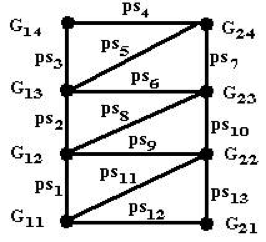
Fig. 8 Segments for two static characteristics

Stability of whole system with controller can be confirmed also using quadratic stability. System is stable if there is a real symmetric positive definite matrix P satisfying the following Lyapunov matrix inequality

$A_i^T P + P A_i < 0, \quad i=1,..,n[/latex]</td> <td style="width:20px; text-align:center;">(14)</td> </tr> </table> Where n is number of indentified linear models, and A_i is a closed loop state space matrix of i-th identified linear model with local controller. IV. Case study For tank system, static characteristics were measured by different output valve opening fig. 5. Each static characteristic was approximate by three or four linear models. Parameters of 51 linear models were obtained from genetic algorithm based on input-output measurements. The genetic algorithm is based on consecutive production of various solutions for a given problem. During the process run, socalled population is kept. This population consists of terms and each term is one solution of given problem. As the population goes through the evolution, the solutions get better. Using genetic algorithms, the values of transfer functions parameters were determined. These values are much more precise than the values determined by ARX model and it is closer to the currently used value. More about genetic algorithm [7]. Example of real system and model matching, in operating point 3, by 35% output valve opening, fig. 9. <a href="http://www.posterus.sk/wp-content/uploads/p12560_09_obr09.png"><img src="http://www.posterus.sk/wp-content/uploads/p12560_09_obr09-300x260.png" alt="" title="p12560_09_obr09" width="300" height="260" class="alignright size-medium wp-image-12571" /></a> Fig. 9 Comparison of model and real system Approximation of nonlinear characteristic example (output valve 35%) using linear models is depicted in figure 10. Similar accuracy was reached also by approximation of others static characteristics. <a href="http://www.posterus.sk/wp-content/uploads/p12560_10_obr10.png"><img src="http://www.posterus.sk/wp-content/uploads/p12560_10_obr10-300x229.png" alt="" title="p12560_10_obr10" width="300" height="229" class="alignright size-medium wp-image-12572" /></a> Fig. 10 Example of static characteristic approximation For local controller tuning several well known methods was tried [3, 4, 8, 9] but all methods provided solution with overshoot or with very long settling time. Therefore for each model local controller was designed using genetic algorithm. Aim of controller design was reference tracking without overshoot. Genetic algorithm was able to find the best parameters of PID controller, which represents the best closed loop control. The length of a string depends on controller type. PID controller is defined by three parameters, therefore the string has three parameters (genes) which represent P, I and D item. The range of each parameter as an interval (searched space) was set as <0 , 10> for P, <0 , 10> for I and <0 , 1> for D. Population has only 30 strings, due to the fact that only 3 parameters were looked for. Quality of solution was determined as fitness what is sum of absolute values of difference between set point and system output. For controller tuning needs set point was set as a few steps around the mean value of each linear segment. The condition of minimal overshoot was fulfilled by the penalizing of solutions with overshoot. Each sample of system output which is over the set point (step to higher value) is multiplied by number 100 and this value is included in fitness value. This way is preferred solutions without overshoot. For PID parameters evaluation, antiwindup structure with controller output rate limiter was used. Rate limiter was set on <0.03;-0.03> per second because servo valve V1 on tank process needs 10s to open from minimum (0[l/s]) to maximum value (0.3 [l/s]). Genetic algorithm was run in cycle 51 times, once for each identified linear model. Parameters for all 51 PID controllers were calculated in one hour (IP D 2Core 3.0 GHz). <a href="http://www.posterus.sk/wp-content/uploads/p12560_11_obr11.png"><img src="http://www.posterus.sk/wp-content/uploads/p12560_11_obr11-300x237.png" alt="" title="p12560_11_obr11" width="300" height="237" class="alignright size-medium wp-image-12573" /></a> Fig. 11 Segments of whole system According to fig. 11 more than hundred segments were checked to proof the stability of system with hybrid control, according (9). Stability of whole system was proofed also using quadratic stability where following real symmetric positive definite matrix P satisfying inequality (14) was found using yalmip toolbox [10]. <table style="width:100%;"> <tr> <td style="text-align:center;"><img src='http://s0.wp.com/latex.php?latex&bg=ffffff&fg=000000&s=0' alt='' title='' class='latex' />P = \left[ \begin{array}{ccc} 5.1 & 22.8 & 34.5 \\ 22.8 & 1603.6 & 2779 \\ 34.5 & 2779 & 8093.6 \end{array} \right ]$

(15)

When controllers were designed comparison of sharp local controllers switching and smooth controllers switching was done fig. 12.

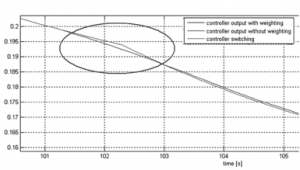
Fig. 12 Smooth and sharp controller switching

In fig. 12 controllers switch was done in 102.3s. It is possible to see that using controller output with weighting, smoother response was obtained, like using sharp controller switching. Using hybrid control step responses with similar performance should be obtianed independently on water level or output valve opening. Few step changes were done for each output valve openenig value fig. 13, 14.

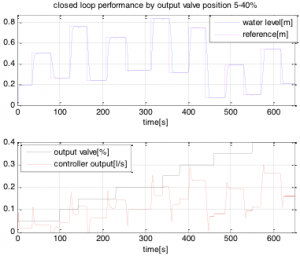
Fig. 13 Step responses for output valve openenig 5-40%

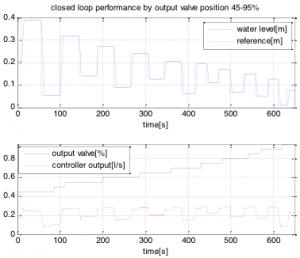
Fig. 14 Step responses for output valve openenig 45-95%

Output valve opening is disturbance from control point of view. Local controllers were tuned for good reference tracking (without overshoot), but are also fast enough for excelent disturbance rejection (Fig. 13, 14). Using robust control depends on uncertainty. If the uncertainty is too big robust approach can’t be used. For comparison of robust and hybrid control, robust control approach described in (Osusky, Vesely 2011) was used. Using all identified models it was not possible to design robust controller, due to big uncertainty.

By considering two static characteristic (30%, 35% output valve opening) from figure 5, it is possible to compare robust control with hybrid control. Robust controller was designed for nominal model and robust condition was verified. But nominal model does not fit the real system so good as eight linear models by hybrid control. Robust controller ensures overshoot approximately 3% (fig. 15) but only for nominal model. Comparison of hybrid and robust control is depicted in fig. 16. (Black line shows valve opening and closing). Fig. 17 compares controller outputs and show how the hybrid controller switch between local controllers from table in appendix B, rows 30% and 35%. Robust controller parameters:

$R_{robust}(s) = \frac{0.528s+0.25}{s}$

(16)

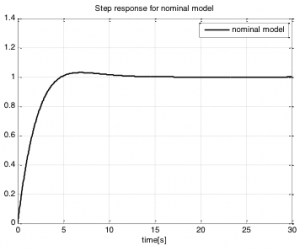
Fig. 15 Nominal model step response, robust controller

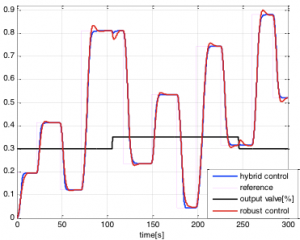
Fig. 16 Robust and hybrid control comparison

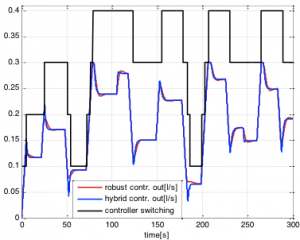
Fig. 17 Robust and hybrid controller output comparison and controller switching line

In fig.16 is it possible to see that overshoot using robust controller is changing dependently on water level and output valve opening due to system nonlinearity. Settling time using hybrid control is shorter as using robust control. System is without overshoot using hybrid control by all step changes, but using robust control it is in range (0-3.62)%. Disturbance rejection is also much better using hybrid control (time 105s, 245s )

V. Conclusion

In this paper hybrid control of water tank system was presented. Stability of system with hybrid control was confirmed using Bialas stability theorem and also quadratic stability. Algorithm for smooth controller switching, by water level change and output valve opening, was derived. Presented hybrid control was compared with robust control by output valve in 30 and 35%%. In this paper as ‘real’ system, nonlinear model of real tank system was considered. Aim of the future work is implementation of presented hybrid control into PLC which controls the real tank system situated in lab.

Acknowledgements

This work was supported by the Scientific Grant APVV 0211-10

References

K. J. Astrom, T. Hagglund,. PID Controllers: Theory, Design and Tuning. 2nd Edn., ISA Pub., North Carolina, 1995.
J. B. Ziegler and N. B. Nichols, Optimum settings for automatic controllers,, ASME Transactions, v64 , pp. 759-768, 1942
S. Skogestad, Simple analytic rules for model reduction and PID controller tuning. Journal of Process Control 13,, 2003.
S. Skogestad, Tuning for smooth PID control with acceptable disturbance rejection”, Ind.Eng.Chem.Res, 45 (23), 7817-7822, 2006.
M. Kvasnica., M. Herceg, L. Čirka, M. Fikar, Model predictive control of a CSTR: A hybrid modeling approach, Springer’s Journal No. 11696, ISSN: 1336-9075, 2009
S. Bialas, A necessary and sufficient condition for the stability of convex combinations of stable polynomials or matrices. Bull. Polish Acad.Sci., Tech. Sci. 33 (9-10), 473-480, 1985
M. Oravec, Števo, S., Sekaj, I. Comparison of using simple genetic algorithm and parallel genetic algorithm in heat transfer model optimization, Journal of Cybernetics and Informatics, vol. 9, ISSN: 1336-4774, 2010
J. Osuský, V. Veselý.: Modification of Neimark D-partition method for desiredphase margin, International Conference Cybernetics and Informatics, February 10 – 13, 2010, VYŠNÁ BOCA, Slovak Republic,
H. W. Fung, Q.G. Wang, T.H. Lee (1998): PI Tuning in terms of gain and phase margins, Automatica, 34, pp. 1145-1149
J. Lofberg. YALMIP: A toolbox for modeling and optimization in MATLAB,IEEE International Symposium on Computer Aided Control Systems Design, Taipei, Taiwan, 2004

Co author of this paper is Ing. Stanislav Števo, PhD.

O časopise

Meta

RSS

High quality water level control in tank system based on hybrid control

Napísať príspevok

Rubriky

Burza práce

Štúdijné materiály

Archív