This article describes computational fluid dynamics (CFD) analysis of cooling processes of electrical Cu conductor with PVC insulation. Horizontally conductor was loaded by electric current and its cooling process was caused by influence of free convection of air and radiation. Results of CFD analysis were compared with experimental results.

1. Introduction

Cables with PVC based insulation blends are nowadays still one of the most applied types of cables in eastern and central Europe. Use of this material in power engineering is widespread especially due to its acceptable mechanical and electrical properties and its available price. After decades of operation we experience various malfunctions of these systems caused by degradation, especially effects of thermal ageing. According to Arrhenius law, the rate of chemical reactions – the rate of degradation – increases exponentially with increasing thermodynamic temperature. It means, the lifetime of insulation decreases exponentially with increasing temperature.

Therefore, the maximum continuous operating performance and current loading capacity of cables and wires is important criterion in the design of cable systems (insulation materials, construction) and design of power electrical installation (e.g. deposit method). Primarily, the passing electrical current by means of Joule losses heats up the conductor and therefore its temperature and temperature of its electrical insulation system exceeds the ambient temperature. This temperature depends quadratically on the passing current. Long-term exceeding of projected operating temperatures of cable conductors causes significantly faster ageing of insulation, increases corrosion of cable cores in extreme cases and deterioration of mechanical properties of insulation.

In recent years, there has been rapid development of computational methods, models and simulations, which allow determining the steady state temperature of the current passing insulated conductor. In this paper computational fluid dynamics (CFD) analysis was used to simulate cooling process of horizontally electric copper conductor (thermal conductivity 401 Wm^-1K^-1) with diameter of 1.48 mm, insulated with PVC insulation blend 0.81 mm thick (thermal conductivity was set to 0.14 [1]). The conductor carried AC current according to measurement order from 5 to 30 A RMS. Cooling of the conductor was only due to free convection and radiation effects (ambient temperature was 22 °C). CFD analysis results of surface temperatures on the Cu core and on PVC insulation surface under steady thermal-electric state were compared to the measurement temperatures.

2. CFD analysis

CFD is a branch of fluid mechanics that uses numerical methods and algorithms to solve and analyze problems that involve fluid flows. Computers are used to perform the calculations required to simulate the interaction of liquids and gases with surfaces defined by boundary conditions. CFD analysis of cooling the conductor was performed in software ANSYS CFX [2]. Geometry for the model:

• air area around the conductor: block with dimensions 2000×3000×1 mm (this area represents room with the conductor, thickness 1 mm is due to symmetry boundary condition mentioned below),
• conductor geometry: Cu core is represented by cylinder with diameter 1.48 mm and PVC insulation is ring with inner diameter 1.48 mm and outer diameter 3.1 mm, both have length 1 mm,
• position of conductor: a = 1100 mm, see Fig. 1.

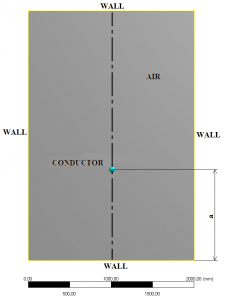
Fig. 1. Conductor position in the air area

We need to create mesh of volume elements in the air area. The mesh around the conductor surface and walls must be very fine (called inflation) because of near-wall boundary flow has to be modeled, see Fig. 2. Meshes for solid parts were also created. Final number of elements was 188 446.

Fig. 2. Mesh for CFX model

Boundaries of the air area were set as adiabatic walls. Air properties were chosen according to ANSYS CFX material library. The model was set up to solve free convection (ambient temperature 22°C). Radiation effect considered emissivity for yellow-green PVC insulation ε = 0.62 [3].

The body of conductor itself was modeled also. Joule heat generation due to electric current was considered in Cu core. The reason why the thickness of the model is only 1 mm is that there are symmetry conditions on the front and back surface of the model. That means the model itself represents infinite region in this direction (infinite length of the conductor). Results of analysis were surface temperatures of the Cu core and PVC insulation. The simulation was calculated as steady-state analysis using cluster computer 16 × 4.4 GHz cores, 64 GB of RAM. Iterative solution took approximately 10 hours for every load step (number of iterations approx. 15 000).

Cooling of conductor by free convection is shown in Fig. 3. Fig. 4 shows inconstant values of convective heat transfer coefficient on conductor surface calculated in CFX for loading current 25 A. Final surface temperature of the conductor was obtained as average temperature on the conductor surface, see Fig. 5. But this average temperature is not constant value during fictive iteration time (real behavior of air flow around conductor is oscillating transient stream, called von Kármán stream [4, 5]), therefore the average temperature was obtained according to chosen number of iterations at the end of simulation, see Fig. 6. Final results of surface temperatures are in Table 1.

Fig. 3. Air temperature around conductor (left) and air velocity (right) – ANSYS CFX

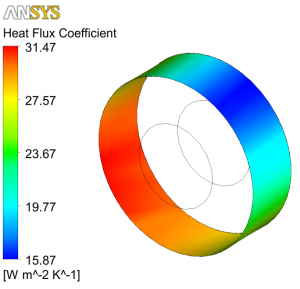
Fig. 4. Convective heat transfer coefficient (loading current 25 A)

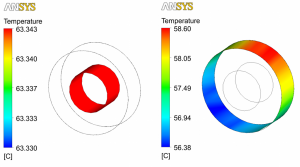
Fig. 5. Temperature (loading current 25 A) – surface of Cu core (left) and outer surface of PVC insulation (right)

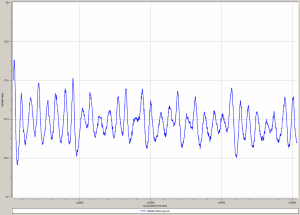
Fig. 6. Temperature changes on conductor surface during iterative process

Tab. 1. Surface temperatures – CFX simulation

I [A] t_{CFX Cu} [°C] t_{CFX PVC min} [°C] t_{CFX PVC max} [°C] t_{CFX PVC ave} [°C] 5 24.18 23.90 24.01 23.96 10 29.40 28.36 28.69 28.52 15 37.44 35.22 35.87 35.47 20 48.77 44.59 45.86 45.04 25 63.34 56.38 58.60 57.28 30 81.06 70.60 74.01 71.85

3. Experimental mesurement

The experimental results proposed in this paper were achieved by loading characteristic measurements for horizontal Cu conductor, diameter 1.48 mm, with PVC blend insulation, 0.81 mm thick. Current in the measurement circuit (5, 10, 15, 20, 25 and 30 Amps AC) was regulated by autotransformer (AT) and current transformer (PT) (see Fig. 7 for connection details) and measured by analog ammeter (A) (precision 0.5 %).

Conductor surface temperatures under insulation and on the PVC insulation surface were measured by K-type thermocouple and real time logged into computer by Fluke 289 multimeter (MT) and support logging software Fluke View Forms (PC), see Fig. 8. Time logging interval was set to 5 seconds. Temperature measurement precision was 0.5%. Ambient temperature during measurement was 22 °C. Results from measurement are in Tab. 2.

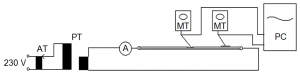
Fig. 7. Schematic illustration of the experimental setup.

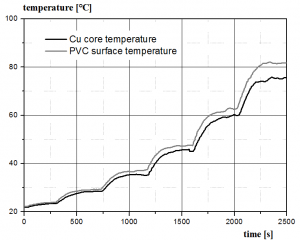
Fig. 8. Time evolution of conductor temperature and insulation surface temperature (loading currents: 5, 10, 15, 20, 25, 30 A)

Tab. 2. Surface temperatures – experimental measurement

I [A] t_{measure Cu} [°C] t_{measure PVC} [°C] 5 23.9 23.5 10 29.3 28.5 15 37.4 36.1 20 47.5 45.8 25 62.6 60.0 30 80.1 75.2

4. Comparison and conclusion

CFD analysis considers effect of air flow around the conductor. Air is heated due to Joule losses caused by passing electric current and therefore air flows around conductor with different velocities and causes different heat drain around the conductor surface (inconstant convective heat transfer coefficient). This fact is reason that CFD results correspond quite well in comparison with experimental measurement. Fig. 9 and 10 show calculated and measured surface temperatures of conductor in graphic form. In Tab. 3 there are differences of temperature for CFD simulation in comparison to measurement.

CFD disadvantage is hardware- and time-intensiveness. But CFD great advantage is its automatic calculation of convective heat transfer coefficient, which calculation is problematic for complicated solid geometry.

Tab. 3. Differences of Cu core and PVC insulation surface temperatures

I [A] t_{measure Cu} [°C] Δt_{CFX Cu} [%] t_{measure PVC} [°C] Δt_{CFX PVC ave} [%] 5 23.9 -1.17 23.5 -1.96 10 29.3 -0.34 28.5 -0.07 15 37.4 -0.11 36.1 1.75 20 47.5 -2.67 45.8 1.66 25 62.6 -1.18 60.0 4.53 30 80.1 -1.20 75.2 4.45

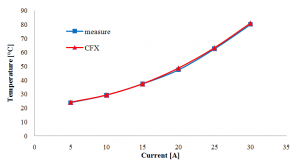
Fig. 9. Graph of Cu core surface temperatures

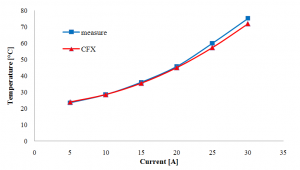
Fig. 10. Graph of PVC surface temperatures

Acknowledgements

This contribution is the result of the project implementation: Completion of the National center for research and application of renewable energy sources (ITMS: 26240120028), supported by the Research & Development Operational Programme funded by the ERDF. This work was supported by Grant Agency KEGA, grant No. 015STU-4/2012 and grant VEGA 1/0534/12.

References

1. MATBASE a leap forward in material data, available online:
   http://www.matbase.com/material/polymers/commodity/soft-pvc/properties
2. ANSYS CFX, Theory manual, 2011
3. Zhu, S., Deltour, J., Wang, S.: Modeling the thermal characteristics of greenhouse pond systems, Aquacultural Engineering, vol. 18, pp. 201-217, 1998
4. The influence of heat on the 3D-transition of the von Kármán vortex street International Journal of Heat and Mass Transfer, Volume 46, Issue 16, July 2003, Pages 3069-3081, W.J.P.M. Maas, C.C.M. Rindt, A.A. van Steenhoven
5. Heat transfer from a line source located in the periodic laminar near wake of a circular cylinder, Experimental Thermal and Fluid Science, Volume 29, Issue 8, September 2005, Pages 947-956, G. Godard, F. Weiss, M. Gonzalez, P. Paranthoën

---

Co author of this paper are Juraj Paulech, Michal Váry