What is mechanical vibration and why its understanding is important for mechanical and civil engineers? Let`s look to history. On 1st July 1940 Tacoma Narrows Bridge was opened to traffic and in the morning on 7th November of the same year the bridge`s main span collapsed under wind conditions. This event is presented as an example of elementary forced resonance with the wind providing an external periodic frequency that matched the bridge`s natural structural frequency, though the actual cause of failure was aeroelastic flutter.

Wind as external force affects a twisting oscillation of bridge (Fig.1). This force with specific frequency caused a resonance disaster of bridge (wind speed was mild 64 km/h) [1]. Other example of resonance disasters is collapse of Broughton Suspension Bridge due to soldiers walking in step [3].

Fig. 1 Collapse of Tacoma Narrows Bridge [2].

In mechanics and construction a resonance disaster describes the destruction of a building or a technical mechanism by induced vibrations at a system’s resonance frequency, which causes it to oscillate. Periodic excitation optimally transfers to the system the energy of the vibration and stores it there. Because of this repeated and additional energy input the system swings ever more strongly, until its load limit is exceeded [4].

Common cause of mentioned disasters was periodic oscillations of the bridges. Periodic oscillation can be described as motion of body which regularly passes the equilibrium position. Any oscillation motion of mechanical system about its equilibrium position is called vibration [5]. The simplest example of vibration system is mass-spring system (Fig. 2). Body represents by a mass starts vibrate when it is displaced from a position of stable equilibrium. Body keep moving back and forth across its equilibrium caused by restoring force, in this case restoring forces is elastic force of spring. This elementary vibration system is called mechanical oscillator.

Mass-spring system performs harmonic periodic motion with constant amplitude of displacement if the system is undamped. Undamped system conserves mechanical energy – harmonic motion will carry on vibrating forever. There will be continues interchange of kinetic to potential energy and back again. But undamped system is simplifying of reality because in the real world is impossible to isolate the system – friction and air-resistance drains mechanical energy from system into environment in form of heat energy. Total mechanical energy left in the system therefore gradually decreases – amplitude of displacement also decreases in time (Fig. 3). [6]

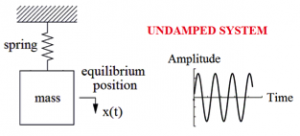
Fig. 2 Undamped mechanical oscillator.

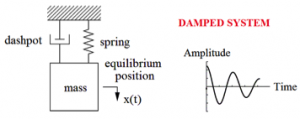
Fig. 3 Damped mechanical oscillator.

Other elementary mechanical oscillators are shown on Fig. 4:

• simple pendulum: restoring force is gravitational force (Fig. 4a),
• bending beam: restoring force is elasticity of beam material (Fig. 4b),
• torsion of shaft: restoring force is elasticity of shaft material (Fig. 4c).

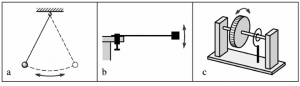
Fig. 4 Mechanical oscillators.

Almost every machines produce vibrations, for example combustion engines vibrate caused by periodic movement of pistons, rotational devices vibrate caused unbalanced parts; automobiles vibrate caused by road surface roughness, etc. Human speech is a product of vocal cord vibration, recognize sounds is caused by oscillation of the eardrum, operation of many musical instruments is based on vibration (guitar string vibration, Fig. 5).

Alternative current (AC) is the result of periodic oscillations of electric charges. If AC flows through induction coil the magnetic field in coil’s cavity is changed. AC also changes electric field in electrical capacitor. These examples show that vibration is not phenomenon only in mechanical engineering but it is an element in many other physical domains (electricity, magnetism, etc).

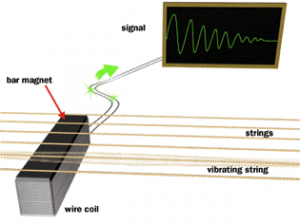
Fig. 5 Guitar string vibration [7].

Vibrations can be classified into three categories:

• Free vibration [8] of a system is vibration that occurs in the absence of external force. The sources of free vibration are initial displacement of system from equilibrium or give the initial velocity to the system.

  
  Fig. 6 Free vibration: string vibration [9].

• Forced vibration [8] is caused by an external force that acts on the system. In this case, the exciting force continuously supplies energy to the system.

  
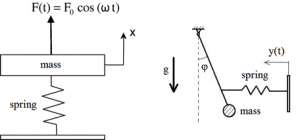
  Fig. 7 Forced vibration: system forced by a harmonic external force (left), system forced by a time-dependent displacement (right).

• Self-excited vibration [10] is periodic and deterministic oscillation. Under certain conditions, the equilibrium state in such a vibration system becomes unstable, and any disturbance causes the perturbations to grow until some effect limits any further growth. In contrast to forced vibrations, the exciting force is independent of the vibrations and can still persist even when the system is prevented from vibrating. The force acting on a vibrating object is usually external to the system and independent of the motion. However, there are systems in which the exciting force is a function of the motion variables (displacement, velocity or acceleration) and thus varies with the motion it produces. Friction-induced vibration (in vehicle clutches and brakes, vehicle-bridge interaction) and flow-induced vibration (circular wood saws, CDs, DVDs, in machining, fluid-conveying pipelines), fluttering of airplane wing (Fig. 9) are examples of self-excited vibration

  
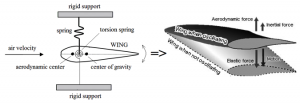
  Fig. 8 Self-excited vibrations: fluttering of wing [10, 11].

Most vibrations are undesirable in mechanical engineering. Vibrations in machines and structures because produce increased stresses, energy losses, cause added wear, increase bearing loads, induce fatigue, create passenger discomfort in vehicles, and absorb energy from the system [8]. Rotating machine parts need careful balancing in order to prevent damage from vibrations [8]. The worst impact has resonance of mechanical systems. Resonance can occur when forced vibration and can cause even at low loads serious damages. Understanding of vibrations is therefore very important for engineers.

Mechanical systems is general consist of structural components which have distributed mass and elasticity. Examples of these structural components are rods, beams, plates, and shells. These structural components are considered as continuum systems which have an infinite number of degrees of freedom (DOF) and therefore the vibration of real systems is governed by partial differential equations which involve variables that depend on time as well as the spatial coordinates. For study of vibration is preferred by simplifying real system to discrete system with a finite number of DOF. Discrete system is represented by lumped mass and discrete elastic elements (translational and torsion springs) and discrete damped elements (viscous dashpots). Physical models of discrete systems are shown in Fig. 2, 3 and 7. These systems are governed by a set of second-order ordinary differential equations. [12]

The cantilever beam is an example of a continuum system. Under certain conditions this beam can be modeled as a simple discrete spring-mass system. In order to model the vibration of the cantilever beam, the end of the beam is chosen as a reference point at which the characteristics and response of the beam are measured (Fig. 9). An equivalent system is then built that has a response – y(t), that is identical to that of the actual system.

The spring constant – k, of the equivalent system is identical to that of the cantilever beam, and can be calculated quite easily using beam deflection formulae. Calculation of an equivalent mass is necessary because all points along the beam’s length do not have the same response as the end of the beam. This means that the equivalent mass – m, cannot be determined simply by adding the masses m_beam and m_end, but must be found by equating the energies of the two systems as they vibrate (this type of analysis is called lumping). [13]

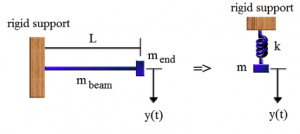
Fig. 9 Cantilever beam as a simple spring-mass system [11].

Basic information about mechanical vibrations was described. In next chapters the vibration motion will be analyzed. We will concentrate to free and forced vibrations of damped and undamped discrete systems.

References

1. http://en.wikipedia.org/wiki/Tacoma_Narrows_Bridge_%281940%29
2. http://www.youtube.com/watch?v=j-zczJXSxnw
3. http://en.wikipedia.org/wiki/Mechanical_resonance
4. http://en.wikipedia.org/wiki/Resonance_disaster#Resonance_disaster
5. Krodkiewski, J., M.: MECHANICAL VIBRATION, The University of Melbourne, 2008
6. http://www.cyberphysics.co.uk/topics/shm/damping.htm
7. http://entertainment.howstuffworks.com/electric-guitar1.htm
8. Dukkipati, R.V.: SOLVING VIBRATION ANALYSIS PROBLEMS USING MATLAB, 2007, ISBN 978-81-224-2064-7
9. http://www.home.agilent.com/agilent/editorial.jspx?ckey=866697&id=866697&lc=eng&cc=AW
10. www.liv.ac.uk/~mehou/Y3_AERO/AeroL40.doc
11. http://www.apg.jaxa.jp/eng/publication/ap_news/2011_no21/apn2011no21_03.html
12. Shabana, A.: VIBRATION OF DISCRETE AND CONTINUOUS SYSTEMS, Springer, 1996
13. http://www.lcs.syr.edu/faculty/glauser/mae415/vibesLab/goodVibesExp.html