Mapping of the neutron flux density distribution in the VVER-440 reactor pressure vessel

12. August, 2009, Autor článku: Stacho Matúš, Elektrotechnika, Študentské práce
Ročník 2, číslo 8 This page as PDF Pridať príspevok

One of the limiting factors in term of nuclear power plant lifetime is reactor pressure vessel (RPV) condition. The most important ageing effect on the RPV is embrittlement. Its radiation embrittlement cause especially fast neutrons. In this work we are focused on describing neutron field in RPV area of reactor VVER-440/V-213 using simulation code MCNP 5. The goal of this work is to improve the assessment of the reactor RPV degradation and following valuation possibility of its lifetime extension and comparison of neutron flux and neutron spectra in most loaded place of RPV and surveillance specimen area.

Introduction

The structural materials in reactor are damaged by radiation, which comes from fission reaction. Gamma rays can create only close Frenkel pairs. Neutrons, especially the fast ones, can knock on primary atoms, which can obtain such energy, that they could knock on set of secondary atoms from the structural lattice. These defects can diffuse and create bigger defects, which leads to embrittlement of structural materials. [1] Therefore we are interested in neutron fluence in reactor pressure vessel. MCNP code is a statistic code, which can compute neutron flux density and time integral of neutron flux density is equal to neutron fluence.


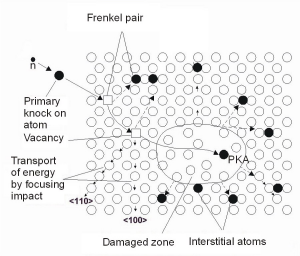
Fig. 1 Scheme of neutron damage

Simulation description

Mapping of the neutron flux density distribution in RPV has been realized for full-core model of VVER-440/V213. Fig. 2 and 3 depict axial and radial view of model. The core contains all types of fuel and control assemblies currently used in Slovak nuclear power plants. These are fuel assemblies from previous supply (3.82%) and the second generation fuel, designated also as the Gd-2 (4.25%). Fuel composition corresponds to average burn-up level of 26000 MWd/tHM. It is identical for each assembly type. Boric acid concentration of 3.4 g/kg and position of the sixth group of control assemblies of 195 cm were set in the input. Details of the model in RPV area show Fig. 4.


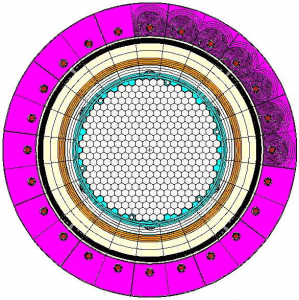
Fig. 2 Axial view of the model


Fig. 3 Azimuthal view of the model


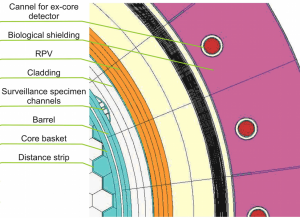
Fig. 4 Detail of model in RPV area

KCODE (criticality calculation) was performed to obtain spatial neutron flux density distribution in the reactor. 30 000 neutrons per cycle in 100 inactive and 500 active cycles were set as input parameters. Improvement of statistical parameters was reached by adjusting cell importance.

The model has been created according to reactor and core loading in sixth symmetry, therefore the mapping has been focused at one sixth of pressure vessel. The mapping has been realized by fmesh tally. The sixth of pressure vessel has been divided, by this mesh, in ten layers radially, twelve parts by five degrees azimuthally and in twenty levels by 12.8 cm axially.

The spectrum of neutron flux has been computed in two levels and three structural parts. Those three parts are irradiation channel for surveillance specimen, austenitic cladding of RPV and RPV and two levels correspond to fourth weld area and most loaded part in RPV.

Main results

The simulation results of neutron flux are normalized to one source neutron. The real neutron density is a time-integral of conjunction of computed neutron flux and source emisivity. The source emisivity could be obtained from power condition. Fig. 4 and 5 depict example of neutron flux distribution maps. Black box represents the fourth weld area.


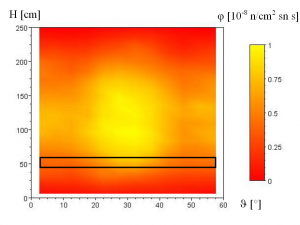
Fig. 5 Map of neutron flux density in first layer


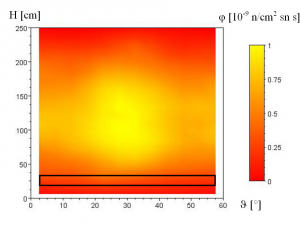
Fig. 6 Map of neutron flux density in last layer

The most loaded area (yellow) is in the average height of reactor core and azimuthal direction 30 degree. Tab. 1 and Fig. 7 depict radial dependence of neutron flux density in middle of reactor pressure vessel. The first two radial layers represent austenitic and power cladding RPV.

R [cm] \varphi‘ [n/cm2 sn s] \bigtriangleup_{\varphi} [n/cm2 sn s] R [cm] \varphi‘ [n/cm2 sn s] \bigtriangleup_{\varphi} [n/cm2 sn s]
177,525 7,29E-09 4,27E-10 184,125 2,20E-09 1,32E-10
177,975 6,33E-09 3,75E-10 185,875 1,75E-09 1,03E-10
178,875 5,15E-09 3,09E-10 187,625 1,37E-09 7,92E-11
180,625 3,63E-09 2,22E-10 189,375 1,02E-09 5,82E-11
182,375 2,77E-09 1,69E-10 191,125 6,74E-10 3,81E-11

Tab. 1 Results of radial neutron flux density dependence


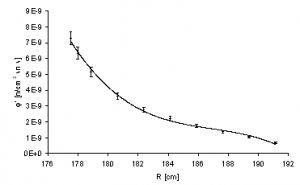
Fig. 7 Radial neutron flux density dependence

Tab. 2 and fig. 8 depict axially neutron flux density dependence in the middle of the pressure vessel first layer. The obtained dependences correspond to theoretical characteristics of homogenous reactor. The maximum is moved by influence of control assemblies to lower values.

H [cm] \varphi‘ [n/cm2 sn s] \bigtriangleup_{\varphi} [n/cm2 sn s] H [cm] \varphi‘ [n/cm2 sn s] \bigtriangleup_{\varphi} [n/cm2 sn s]
6,4 1,47E-09 1,80E-10 134,4 6,96E-09 3,86E-10
19,2 2,72E-09 2,52E-10 147,2 6,79E-09 4,14E-10
32 3,89E-09 2,86E-10 160 5,67E-09 3,48E-10
44,8 4,92E-09 3,28E-10 172,8 4,62E-09 3,18E-10
57,6 5,71E-09 3,31E-10 185,6 4,04E-09 2,93E-10
70,4 6,50E-09 3,46E-10 198,4 3,52E-09 2,74E-10
83,2 7,29E-09 4,01E-10 211,2 2,70E-09 2,13E-10
96 7,66E-09 4,39E-10 224 2,07E-09 1,82E-10
108,8 7,32E-09 3,92E-10 236,8 1,58E-09 1,77E-10
121,6 7,29E-09 4,27E-10 249,6 8,83E-10 1,45E-10

Tab. 2 Results of axial neutron flux density dependence


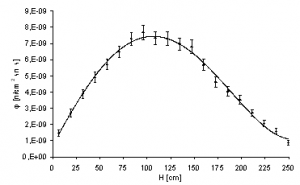
Fig. 8 Axial neutron flux density dependence

Spectrum of neutron flux density was computed in direction corresponding to the most loaded area of RPV and the most loaded area of fourth weld.
In the table 3 are simulations results from RPV, austenitic cladding (AC) and irradiation channel for surveillance specimen (ICh) for direction corresponding to the most loaded area of RPV. The Fig. 9 shows this spectrum. Fig. 10 show the spectrum normalized to maximum value, for better comparison.

E [MeV] \frac{\varphi^{\prime} }{\bigtriangleup E} [n/cm2 sn s MeV] \varphi^{\prime}_{n} [-]
RPV ICh AC RPV ICh AC
0,1 5,27E-09 2,36E-07 9,12E-09 1,00E+00 1,00E+00 1,00E+00
0,35 5,84E-10 1,38E-08 4,96E-10 1,11E-01 5,84E-02 5,44E-02
0,75 3,65E-10 8,31E-09 3,25E-10 6,91E-02 3,52E-02 3,56E-02
1,75 1,20E-10 3,25E-09 1,20E-10 2,27E-02 1,38E-02 1,32E-02
6,25 8,90E-12 2,05E-10 1,04E-11 1,69E-03 8,69E-04 1,14E-03

Tab. 3 Results of energy dependence of neutron flux density in direction corresponding to the most loaded area


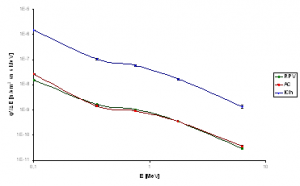
Fig. 9 Spectrum of neutron flux density φ’ in the middle of RPV


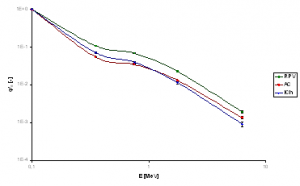
Fig. 10 Spectrum of normalized neutron flux density φ’n in the middle of RPV

In the table 4 are simulations results from RPV, austenitic cladding (AC) and irradiation channel for surveillance specimen (ICh) for direction corresponding to the most loaded area of fourth weld of RPV. The Fig. 11 shows this spectrum and Fig. 12 show the spectrum normalized to maximum value.

E [MeV] \frac{\varphi^{\prime}}{\bigtriangleup E} [n/cm2 sn s MeV] \varphi^{\prime}_{n} [-]
RPV ICh AC RPV ICh AC
0,1 1,54E-08 1,49E-06 2,66E-08 1,00E+00 1,00E+00 1,00E+00
0,35 1,67E-09 1,06E-07 1,44E-09 1,08E-01 7,10E-02 5,42E-02
0,75 1,07E-09 5,95E-08 9,18E-10 6,91E-02 3,98E-02 3,46E-02
1,75 3,49E-10 1,70E-08 3,48E-10 2,26E-02 1,14E-02 1,31E-02
6,25 2,97E-11 1,37E-09 3,59E-11 1,93E-03 9,14E-04 1,35E-03

Tab. 4 Results of energy dependence of neutron flux density in fourth weld area


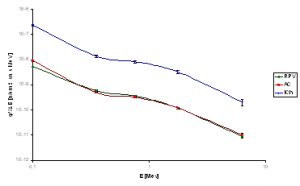
Fig. 11 Spectrum of neutron flux density φ’ in fourth weld area level


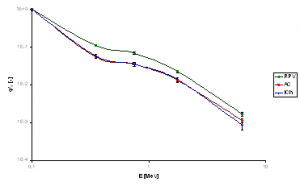
Fig. 12 Spectrum of normalized neutron flux density φ’n in fourth weld area level

Conclusion

The complex model of reactor VVER-440/V213 has been developed. Simplified neutron flux density mapping has performed using mesh tally approach. Difference between first and last layer is one magnitude of order. More exact results are expected with use change of fuel composition corresponding to burn-up in real core loading. The total neutron flux in irradiation channel for surveillance specimen is one order of magnitude higher that in RPV and as we can see from figure 10 and 12, the normalized spectrum of neutrons is different.

In future, we plan to improve mesh calculations and statistical parameters. Also, we will try to estimate DPA parameter.

Acknowledgement

Financial contributions from the grant VEGA 07/0129/09 is acknowledged.

References

  1. Odette, G., R., Lucas, G., E. (2001). In: Embrittlement of Nuclear Reactor Pressure Vessels: JOM journal, 7, 18-22
  2. X-5 Monte Carlo Team (2003). MCNP — A General Monte Carlo N-Particle Transport Code, Version 5 Los Alamos National Laboratory, Los Alamos
Co-authors of this paper are G. Farkas, V. Slugeň, S. Sojak, Slovak University of Technology, Faculty of Electrical Engineering and Information Technology, Ilkovičova 3, 812 19 Bratislava

Napísať príspevok