Individualizácia simulátora subjektu s diabetom 1. typu, časť 1.
27. Apríl, 2015, Autor článku: Tárník Marián, Informačné technológie, Medicína
Ročník 8, číslo 4  Pridať príspevok
Pridať príspevok
![]() Cieľom tejto práce je upraviť (individualizovať) parametre vybraných matematických modelov subjektu s diabetom 1. typu tak, aby ich výstupy zodpovedali dátam zo systému kontinuálneho monitorovania glykémie (CGM) od konkrétneho subjektu. Pre identifikáciu zodpovedajúcich podsystémov modelu sa tiež využijú dáta o farmakokinetike (PK, z angl. pharmacokinetics) a farmakodynamike (PD, z angl. pharmacodynamics) publikované v literatúre (viď. [7, 6]) konkrétneho inzulínu, ktorý používa subjekt.
Cieľom tejto práce je upraviť (individualizovať) parametre vybraných matematických modelov subjektu s diabetom 1. typu tak, aby ich výstupy zodpovedali dátam zo systému kontinuálneho monitorovania glykémie (CGM) od konkrétneho subjektu. Pre identifikáciu zodpovedajúcich podsystémov modelu sa tiež využijú dáta o farmakokinetike (PK, z angl. pharmacokinetics) a farmakodynamike (PD, z angl. pharmacodynamics) publikované v literatúre (viď. [7, 6]) konkrétneho inzulínu, ktorý používa subjekt.
1. Subjekt a CGM dáta
Sada dát použitá v tejto časti bola zozbieraná v rámci projektu DiaDAQ (Diabetic Data Acquisition), ktorý bol zameraný na získavanie dát v rozsahu kvalitného diabetického denníka (všeobecné diabetické dáta) doplneného o dáta zo systému pre kontinuálne monitorovanie glykémie. Ide o dáta od jedného subjektu, vek 14 rokov, hmotnosť [kg]. Subjekt používa inzulínovú pumpu s rýchlo účinkujúcim inzulínom NovoRapid (insulin Aspart). Informácie o farmakokinetike (PK) a farmakodynamike (PD) inzulínu Aspart sú publikované v literatúre [7, 6].
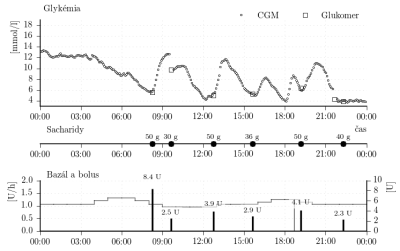
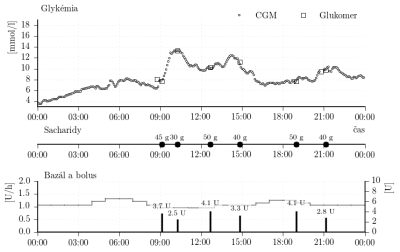
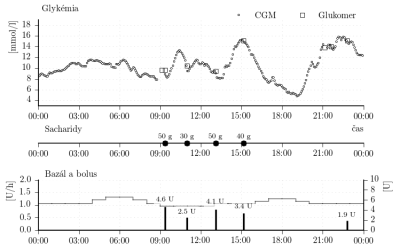
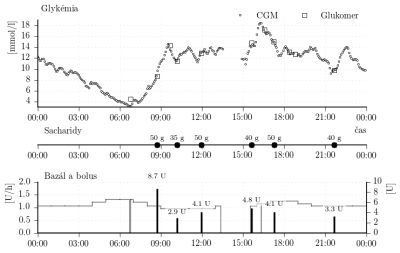
Ďalšie parametre súvisiace s konkrétnym uvažovaným subjektom sú nasledovné. Priemerná rýchlosť podávania bazálneho inzulínu počas 24 hodín je 1,09 [U/h]. Na základe meraní počas nocí uvažujeme, že táto rýchlosť podávania bazálneho inzulínu zodpovedá bazálnej glykémii [mmol/l]. Sada dát je rozdelená na štyri časti. Každá časť obsahuje dáta z jedného dňa. Celkovo sú teda k dispozícii dáta zo štyroch dní D00, D01, D02 and D03. Dáta sú zobrazené na nasledujúcich obrázkoch.
2. Simulátor s modelom podľa Bergmana
V tejto časti opíšeme matematický model, ktorý zahŕňa Bergmanov minimálny model inzulín-glukózovej interakcie [1]. V tomto prípade je model použitý ako základ simulátora subjektu s diabetom 1. typu.
2.1 Opis modelu
2.1.1 Bergmanov minimálny model
Bergmanov minimálny model pozostáva z dvoch diferenciálnych rovníc v tvare:
| (1) |
| (2) |
kde [mg/dl] je koncentrácia glukózy v krvi (glykémia),
[1/min] je obrátená hodnota časovej konštanty, ktorá udáva rýchlosť zmeny koncentrácie glukózy spôsobenej odchýlkou od bazálnej hodnoty glykémie
[mg/dl], parameter
[ml/
U/min] je známy ako index inzulínovej citlivosti a
[1/min je obrátená hodnota časovej konštanty. Hodnoty
[
U/ml] a
[mg/dl] sú bazálna koncentrácia inzulínu a bazálna koncentrácia glukózy v plazme (krvi) v uvedenom poradí. Parameter
[dl/kg] reprezentuje objem na kilogram telesnej hmotnosti
[kg], do ktorého sa distribuuje glukóza. Signál
[1/min] reprezentuje takzvaný inzulín vo vzdialenom kompartmente. V bazálnom (ustálenom) stave máme
a
. Vstupmi modelu sú koncentrácia inzulínu v plazme
[
U/ml] a rýchlosť prísunu glukózy do krvi (plazmy)
[mg/kg/min]. Vo všeobecnosti sú možné dva zdroje glukózového toku
. V prvom rade je to vstrebávanie glukózy z tráviaceho traktu do krvi. Potom je tiež možná priama intravenózna infúzia glukózy.
2.1.2 Podsystém vstrebávania inzulínu
Ďalším podsystémom prezentovaného modelu je podsystém vstrebávania inzulínu z podkožia do krvi [2, 3]. Výstupom podsystému je koncentrácia inzulínu v krvi . Rovnice podsystému sú nasledovné
| (3) |
| (4) |
| (5) |
kde [
U/kg/min] je rýchlosť podávania inzulínu do podkožia,
a
[
U/kg] reprezentujú množstvo inzulínu v jednotlivých kompartmentoch podsystému. Parameter
[min] je časová konštanta podsystému,
[1/min] je rýchlosť samovoľného ubúdania inzulínu v plazme a parameter
[ml/kg] reprezentuje objem na kilogram hmotnosti, do ktorého sa inzulín distribuuje.
2.1.3 Podsystém vstrebávania glukózy
Tretí podsystém opisuje vstrebávanie glukózy z tráviaceho traktu do krvi, teda výstupom podsystému je signál [mg/kg/min]. Rovnice podsystému sú v tvare
| (6) |
| (7) |
kde [mg/kg/min] je rýchlosť prijímania sacharidov v čase, presnejšie v okamihu začiatku, jedla, teda
je impulzom so šírkou zodpovedajúcou perióde vzorkovania a s plochou zodpovedajúcou množstvu prijatých sacharidov. Parameter
[min] je časová konštanta a
[bezrozmerné] je zlomok z prijatých sacharidov, ktoré sa efektívne vstrebú.
2.2. Prispôsobenie parametrov modelu
2.2.1 Podsystém vstrebávania inzulínu – PK dáta
Prvým krokom pri prispôsobovaní modelu je identifikácia parametrov podsystému vstrebávania inzulínu. Identifikácia je založená na využití dostupných dát o farmakokinetike (PK) daného inzulínu. Farmakokinetika inzulínu (Aspart) je znázornená na obr. 5. Bazálna koncentrácia inzulínu nameraných PK dát je 6,5 [U/ml]. Dáta boli získané technikou euglykemický clamp pričom bol podaný bolus 0,2 [U/kg] podkožne do abdominálnej steny, viď \cite{Mudaliar1999}. V tomto prípade bolus zodpovedá 12,88 [U], teda
[
U/kg/min] počas prvej periódy vzorkovania
, keď
[min] a v inom čase
. Priemerná rýchlosť podávania bazálneho inzulínu je známa zo záznamov inzulínovej pumpy subjektu. Priemer je 1,09 [U/h] čo zodpovedá
[
U/kg/min], kde index
označuje bazálnu rýchlosť. Výsledný signál
je súčtom bolusovej časti
a bazálnej časti
ako je znázornené na obr. 5.
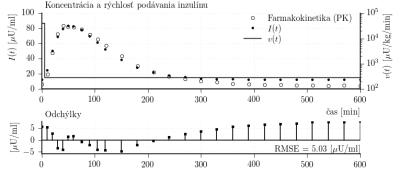
Obr. 5: Výsledok identifikácie podsystému vstrebávania inzulínu. Identifikované parametre sú [min],
[1/min] a
[dl/kg]. Uvažovaný bolus inzulínu 0,2 [U/kg] zodpovedá 12,92 [U].
V bazálnom (ustálenom) stave podsystému (3), pre dané , je bazálna koncentrácia inzulínu
daná množinou parametrov
,
a
. Avšak, impulzná charakteristika je, samozrejme, tiež daná touto množinou parametrov. Preto cieľom je identifikovať vektor neznámych parametrov
tak aby sa minimalizovala odchýlka medzi simulovanou koncentráciou inzulínu
a známym priebehom koncentrácie inzulínu, teda farmakokinetikou PK. Uvažujeme optimalizačný problém nelineárnej metódy najmenších štvorcov v tvare
| (8) |
kde je vektor nameraných hodnôt PK a
je vektor zodpovedajúcich simulovaných hodnôt. Uvažuje sa regularizácia, kde
je normálna (vyvodené z literatúry [3, 5]) hodnota distribučného objemu inzulínu. V tomto prípade
[dl/kg] a
je váhovací koeficient. Výsledné parametre podsystému sú
[min],
[1/min] a
[dl/kg]. Výsledný simulovaný priebeh koncentrácie inzulínu je porovnaný s nameraným priebehom na obr. 5.
2.2.2 Index inzulínovej citlivosti a doba účinku inzulínu (PD dáta)
V tomto kroku sa identifikujú parametre súvisiace s indexom inzulínovej citlivosti a z takzvanou dobou účinkovania inzulínu (angl. insulin action time), alebo dobou, počas ktorej je daný bolus aktívny. Konkrétne parametre a
. Tieto parametre určujú dynamiku signálu
. Princípom merania farmakodynamiky je udržiavanie ustálenej (bazálnej) koncentrácie glukózy (euglykemický clamp) v krvi po podaní bolusu inzulínu. Glykémia sa udržiava externou intravenóznou infúziou glukózy. Priebeh tejto infúzie zodpovedá farmakodynamike (PD dáta) a z princípu tiež signálu
v rovnici . PD dáta a zodpovedajúci signál
sú znázornené na obr. 6.
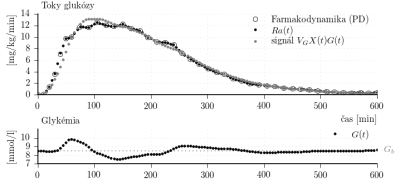
Obr. 6: Výsledok identifikácie indexu inzulínovej citlivosti a doby (dynamiky) účinku inzulínu. Identifikované parametre: [ml/
U/min] a
[1/min]. Signál
zodpovedá farmakodynamike (PD dátam).
Rovnica môže byť písaná v tvare
| (9) |
Počas euglykemického clamp-u, teda teoreticky , je možné predpokladať, že
. Potom parameter
má len minimálny vplyv pri dosahovaní
. Preto v simuláciách, kde
je dané PD dátami sa v tejto práci uvažuje
. Distribučný objem glukózy
je parameter, ktorý je vo vzťahu k telesnej hmotnosti. Je možné ho odhadnúť na základe hodnôt uvedených v literatúre, viď [3] a referencie tam uvedené. V tomto prípade sa uvažuje konštantná hodnota
[dl/kg], teda
[l/kg]. Cieľom je identifikovať vektor neznámych parametrov
tak aby bola odchýlka medzi simulovanou glykémiou a bazálnou hodnotou
(parameter subjektu) minimalizovaná. Hodnota
je predpokladaná ako daná a signál
je daný PD dátami. Úlohu je možné formulovať ako úlohu nelineárnej metódy najmenších štvorcov v tvare
| (10) |
kde je vektor simulovaných vzoriek glykémie. Pre identifikáciu s využitím PD dát sa použila hodnota
[mmol/l] (
[mg/dl]). Bolus inzulínu je rovnaký ako v predchádzajúcej časti (identifikácia s využitím PK dát). Výsledné identifikované parametre rovnice (1) sú
[ml/
U/min] a
[1/min]. Obr. ukazuje, že simulovaný priebeh glykémie
je udržiavaný dostatočne blízko bazálnej hodnoty. Z pohľadu simulačného modelu je to signálom
, ktorý zodpovedá účinku inzulínu v modely, teda úbytku glukózy. Keďže tento signál sa prakticky zhoduje so signálom
(prísun glukózy), glykémia ostáva nezmenená, teda na bazálnej úrovni.
2.2.3 Finalizácia individualizácie (CGM dáta)
Zvyšnými parametrami simulátora subjektu s diabetom 1. typu, ktoré je ešte potrebné identifikovať sú a
. Parameter
[bezrozmerné] je zlomok sacharidov, ktoré sa efektívne vstrebali (z celkového množstva podaných sacharidov). Hodnota tohto parametra je zvyčajne medzi
and
, [2, 3]. V tomto prípade uvažujeme
. Identifikácia je založená na CGM dátach. Na hornom panely obrázku 7 sú zobrazené reprezentatívne CGM dáta. Pre porovnanie sú zobrazené aj údaje z glukomera.
CGM dáta sú, samozrejme, závislé od dávkovania inzulínu a to aj bazálneho aj bolusového. Údaje o dávkovaní inzulínu sú zaznamenané v inzulínovej pumpe. Čas a množstvo prijatých sacharidov boli tiež zaznamenané v pumpe vzhľadom na použivanie bolus kalkulátora. Všetky spomenuté dáta boli použité ako vstup simulátora. Výstup podsystému vstrebávania inzulínu, ktorý bol identifikovaný v predchádzajúcich častiach, je znázornený na spodnom panely obrázka 7. Zvyšné skôr identifikované parametre boli tiež použité v simulátore. Cieľom je identifikovať vektor neznámych parametrov tak aby odchýlka medzi CGM dátami a výstupom simulátora bola minimalizovaná. V tomto prípade, dáta z intervalu 500 až 1200 minút z CGM dát uvedených na obr. 7 boli použité pre identifikáciu. Problém môže byť formulovaný ako úloha nelineárnej metódy najmenších štvorcov v tvare
| (11) |
kde je vektor nameraných CGM dát a
je vektor simulovaných hodnôt glykémie. Prvým výsledným je parameter
[min] z podsystému vstrebávania glukózy a druhým výsledným je parameter
[1/min]. Týmto je individualizácia simulátora založeného na Bergmanovom modely kompletná.
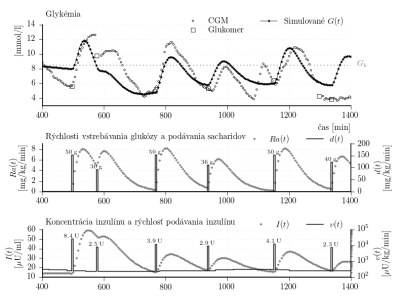
Obr. 7: Porovnanie CGM dát z výstupom individualizovaného simulátora subjektu s diabetom 1. typu. Identifikované parametre sú [1/min],
[min].
2.3. Validácia
V tejto časti je individualizovaný simulátor validovaný s využitím CGM dát z iných dní ako z dňa, z ktorého dáta boli použité pre identifikáciu. V simulátore sú použité parametre modelu identifikované v predchádzajúcich častiach. Hlavným účelom simulátora je simulácia priebehu glykémie. Vyhodnotenie a validácia je preto založená na porovnávaní simulovanej glykémie a nameraných CGM dát. Vyhodnocuje sa pomocou nasledujúcich metrík. VAF, z anglického percentage variance accounted for, ktorého hodnota je definovaná ako
| (12) |
kde je vektor nameraných CGM dát a
je vektor zodpovedajúcich výstupov modelu. VAF dvoch data vektorov, ktoré sú identické je 100 %. Ak sa odlišujú, hodnota je nižšia. Ďalej sa vyhodnocuje odmocnina so sumy štvorcov odchýlok (RMSE z angl. root mean square error) v tvare
| (13) |
kde je počet vzoriek v data vektore. Nakoniec sa vyhodnocuje jednoduché kritériu zhody SFM (z angl. simple fit metric) v tvare
| (14) |
kde je priemer prvkov dátového vektora
. SFM je rovnaká metrika ako fit [%] použitá v System Identification Toolbox pre {Matlab}, viď príručku používateľa alebo [4]. Model bol identifikovaný s využitím CGM dát z dňa D00. Avšak, ako bolo uvedené, nie všetky dáta v rámci dňa boli použité pre identifikáciu, len istý úsek. Tento úsek je vyznačený aj na vrchnom panely obrázku 8.
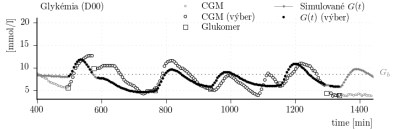
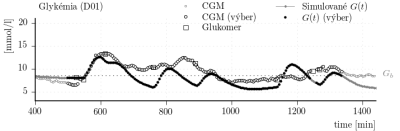
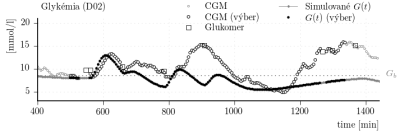
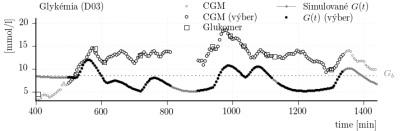
Obr. 8: Porovnanie CGM dát z každej sady so zodpovedajúcim výstupom individualizovaného simulátora.
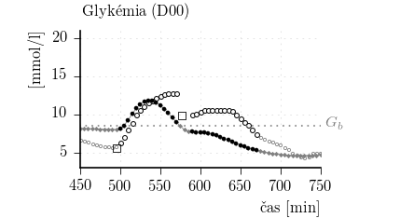
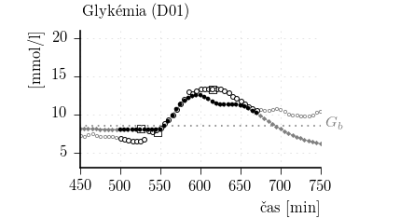
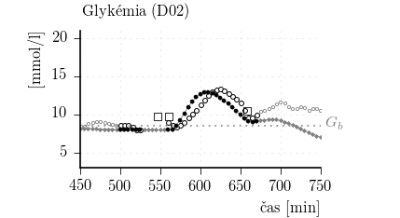
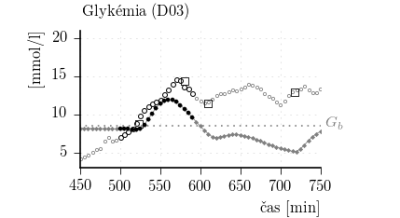
Obr. 9: Porovnanie CGM dát z obdobia raňajok z každého dňa zo simulovaným priebehom glykémie. Legenda ku grafom je zhodná z obr. 8.
Rovnaký úsek je použitý pre vyhodnotenie verifikácie modelu. Výsledky verifikácie sú sumarizované v tabuľke 1. Zvyšné dostupné dáta (z ostatných dní) boli použité pre validáciu modelu. Podobne ako pri verifikácii len zvolený úsek dát je porovnávaný pri vyhodnocovaní. Pre porovnanie vybrané CGM dáta a vybrané simulované dáta sú vyznačené na obr. 8. Výsledky validácie sú sumarizované v tabuľke 1.
Tab.1: Vyhodnotenie verifikácie simulátora subjektu s diabetom 1. typu.
| Data set | VAF [%] | RMSE [mmol/l] | SFM (fit) [%] |
| D01 | 54.37 | 1.64 | 30.78 |
Tab.2: Vyhodnotenie validácie simulátora subjektu s diabetom 1. typu.
| Data set | VAF [%] | RMSE [mmol/l] | SFM (fit) [%] |
| D02 | 9.22 | 2.14 | -17.31 |
| D03 | 13.92 | 3.62 | -27.82 |
| D04 | -25.53 | 5.82 | -195.56 |
Tab.3: Validácia modelu pre obdobie raňajok. Namerané CGM dáta a simulovaná glykémia sú na obr. 9.
| Data set | VAF [%] | RMSE [mmol/l] | SFM (fit) [%] |
| D01 | -26.61 | 2.5 | -51.63 |
| D02 | 84.93 | 1.00 | 60.61 |
| D03 | 70.71 | 0.98 | 45.35 |
| D04 | 71.26 | 1.8 | 25.30 |
Je možné povedať, že model v tvare a s vlastnosťami tak ako je tu prezentovaný nie je validný pre simuláciu celého dňa. Napriek úspešnej verifikácii modelu, teda, že model je schopný adekvátne simulovať dáta z dňa D00, model nie je vhodný pre simuláciu priebehu glykémie, ktorá je výsledkom každodenných podmienok života subjektu s diabetom 1. typu. Dôvodov je mnoho a súvisia s variabilitou fyziologických a klinických parametrov subjektu počas dňa. Navyše, vstupmi modelu sú len príjem sacharidov a dávkovanie inzulínu. Avšak faktorov ovplyvňujúcich glykémiu je veľké množstvo, napríklad fyzická aktivita, fyzický a psychický stav, choroby (chrípka a pod.), stres, atď.
Akokoľvek, je možné sa zamerať na malú časť dňa a vyhodnotiť úspešnosť simulácie pre tuto konkrétnu časť dňa. Konkrétne, vyhodnotenie obdobia raňajok je v tomto prípade užitočné. Výsledky validácie modelu pre obdobie raňajok sú sumarizované v tabuľke 3 a grafické porovnanie je na obr. 9. Pre obdobie raňajok je simulátor validný vzhľadom na to, že ak sa pri validácii uvažujú dáta len pre toto obdobie model dosiahne výrazne lepšie výsledky v porovnaní s výsledkami pre celý deň. Je možné usúdiť, že výhodnejšie je identifikovať parametre modelu separátne pre každé vhodné obdobie dňa (raňajky, obed, večera, noc a podobne). To je však už nad rámec práce prezentovanej v tomto článku.
Poďakovanie
Článok je jedným z výstupov výskumnej práce projektu s názvom “Centrum výskumu závažných ochorení a ich komplikácií”, “ITMS projektu: 26240120038″. “Projekt je spolufinancovaný zo zdrojov EÚ. Podporujeme výskumné aktivity na Slovensku”.
Literatúra
- R.N. Bergman, Y.Z. Ider, C.R. Bowden, and C. Cobelli. Quantitative estimation of insulin sensitivity. Am. J. Physiol. Endocrinol. Metab, 236(6):E667–E677, 1979.
- P. Herrero, P. Georgiou, N. Oliver, M. Reddy, D. Johnston, and Ch. Toumazou. A composite model of glucagon-glucose dynamics for in silico testing of bihormonal glucose controllers. Journal of Diabetes Science and Technology, 7(4):941–951, July 2013.
- Roman Hovorka, Valentina Canonico, Ludovic J Chassin, Ulrich Haueter, Massimo Massi-Benedetti, Marco Orsini Federici, Thomas R Pieber, Helga C Schaller, Lukas Schaupp, Thomas Vering, and Malgorzata E Wilinska. Nonlinear model predictive control of glucose concentration in subjects with type 1 diabetes. Physiological Measurement, 25(4):905, 2004.
- Lennart Ljung. System Identification (2nd Ed.): Theory for the User. Prentice Hall PTR, Upper Saddle River, NJ, USA, 1999.
- C.D. Man, R.A. Rizza, and C. Cobelli. Mixed meal simulation model of glucoseinsulin system. In Engineering in Medicine and Biology Society, 2006. EMBS ’06. 28th Annual International Conference of the IEEE, pages 307–310, 30 2006-sept. 3 2006.
- S.R. Mudaliar, F. A. Lindberg, M. Joyce, P. Beerdsen, P. Strange, A. Lin, and R. R. Henry. Insulin aspart (b28 asp-insulin): A fast-acting analog of human insulin. Diabetes Care, 22(9):1501–1506, September 1999.
- Novo-Nordisk. NovoRapid (insulin aspart) – Product Monograph. Watermeadow Medical, Two Rivers House, Station Lane, Witney, Oxfordshire OX28 4BH, UK on behalf of Novo Nordisk A/S, 2002.
Spoluautorom článku je Tomáš Ludwig, Ústav robotiky a kybernetiky, Fakulta elektrotechniky a informatiky, Slovenská technická univerzita v Bratislave