Spojitá waveletová transformácia a jej aplikácie
13. Júl, 2015, Autor článku: Zavacký Jozef, Elektrotechnika
Ročník 8, číslo 7  Pridať príspevok
Pridať príspevok
![]() Fourierova transformácia a jej nástroje sú úspešne aplikované v mnohých vedeckých oblastiach. Avšak, pomocou Fourierovej transformácie nie je možné analyzovať nestacionárne a prerušované signály súčasne v časovo-frekvenčnej rovine. Waveletová transformácia, ktorá bola v poslednej dobe objavená sa vysporiadala s obmedzeniami Fourierovej transformácie. Je to integrálna transformácia s jadrom, ktoré je odvodené z materského waveletu posunutím v čase a časovou kompresiou a dilatáciou. V tomto článku sú prezentované základy spojitej waveletovej transformácie spolu s jej hlavnými vlastnosťami a algoritmus výpočtu tejto transformácie. Následne sú uvedené typické príklady tejto transformácie pre vybrané signály.
Fourierova transformácia a jej nástroje sú úspešne aplikované v mnohých vedeckých oblastiach. Avšak, pomocou Fourierovej transformácie nie je možné analyzovať nestacionárne a prerušované signály súčasne v časovo-frekvenčnej rovine. Waveletová transformácia, ktorá bola v poslednej dobe objavená sa vysporiadala s obmedzeniami Fourierovej transformácie. Je to integrálna transformácia s jadrom, ktoré je odvodené z materského waveletu posunutím v čase a časovou kompresiou a dilatáciou. V tomto článku sú prezentované základy spojitej waveletovej transformácie spolu s jej hlavnými vlastnosťami a algoritmus výpočtu tejto transformácie. Následne sú uvedené typické príklady tejto transformácie pre vybrané signály.
1. Úvod
Na konci minulého storočia vznikol a v súčasnosti sa úspešne rozvíja nový a dôležitý smer v teórii a technike spracovania signálov, obrazov, a časových radov, ktorý sa nazýva waveletová transformácia (WT). Prvý “wavelet“ navrhol matematik A. Haar už v roku 1910 pri konštrukcii alternatívneho ortonormálneho systému k Fourierovmu [1]. Waveletova transformácia bola zavedená v polovici osemdesiatych rokov minulého storočia Morletom, Grossmanom a Mayerom, kedy bola použitá pri analýze vlastností seizmických a akustických signálov [2]. Exaktný matematický rámec bol postavený na myšlienke základného waveletu (wavelet- ”malá vlnka”, ”ondelette”) Francúzskou školou [2], [3] a je zdokumentovaný v Mayerovej knihe s názvom “Ondeletts” [4].
Ich práca poslúžila ako začiatok intenzívneho výskumu waveletov v nasledujúcom desaťročí radom vedcov takých, ako Dobechiesová, I., Mallat, S.G., Vetterli, M., Sweldens, W. Farge, G., Chui, C.K. a ďaľším. Waveletová trasnformácia je obzvlášť zaujímavá pre analýzu nestacionárnych signálov, pretože je alternatívou krátkodobej Fourierovej transformácie (Short-Time Fourier Transform) resp. Gaborovej transformácie [5-6]. Je tiež vo vzťahu s časovo-frekvenčnou analýzou založenou na Wigner-Willieho distribúcii [7-8]. WT signálov je zovšeobecnením spektrálnej analýzy vo vzťahu k Fourierovej aj krátkodobej Fourierovej transformácii. Využíva základné waveletové funkcie (wavelety resp. materské wavelety), ktoré môžu byť dilatované (alebo stláčané) a posúvané na základe dvoch parametrov: mierky a posunutia (časový posun). Ľubovoľný z najčastejšie používaných typov waveletov poskytuje úplný ortogonálny systém (bázu) funkcií.
V prípade waveletovej analýzy (dekompozície) signálu v spojení so zmenou veľkosti a šírky waveletu sú tieto schopné odhaliť rozdielnosť vlastností signálu pri rôznych škálach a prostredníctvom posunu je možné preanalyzovať vlastnosti signálu v rôznych bodoch na celom skúmanom intervale. Hlavne vďaka vlastnosti úplnosti tohto systému, je možné uskutočniť obnovenie (rekonštrukciu alebo syntézu) signálu prostredníctvom spätnej WT. Potvrdením dôležitosti WT je aj ten fakt, že algoritmy WT sú prezentované v široko používaných systémoch počítačovej matematiky, takých ako sú Mathcad, Matlab a Mathematica. WT môže byť predovšetkým rozdelená na spojitú waveletovú transformáciu (SWT) a diskrétnu waveletovú transformáciu (DWT), ktoré sú navzájom úplne rozdielne. SWT nachádza svoje použitie napr. v astronómii a astrofyzike [9-10], geofyzike [11-12], medicíne a biológii [13-14], hydrológii [15], geológii [16], financiách [17] atď.
2. Základy spojitej waveletovej transformácie a jej vlastnosti
Wavelety [18-19] sú časové funkcie vhodné pre analýzu značne premenlivých spojitých signálov. Tvoria jadro waveletovej transformácie a umožňujú zobrazenie signálov z časovej oblasti do časovo-mierkovej oblasti. Ich hlavnou výhodou je, že umožňujú získať v rôznych časoch a pri rôznych frekvenciách odlišné rozlíšenie. Spojitá waveletová transformácia signálu f(t) je definovaná nasledovne
| (1) |
kde symbol < > predstavuje skalárny súčin a je tzv. prototypová alebo základná waveletová funkcia, ktorá môže byť považovaná za impulznú charakteristiku pásmového filtra. Táto waveletová funkcia sa nazýva tiež základný (materský) wavelet (small wave – vlnka) a musí vyhovovať dvom podmienkam. Základné wavelety majú zvyčajne jednotkovú energiu, t. j.
. Faktor
v rov. (1) zabezpečuje zachovanie energie aj pri zmenenej mierke, t. j.
. Ďalšie waveletové funkcie (wavelety)
| (2) |
sa získajú z jediného základného waveletu pomocou šírkovej aj výškovej dilatácie a operácie časového posunu. Parameter posunutia “b“ určuje veľkosť posunutia waveletu na časovej osi a parameter šírkovej aj výškovej dilatácie (mierky) “a“ umožňuje meniť vzťah medzi časovým a frekvenčným rozlíšením. Ak bude a>1 wavelet sa roztiahne v časovej oblasti, čomu zodpovedá stlačenie vo frekvenčnej oblasti. Tým sa znižuje schopnosť rozlišovať signály v čase, ale získame väčšie frekvenčné rozlíšenie. Pre a&?lt;1 sa naopak wavelet stlačí v časovej oblasti, čomu zodpovedá roztiahnutie vo frekvenčnej oblasti. Týmto sa zvyšuje schopnosť rozlišovať signály v čase a znižuje sa schopnosť frekvenčného rozlíšenia.
SWT je ako to vyplýva z jej názvu spojitá transformácia. Počítač však pracuje so vzorkami signálu a teda i s diskrétnymi posunmi v čase b a parametra mierky a. Výsledkom je konečný počet waveletových koeficientov SWT{f(t),a,b}, ktoré aproximujú spojitý priebeh v časovo-mierkovej oblasti. Pokiaľ signál obsahuje napr. nejakú diskontinuitu v čase t = t1, bude pre malú hodnotu parametra mierky a pri časovom posunutí b = t1 táto diskontinuita s komprimovaným waveletom korelovať a hodnota koeficientu SWT{f(t),a,b} pre dané hodnoty parametrov a a b bude relatívne vysoká. Diskontinuita bude presne lokalizovaná v čase b = t1. Pri použití Fourierovej transformácie by sme v spektre síce videli frekvenčné zložky na vyšších frekvenciách, ale nemali by sme žiadnu informáciu o tom, kde se diskontinuita nachádza. Algoritmus výpočtu SWT podľa definičného vzťahu (1) možno zhrnúť do šiestich bodov
- Na začiatku výpočtu sa nastaví hodnota parametra mierky a (typicky a = 1) a hodnota posunu v čase b = 0 s.
- Wavelet s parametrom mierky a a časovým posunom b sa najprv vynásobí s vyšetrovaným signálom.
- Integráciou súčinu cez všetky časy t sa získa waveletový koeficient SWT{f(t),a,b}, ktorý vyjadruje mieru podobnosti waveletu s daným úsekom signálu. Čím väčšia je hodnota koeficientu, tým väčšia je podobnosť medzi waveletom a príslušným úsekom signálu.
- Potom sa wavelet posunie o malú hodnotu vpravo, tj. zvýší se hodnota časového posunu b. Kroky 2. až 4. se opakujú tak dlho, dokedy nie je pre danú mierku a vyšetrený celý časový priebeh signálu.
- Teraz sa zmení hodnota parametra mierky a, hodnota času b se nastaví na t = 0 s a začne se od kroku 2.
- Kroky 2. až 5. sa opakujú pre všetky parametre mierky a zo zvoleného intervalu hodnôt.
Ako môžu vyzerať základné wavelety je znázornené na Obr. 1, kde db1, db2, db5 a db10 sú Daubechiesovej wavelety. Existuje množstvo základných waveletov a s nimi aj mnoho systémov waveletových funkcií ako aj waveletových transformácií, ktoré majú odlišné vlastnosti. Keď sú parametre a aj b spojité, waveletová transformácia je vysoko redundantná a zodpovedajúca spätná transformácia nie je jednoznačná. Spojitá waveletová transformácia má menší praktický význam ako jej diskrétna alternatíva a preto sa skôr používa na interpretáciu jej všeobecnej podstaty.
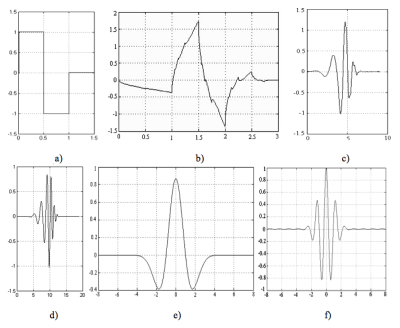
Obr. 1. Príklady waveletov a) Haarov wavelet (db1), b) db2, c) db5, d) db10, e) wavelet tvaru mexického klobúka, f) Morletov wavelet.
Ako je vidieť z rov.(1) hodnoty spektra SWT{f(t),a,b}, ktoré je dvojrozmernou funkciou, sú dané korelačným integrálom medzi spojitým signálom f(t) a funkciou ψa,b(t). Táto korelácia je mierou podobnosti medzi signálom a dilatovaným a posunutým waveletom. Čím bude parameter mierky a menší, tým bude wavelet v čase užší (komprimovanejší) a bude korelovať s vyššími frekvenciami obsiahnutými v signáli. Zväčšováním hodnoty parametra mierky a docielime rozšírenie (dilatáciu) waveletu v čase a wavelet bude korelovať s nízkými frekvenciami signálu. Pre konštantnú hodnotu mierky a je možné sa pozerať na SWT aj druhým spôsobom a to ako na konvolúciu signálu f(t) s časovo otočeným šírkovo a výškovo dilatovaným waveletom.
| (3) |
kde
| (4) |
čo je možné interpretovať ako prechod signálu f(t) cez filter, ktorého impulzná charakteristika je ga(t) ako to vidno na Obr.2. Výstup z filtra je totožný so SWT pre čas t a danú mierku a.
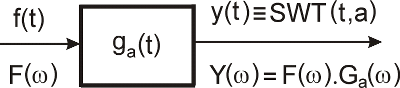
Obr. 2. Interpretácia SWT ako pásmového filtra.
Frekvenčná charakteristika tohto filtra je
| (5) |
kde je Fourierova transformácia waveletu
. SWT je invertovateľná, ak pre
základného waveletu platí tzv. podmienka prípustnosti [4],
| (6) |
Aby bola splnená podmienka (6) základný wavelet musí vyhovovať dvom podmienkam. Musí to byť oscilačná funkcia s nulovou strednou hodnotou
| (7) |
a musí konvergovať k nule pre . Druhá podmienka, ktorej musí základný wavelet vyhovovať je
| (8) |
Okrem toho musí rýchlo klesať pre
a pre
. To znamená, že
musí byť impulzná charakteristika pásmového filtra. Potom existuje inverzná SWT v tvare
| (9) |
Vlastnosti SWT
SWT má viecero užitočných vlastností, pričom základné z nich si uvedieme.
1) Linearita
| (10) |
Linearita priamo vyplýva z vlastností skalárneho súčinu v rov. (1).
2) Invariancia v čase
| (11) |
Invariancia v čase popisuje skutočnosť, že posun analyzovanej funkcie po časovej osi spôsobí rovnaký posun waveletových koeficientov po osi posunu. Túto skutočnosť je možné odvodiť z predstavy, že SWT môže byť interpretovaná pomocou množiny lineárnych časovo invariantných filtrov. Táto vlastnosť sa stráca pri prechode k diskrétnej waveletovej transformácii.
3) Zmena mierky
| (12) |
Vzťah popisuje závislosť medzi SWT originálnej funkcie a jej roztiahnutou alebo stlačenou podobou, vo waveletových koeficientoch dôjde k adekvátnemu roztiahnutiu alebo stlačeniu v osi mierky a v osi posunu .
4) Zachovanie energie – pre a jeho
platí
| (13) |
Energia signálu v časovej a časovo-mierkovej oblasti sa zachováva. Jedná sa o analógiu Parsevalovej teorémy v prípade ortgonálnej waveletovej bázy.
5) Detekcia singularít – označme Diracov impulz v čase t0 ako δ(t-t0). Jeho SWT je
| (14) |
6) Diferencovateľnosť
| (15) |
3. Časovo-mierková rovina SWT
Aby sme mohli opísať časovo-frekvenčné rozlíšenie spojitej waveletovej transformácie uvažujme časovo-frekvenčné okno zodpovedajúce príslušnému waveletu . Jeho stred je v bode Stω(t0,ω0) a veľkosti strán sú 2
a 2
. Príslušné parametre sa vypočítajú analogicky ako pre KDFT takto [20]
| (16) |
| (17) |
| (18) |
| (19) |
Pre stred Stω(t0,ω0) a veľkosti (smerodajné odchylky) a
výškovo a šírkovo dilatovaného waveletu
nastanú zmeny (dostávame)
, \{ a. \Delta_t, \Delta_{\omega } /a \}. To znamená, že waveletová transformácia SWT{f(t),a,b} poskytuje informáciu o signáli f(t) a jeho spektre F(ω) v časovo-frekvenčnom okne
| (20) |
Plocha okna je nezávislá od parametrov a a b, je určená iba použitým waveletom
. Okno (časová súradnica okna) sa zužuje, keď sa parameter a zmenšuje a opačne. Na druhej strane okno (frekvenčná súradnica okna) sa rozširuje, keď sa parameter a zmenšuje a opačne ako to vyplýva zo vzťahu (4) a (5). Obr. 3 nám ilustruje rozlíšenie waveletovej transformácie pre rozdielne parametre a1, a2 a b1, b2, pričom b2 > b1 a a2 > a1.
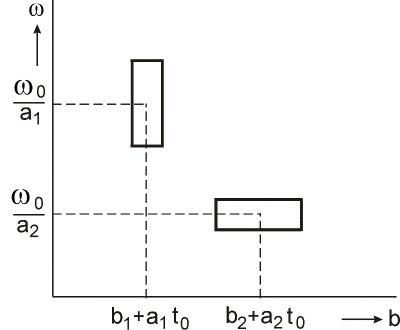
Obr. 3. Časovo-frekvenčné rozlíšenie spojitej waveletovej transformácie v časovo frekvenčnej rovine.
Z vyššie uvedeného vyplýva aj ďalšia dôležitá vlastnosť a to, že pomer výšky okna a polohy stredu okna vo frekvencii ostáva stále konštantný. Označme ho . Platí
. Analogicky s teóriou rezonančných obvodov sa označuje ako kvalita waveletu. Pretože funkcia analýzy
je šírkovo aj výškovo dilatovaná a nie modulovaná ako je tomu u jadra KDFT, waveletová analýza je často nazývaná časovo-mierkovou analýzou na rozdiel od časovo-frekvenčnej analýzy.
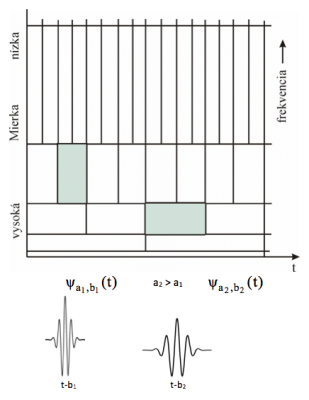
Obr. 4. Dve základné operácie s waveletom, zmena mierky a posun v čase definujú pokrytie časovo-mierkovej roviny oknami.
Waveletová transformácia obchádza Heisenbergov princíp neurčitosti tým, že poskytuje dobré časové rozlíšenie na vyšších frekvenciách a dobré frekvenčné rozlišením na nízkych frekvenciách, čo zodpovedá zlému rozlíšeniu v mierke na nízkých frekvenciách. Frekvenčná os je však nahradená parametrom zmeny mierky a, takže ide o zobrazenie v tzv. časovo-mierkovej rovine. Vzťah medzi mierkou a frekvenciou je taký, že malé hodnoty mierky odpovedajú vysokým frekvenciám a opačne vysokým hodnotám mierky odpovedajú nízke frekvencie. Zobrazenie na Obr.4 sa všeobecne používa pre vysvetlenie ako je možné interpretovať časové a frekvenčné rozlíšenie. Spektrum SWT sa vyjadruje vo forme škálogramu. Škálogram (angl. scalogram) sa nazýva graf, v ktorom je zobrazena hustota (množstvo) energie pre danú mierku a a pozíciu b waveletu (v Heisenbergovom okne waveletu ). Vypočíta sa ako kvadrát zo spektra SWT, t.j.
| (21) |
Rozdiel oproti spektrogramu u krátkodobej Fourierovej transformácie spočíva v obrátenej orientácii osi a, resp. f. Presnejšie povedané, frevencia je nepmiamo úmerná mierke.
| (22) |
Zo znalosti centrálnej frekvencie fc možno ľahko vypočítať vzťah medzi mierkou a frekvenciu
| (23) |
kde
| (24) |
Vzťah medzi mierkou a frekvenciu napr. pre wavelet ‘dB1′ je možné vypočítať pomocou Matlabu použitím príkazu scal2frq takto
Fs = 1000;
wname = 'dB1';
scales = 1:1:128;
TAB_Sca2Frq = scal2frq(scales,wname,1/Fs);
clf
plot(TAB_Sca2Frq,'r');
axis tight
grid
hold on
plot([scales(1),scales(end)]);
ylim([0 100]);
xlabel('mierka\it a\rm [-]');
ylabel('frekvencia\it f\rm [Hz]');
Závislosť medzi mierkou a a frekvenciou f pre wavelet dB1 je zobrazená na Obr.5
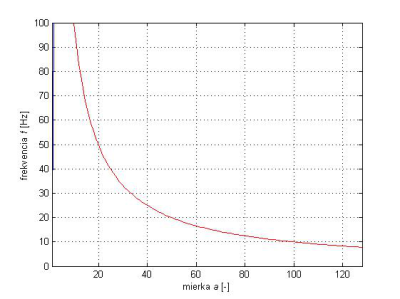
Obr. 5 Závislosť medzi mierkou a frekvenciou pre wavelet dB1.
3. Experimenty
Uvažujme prípad harmonického signálu s frekvenciou 4 [kHz] s dvomi diskontinuitami v čase 0.3 [s] a 0.7 [s] podľa Obr.6. Zodpovedajúci škálogram je na obr.7 a jeho trojrozmerná (3R) verzia na obr.8.
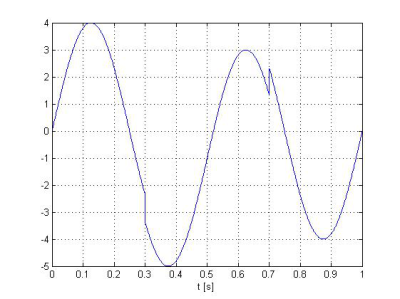
Obr. 6 Harmonický signál f(t) = 4sin(4πt) s dvomi diskontinuitami v čase 0.3 [s] a 0.7 [s].
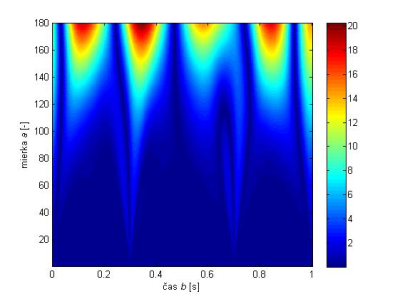
Obr. 7 Škálogram signálu f(t) z obr.6, použitý bol wavelet sym4.
Zo škálogramov na Obr.7 a Obr.8 vidieť presnú lokalizáciu diskontinuít v čase b = t1 = 0.3 [s] a v čase b = t2 = 0.7 [s]. Ďalej je zrejmé zhoršovanie časového rozlíšenia s rastúcou mierkou a (klesajúcou frekvenciou). Diskontinuity v časech = 0 [s] a = 1 [s] sú spôsobené obmezenou dĺžkou signálu.
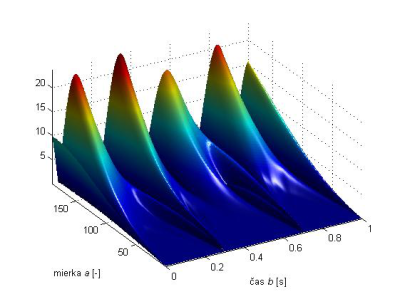
Obr. 8 3R škálogram signálu f(t) z obr.6, použitý bol wavelet sym4.
Uvažujme kosínusový signál s lineárne rozmietanou frekvenciou vygenerovaný v programe Matlab pomocou funkcie chirp s frekvenciou 0 [Hz] v čase t = 0 [s] a 75 [Hz] v čase t = 0.5 [s], ktorý je zobrazený na Obr.9.
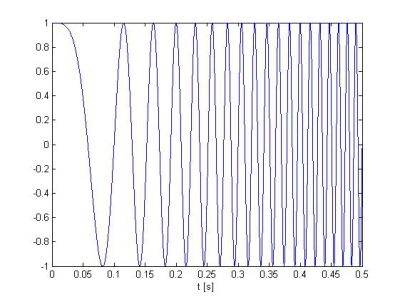
Obr. 9 Kosínusový signál s lineárne rozmietanou frekvenciou vygenerovaný v Matlabe pomocou funkcie chirp.
Škálogram tohto signálu je na Obr.10, pričom bol použitý wavelet sym4. Z obrázku je zrejmé, že vysoké frekvencie majú dobré rozlíšenie v mierke (t.j. zlé rozlíšenie vo frekvencii) a dobré rozlíšenie v čase (v grafe vpravo dole), zatiaľ čo nízke frekvencie majú dobré rozlíšenie vo frekvencii (zlé rozlíšenie v mierke) a zlé rozlíšenie v čase (v grafe vľavo).
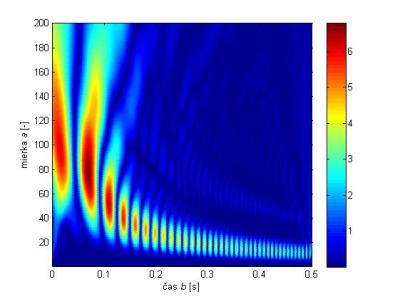
Obr. 10 2R škálogram signálu chirp s lineárne rastúcou frekvenciou pre wavelet sym4.
Ďalej vykonáme waveletovú analýzu dvoch rôznych elementárnych signálov. Prvým bude harmonický sínusový signál s frekvenciou 10 [Hz] na Obr.11.
Fs = 1000;
t = 0:1/Fs:1;
f1 = 10;
x = sin(2*pi*t*f1);
plot(x,'r'); axis tight
xlabel('čas [ms]')
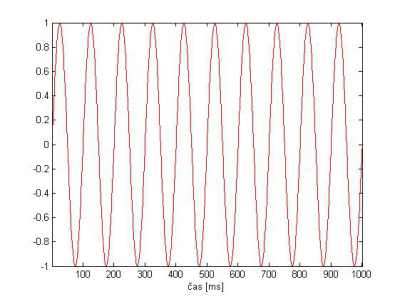
Obr. 11 Harmonický sínusový signál.
Teraz vypočítame SWT s použitím waveletu gaus4 a navrhneme postup ako nájsť frekvenčnú informáciu.
wname = 'gaus4';
scales = 1:1:128;
coefs = cwt(x,scales,wname);
Keď použijeme funkciu scal2freq môžeme vypočítať a graficky zobraziť závislosť medzi mierkou a a frekvenciou f (Obr.12). Táto závislosť ako bolo ukázané vyššie závisí na zvolenom wavelete. Hľadáme mierku, ktorá zodpovedá frekvencii f1 analyzovaného signálu.
TAB_Sca2f1 = scal2frq(scales,wname,1/Fs);
clf;
plot(TAB_Sca2f1); axis tight; grid
hold on
plot([scales(1),scales(end)],[f1 f1],'m--')
set(gca,'YLim',[0 100])
xlabel('mierka\it a \rm[-]');
ylabel('frekvencia\it a \rm[Hz]');
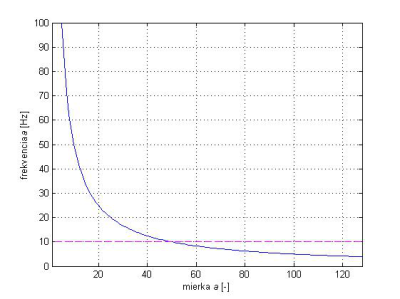
Obr. 12 Závislosť medzi mierkou a frekvenciou pre wavelet gaus4.
Hľadáme mierku Sca prislúchajúcu frekvencii f1 pre wavelet gaus4.
[~,idxSca] = min(abs(TAB_Sca2f1-f1));
Sca = scales(idxSca)
Hodnota tejto mierky je Sca = 50. Teraz použijeme SWT pre výpočet škálogramu waveletových koeficientov pre wavelet gaus4. Graficky zobrazíme tento škálogram a horizontálnu čiaru pre mierku Sca spojenú s frekvenciou f1. Na Obr.13 môžeme vidieť, že táto priamka spája maximálne hodnoty energie v škálograme.
wscalogram('image',coefs,'scales',scales,'ydata',x);
hold on
plot([1 size(coefs,2)],[Sca Sca],'Color','m','LineWidth',2);
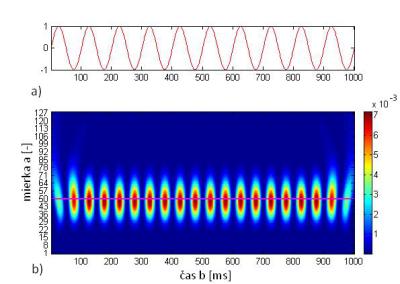
Obr. 13 a) Analyzovaný signál, b) škálogram.
Maximálne hodnoty energie v škálograme sú detekované pre mierku 50, čo prislúcha frekvencii 10 [Hz], ako to vidno z Obr.12. Toto je metóda ako použiť waveletovú analýzu pre nájdenie frekvenčnej informácie. Na Obr.14 je zobrazené iné, tzv. obrysové vykreslenia škálogramu pre určenie frekvenčnej informácie.
clf; coefs = cwt(x,scales,wname,'scalCNT');
hold on
plot([1 size(coefs,2)],[Sca Sca],'Color','m','LineWidth',2);
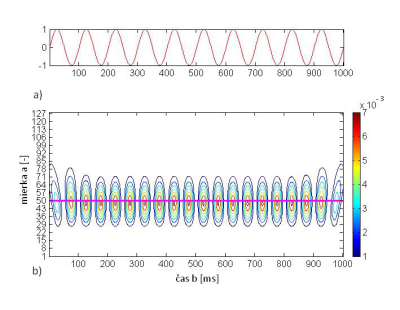
Obr. 14 a) Analyzovaný signál, b) škálogram.
Lokalizácia frekvenčnej informácie v škálograme závisí na wavelete použitom pre nanalýzu. Niektoré iné wavelety sú taktiež veľmi dobre vhodné pre tento cieľ. Druhým signálom pre waveletovú analýzu bude zložitejší periodický signál, ktorý je sumou dvoch periodických signálov s frekvenciami f1=10 [Hz] a f2=40 [Hz]. Vypočítame SWT s použitím waveletu gaus4 a navrhneme postup ako nájsť frekvenčnú informáciu. Analyzovaný signál s(t) = sin(2πf1t) + sin(2πt*f2t) je na Obr.15.
f1 = 10;
f2 = 40;
Fs = 1000;
t = 0:1/Fs:1;
s = sin(2*pi*t*f1) + sin(2*pi*t*f2);
clf; plot(s,'r'); axis tight
xlabel('čas [ms]')
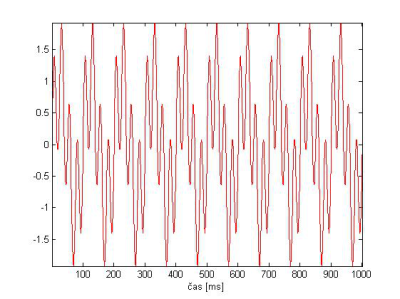
Obr .15 signál x(t) = sin(2πf1t) + sin(2πt*f2t).
Vypočítame SWT signálu s(t) a potom zobrazíme škálogram ako to vidno na Obr.16. Na tomto obrázku sú tiež zobrazené dve horizontálne čiary spájajúce lokálne maximá energie tohto škálogramu prislúchajúce mierkam Sca_1 and Sca_2, ktoré sú spojené s frekvenciami f1 a f2.
f1 = 10;
f2 = 40;
Fs = 1000;
t = 0:1/Fs:1;
s = sin(2*pi*t*f1) + sin(2*pi*t*f2);
clf;
wname = 'gaus4';
scales = 1:1:80;
coefs = cwt(s,scales,wname);
TAB_Sca2f1 = scal2frq(scales,wname,1/Fs);
clf;
figure(1);
plot(TAB_Sca2f1); axis tight; grid
hold on
plot([scales(1),scales(end)],[f1 f1],'m--')
set(gca,'YLim',[0 100])
hold on
plot([scales(1),scales(end)],[f2 f2],'g--')
set(gca,'YLim',[0 100])
xlabel('mierka\it a \rm[-]'); ylabel('frekvencia\it f \rm[Hz]');
[~,idxSca_1] = min(abs(TAB_Sca2f1-f1));
Sca_1 = scales(idxSca_1)
[~,idxSca_2] = min(abs(TAB_Sca2f1-f2));
Sca_2 = scales(idxSca_2)
figure(2);
wscalogram('image',coefs,'scales',scales,'ydata',s);
hold on
plot([1 size(coefs,2)],[Sca_1 Sca_1],'Color','m','LineWidth',2);
plot([1 size(coefs,2)],[Sca_2 Sca_2],'Color','m','LineWidth',1);
figure(3);
coefs = cwt(s,scales,wname,'scalCNT');
hold on
plot([1 size(coefs,2)],[Sca_1 Sca_1],'Color','m','LineWidth',2);
plot([1 size(coefs,2)],[Sca_2 Sca_2],'Color','m','LineWidth',1);
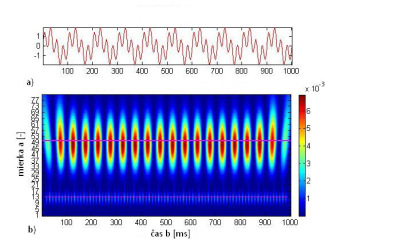
Obr. 16 a) Analyzovaný signál, b) škálogram.
Obr.17 zobrazuje alternatívne obrysové vykreslenia škálogramu z Obr.16 .
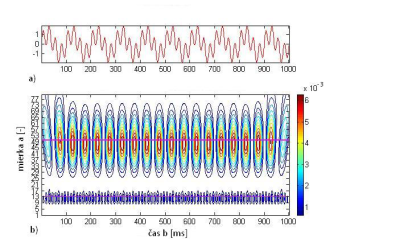
Obr. 17 a) Analyzovaný signál, b) škálogram.
Pre mierky Sca_1 = 50 a Sca_2 = 13 z Obr.18 určíme nakoniec frekvencie f1=10 [Hz] a f2=40 [Hz].
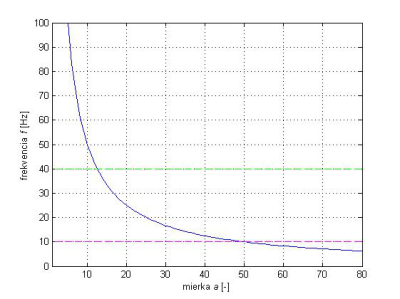
Obr. 18 Závislosť medzi mierkou a frekvenciou pre wavelet gaus4.
Pomocou SWT možno tiež dobre určiť harmonické signály (ich frekvencie) zo signálu daného súčtom harmonických signálov a bieleho šumu.
3. Záver
Po teoretickej analýze SWT boli vypočítané a zobrazené škálogramy pre harmonický signál s dvomi diskontinuitami v čase, pričom pomocou vypočítaného škálogramu boli určené časové okmžiky týchto diskontinuít . Zo škálogramu signálu s rozmietanou frekvenciou je zrejmé, že vysoké frekvencie majú dobré rozlíšenie v mierke, zatiaľ čo nízke frekvencie majú dobré rozlíšenie vo frekvencii. Pre harmonický signál a potom súčet dvoch harmonických signálov je pomocou ich škálogramov a nelineárnej závislosti medzi mierkou a frekvenciou možné určiť hodnoty frekvencií harmonických signálov.
Literatúra
- A. Haar, “ Zur Theorie der orthogonalen Funktionensysteme“, Mathematische Annalen, 69, 1910, p. 331–371.
- P. Goupillaud, A. Grossmann, J. Morlet, J, “Cycle-octave and related transorms in seismic signal analysis. Geoexploration“, Vol. 23, 1984, p. 85- 102.
- A. Grossmann, J. Morlet, “Decomposition of Hardy functions into square integrable wavelets of constant shape“, SIAM J. Anal. 15, p. 723-736, 1984.
- Y. Meyer, “Ondelettes, vol. 1 of Ondelettes et Opérateurs“, Paris: Hermann, 1990.
- S. Qian,D. Chen, “Joint Time-Frequency Analysis – Methods and Applications, (chap.3 Gabor Expansion – Inverse Sampled STFT) “, 2011, ISBN 0-13-254384-2.
- J. Zavacký, “Krátkodobá Fourierova transformácia“, Posterus, Roč. 7, č. 12, 2014, p. 1-11, ISSN 1338-0087
- L. Cohen, “Time Frequency Analysis: Theory and Applications“, Prentice Hall (Chapter 8), 1995, ISBN: 9780135945322.
- B. Boashash, “Note on the Use of the Wigner Distribution for Time Frequency Signal Analysis“, IEEE Transactions on Acoustics, Speech, and Signal Processing, Vol. 36, No. 9, 1988, p. 1518–1521.
- J. P. Antoine et al, , “Two Dimensional Wavelets and their Relatives “,Cambridge UK, New York,2004.
- E. Slezák, A. Bijaoui, G. Mars, “Idetification of Structures from Galaxy Counts. Use of the Wavelet Transform“, Astron. Astroph.,Vol. 227, 1990, p. 301-316.
- E. Foufoula-Georgiou, P. Kumar, “Wavelets in Geophysics“, 1994, Academic, San Diego, Calif., 384 p.
- M.E. Everet, “Near Surface Applied Geophysics“,Cambridge University Press, New York,2013.
- A. Albroubi, M. Unser, “Wavelets in Medicine and Biology“,CRC Press, 1996.
- M. N. Varma, A. Chatterjee, “In Molecular Radiation Biology, Monte Carlo Methods“,Plenum Press, New York. 1994.
- B.Sivakumar, R. Berndtsson, “Advances in Data-Based Approaches in Hydrogeologic Modeling and Forecasting “,World Scientific Publishing Co. Pte. Ltd., 2010.
- B.Hobss, A. Ord, “Structural Geology,The Mechanics of Deforming Metamorphic Rocks“, Elsevier Inc.,Nethelands,2015.
- F. In, S. Kim, “An Introduction to Wavelet theory in Finance, A Wavelet Multiscale Approach“,World Scientific Publishing Co. Pte. Ltd.,USA, 2013.
- S. Mallat, “A Wavelet Tour of Signal Processing“, Academic Press, 2009, ISBN 13: 978-0-12-374370-1.
- J. Zavacký, J.Mihalík, J, “Algoritmus vypočtu waveletov pomocou banky zrkadlových filtrov“, Acta Electrotechnica et informatica, Vol.5, No.1, 2005, s.42-49.
- A. Mertins, “Signal Analysis, Wavelets, Filter Banks, Time Frequency Transforms and Applications “, John Wiley and Sons, New Jersy, 1999.

