Príspevok sa venuje predstaveniu algoritmu Houghovej transformácie (HT). Po opísaní pôvodného návrhu sú zmienené aj rôzne verzie tejto transformácie, ktoré si našli svoje uplatnenie v oblasti rozpoznávania obrazcov. Samotná HT má viacero krokov, ktoré sú v článku bližšie popísané. Pozornosť je venovaná aj zostaveniu akumulátora, rozsahu a rozlíšeniu jeho parametrov. Po uvedení vlastností a možností transformácie je rozpoznávanie tvaru dopravnej značky demonštrované na jednoduchom príklade.

1. Úvod

Vývoj algoritmu, ktorý dnes poznáme ako Houghovu transformáciu (HT) začal koncom 50. rokov minulého storočia. V tejto dobe sa Paul V. C. Hough snažil o vytvorenie postupu, ktorý by bol schopný odhaliť dráhy častíc v hmlových komorách. Tieto zariadenia obsahujú kvapalinu, ktorá sa zahreje tesne pod bod varu. Po znížení tlaku v komore vytvárajú pohybujúce sa častice okolo svojich dráh malé bublinky. Svoje výsledky Hough zhrnul v práci [1].

Po nástupe počítačov, ktoré boli schopné pracovať s dostatočne veľkým množstvom dát sa začala rozvíjať oblasť spracovania obrazu. Do tejto oblasti patria aj postupy, ktoré vyhľadávajú určité tvary, alebo celé obrazce (angl. pattern recognition). Pre účely rozpoznávania parametrizovateľných tvarov bol vytvorený nástroj, ktorý bol autormi R. O. Dudom a P. E. Hartom nazvaný zovšeobecnenou Houghovou transformáciou (GHT, angl. generalized Hough Transform) [2, 3]. GHT bola spočiatku používaná na extrakciu priamok zo zvoleného obrazu (môžu byť definované dvojicou parametrov), neskôr sa objavili aj postupy pracujúce s trojicou parametrov, ktoré sú schopné nájsť kružnice. Používanie väčšieho množstva parametrov nie je vhodné z hľadiska lineárne rastúcej výpočtovej náročnosti [4].

Neskôr bola pozornosť venovaná možnosti spracovania ľubovoľných obrazcov, ktoré by sa dali rozdeliť na viacero jednoducho parametrizovateľných. Takýto postup je bližšie popísaný v [5]. Jeho autor, D. H. Ballard zostavil množinu tvarov, ktoré sa vyhľadávajú v zvolenom obraze. Patria tu priamky, kruhy (resp. kružnice), paraboly a elipsy, prípadne ich časti, resp. výseky. Pre dosiahnutie vyššej úspešnosti vyhľadávania sa pracuje s rôzne posunutýni, otočenými a škálovanými (zmena mierky) verziami týchto tvarov. Nevýhodou tohto algoritmu je rovnako ako v prípade HT s viacerými parametrami jeho výpočtová náročnosť.

2. Opis krokov algoritmu HT

Keďže HT prehľadáva body zvoleného obrazu a určuje ich prítomnosť v rôznych tvaroch (resp. v ich obrysoch), je vhodné počet takýchto bodov minimalizovať. Pre tieto účely je možné využiť detektory hrán. Ku najznámejším z nich patria Cannyho detektor [6], Prewittovej [7] a Sobelov operátor [8]. Hrany určené Cannyho detektorom ukazuje Obr. 1.

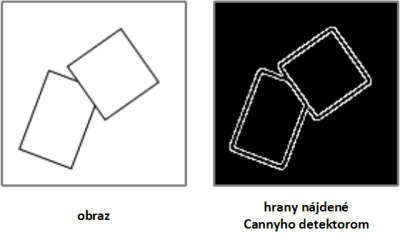
Obr. 1 Výsledok detekcie hrán Cannyho detektorom

Ďalším krokom algoritmu je vytvorenie všetkých možných tvarov. Tvary sú popísané ich parametrami. V prípade pôvodného Houghovho návrhu [1] boli použivané parametre smernicového vyjadrenia priamok (rovnica y = kx + q), čo však spôsobovalo problémy pri vyhľadávaní zvislých priamok. Tento problém bol vyriešený v [2], kde sa využívajú polárne súradnice. Súradnicami priamky sú polomer od stredu súradnicového systému ρ a uhol θ zovretý priamkou a x-ovou osou súradnicového systému. Rôzne druhy vyjadrenia pozície súradníc ukazuje Obr. 2.

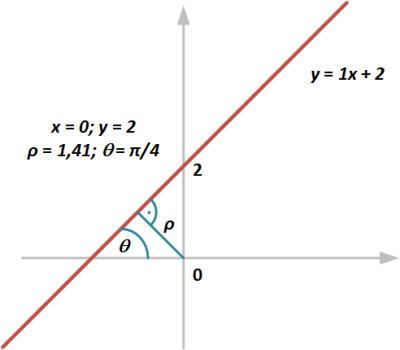
Obr. 2 Rozdiel medzi smernicovým a polárnym vyjadrením súradníc

Po vytvorení všetkých možných tvarov sa vyšetruje prítomnosť bodov získaných po detekcii hrán v týchto tvaroch, resp. ich obrysoch. Ak je bod obsiahnutý v tvare, tento tvar získa hlas (angl. vote). Hlasy sa ukladajú do tzv. akumulátora (niekedy nazývaný aj akumulačnou maticou). Celý proces sa nazýva ako hlasovacia procedúra (angl. voting procedure). Príklad akumulátora je zobrazený na
Obr. 3. Keďže v tomto prípade sa v obraze vyhľadávali priamky, akumulátor je dvojrozmernou maticou (na jednej osi je polomer ρ a na druhej uhol θ ). V prípade prehľadávania tvarov s viacerými parametrami by bolo nutné vytvoriť viacrozmerné akumulátory.

Obr. 3 Dvojrozmerný akumulátor vytvorený pri vyhľadávaní priamok

Pre lepšie zobrazenie je vhodné vykonať ekvalizáciu histogramu akumulátora, rovnako ako na Obr. 3. Ekvalizáciou histogramu sa získa väčší dynamický rozsah početnosti hlasov. Pri tvorbe akumulátora je potrebné zvážiť aj rozlíšenie a rozsah parametrov na jeho osiach. Jemnejšie rozlíšenie znamená väčší počet tvarov, pre ktoré bude vykonávaná hlasovacia procedúra. Rozsah parametrov taktiež ovplyvňuje prehľadávanú množinu tvarov, v niektorých prípadoch by sa určený tvar nemusel nachádzať v prehľadávanom obraze celý. Vyhľadávanie takýchto tvarov je možné vylúčiť zmenšením rozsahu parametrov. V prípade Obr. 3 boli pre obraz s rozlíšením 128×128 obrazových bodov použité nasledujúce parametre: ρ = {-180, -179, …, -1, 0, 1, …, 179, 180} a θ = {-90°, -89°, …, -1°, 0°, 1°, …, 89°, 90°}.

Posledný krok algoritmu pozostáva z výberu maxím akumulátora. Počet vybratých maxím je zvolený používateľom. Tvary, ktoré sú reprezentovanými maximami sa následne vykreslia. Príklad posledného kroku ukazujú Obr. 4 a Obr. 5. V tomto prípade bolo vybratých osem maxím, ktoré sú v akumulátore označené červenými krúžkami. Keďže jedno z maxím má príliš veľkú hodnotu polomeru ρ (približne -100), v obraze s detekovanými priamkami sa príslušná priamka nenachádza. Nízka vzdialenosť medzi maximami spôsobuje nízku vzdialenosť medzi nájdenými priamkami, prípadne ich rovnobežnosť (Obr. 5).

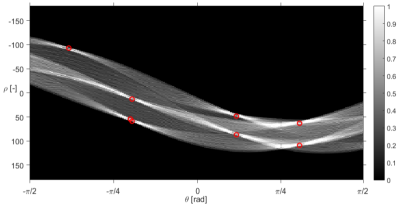
Obr. 4 Maximá vybraté z akumulátora

Obr. 5 Sedem priamok získaných Houghovou transformáciou

3. Praktický príklad

Jedným zo známych použití HT je aj detekcia dopravných značiek. V tomto prípade HT vyhľadáva priamky, ktoré ohraničujú plochy (trojuholníky, štvoruholníky, resp. osemuholníky), alebo kruhy. Pred použitím HT môžu byť vykonávané operácie, ktoré zo snímanej scény vyberajú určitý výrez (angl. ROI, Region of Interest). HT sa následne použije na určenie tvarov značiek. Po rozoznaní tvaru značky sa pokračuje v určení konkrétnej dopravnej značky porovnávaním s referenčnými značkami [9, 10]. Príklad rozoznania tvaru značky (trojuholník) ukazuje Obr. 6. Za povšimnutie stojí skutočnosť, že pri použití prahovej hodnoty šiestich priamok bol objavený nielen „vonkajší“, červený trojuholník, ale aj „vnútorný“, biely trojuholník značky. Farba trojuholníka však nie je dôležitá, pretože tvary sa rozpoznávajú na základe hrán obrazov v odtieňoch sivej (ako je možné vidieť na Obr. 1).

Obr. 6 Rozpoznanie tvaru dopravnej značky (trojuholník)

4. Záver

Tento článok sa venoval opisu algoritmu, ktorý slúži na rozpoznávanie tvarov, Houghovej transformácii (HT). Popísané sú aj jednotlivé kroky algoritmu, ako detekcia hrán, použitie polárnych súradníc, hlasovacia procedúra, výber maxím a vykreslenie tvarov. Okrem toho príspevok spomína aj použitie HT v oblasti rozpoznávania zvislých dopravných značiek. Pomerne jednoduchý algoritmus HT však pri detekcii zložitejších geometrických tvarov spôsobuje zvýšenú výpočtovú náročnosť. Pre jej zníženie je potrebné predpokladať miesto výskytu, prípadne rozmery a orientáciu (alebo rozsah parametrov) hľadaných tvarov. Kvôli týmto dôvodom je využitie HT v niektorých prípadoch (zložité scény) otázne.

S narastajúcim výkonom hardvérových zariadení je možné očakávať aj väčšie rozšírenie HT a aplikácií, ktoré napomáhajú vodičom. Okrem detekcie tvaru zvislého dopravného značenia, ktorý sa použije pri rozpoznaní konkrétnej značky, sa v dnešnej dobe rozpoznáva aj prechod medzi jazdnými pruhmi. V budúcnosti je možné uvažovať aj o rozpoznávaní vodorovného dopravného značenia. Problémom sú značky, resp. nápisy, ktoré nie je možné aproximovať súborom jednoducho parametrizovateľných tvarov.

Použitá literatúra

1. P. V. C. Hough, „Machine Analysis of Bubble Chamber Pictures,“ v Proceedings of Internatonal Conference on High-Energy Accelerators and Instrumentation, Geneva (Switzerland), 1959, s. 554–556.
2. R. O. Duda, P. E. Hart, „Use of the Hough Transformation To Detect Lines and Curves in Pictures,“ v Communications of the ACM, roč. 15, zv. 1, 1972, s. 11–15. ISSN: 0001-0782. DOI: 10.1145/361237.361242.
3. P. E. Hart, „How the Hough Transform Was Invented,“ v IEEE Signal Processing Magazine, roč. 26, zv. 6, 2009, s. 18–22. ISSN: 1053-5888. DOI: 10.1109/MSP.2009.934181.
4. J. Chmúrny, J. Turán, „Houghova transformácia parametrických kriviek a jej využitie pri spracovaní obrazov“ v Elektrotechnický časopis, roč. 38, zv. 6, 1987, s. 475–485.
5. D. H. Ballard, „Generalizing the Hough Transform to Detect Arbitrary Shapes,“ v Pattern Recognition, roč. 13, zv. 2, 1981, s. 111–122. ISSN: 0031-3203. DOI: 10.1016/0031-3203(81)90009-1.
6. Canny, „A Computational Approach to Edge Detection,“ v IEEE Transactions on Pattern Analysis and Machine Intelligence, roč. 8, zv. 6, 1986, s. 679–698. ISSN: 0162-8828. DOI: 10.1109/TPAMI.1986.4767851.
7. J. M. S. Prewitt, „Object Enhancement and Extraction,“ v Picture processing and Psychopictorics (editors B. S. Lipkin and A. Rosenfeld), Academic Press, New York, 1970, ISBN: 978-0-12-414367-8, 534 s.
8. I. Sobel, „An Isotropic 3×3 Image Gradient Operator,“ v Pattern Classification and Scene Analysis (editors R. Duda and P. Hart), John Wiley and Sons, New York, 1973, ISBN: 978-0-47-122361-0, s. 271–272.
9. M. Á. García-Garrido, M. Á. Sotelo, E. Martín-Gorostiza, „Fast Road Sign Detection Using Hough Transform for Assisted Driving of Road Vehicles,“ v Proceedings of EUROCAST 2005, Las Palmas (Spain), 2005, s. 543–548. ISBN: 978-3-54-031829-3.
10. D. Solus, Ľ. Ovseník, J. Turán, „Image Pre-processing in Vertical Traffic Signs Detection System,“ v Carpatian Journal of Electronic and Computer Engineering, roč. 8, zv. 1, 2015, s. 35–38. ISSN: 1844-9689.

---

Spoluautorom článku je doc. Ing. Ľuboš Ovseník, PhD., Katedra elektroniky a multimediálnych telekomunikácií, FEI TU Košice, Slovenská republika.