Stegoanalýza predstavuje účinný nástroj na detekciu podprahových kanálov, ktoré boli vytvorené ľubovoľným steganografickým algoritmom. V modernej stegoanalýze je základom pre vytvorenie účinného nástroja implementovanie strojového učenia sa. Najčastejšie sa používa metóda podporných vektorových strojov. V závislosti na množine extrahovaných štatistických parametrov dosahuje daná metóda v stegoanalýze relatívne vysokú účinnosť pri detekcii dobre známych, ale aj nových algoritmov. V tomto článku sú porovnané dva nastavenia metódy podporných vektorových strojov. Ide o voľbu kernelovej funkcie, ktorá slúži na transformáciu lineárne neseparovateľných parametrov do viacrozmerného priestoru. Testované boli lineárna kernelová funkcia a radiálna bázová kernelová funkcia. Prvá z dvojice dosiahla vyššiu úspešnosť detekcie, pričom druhá podstatne skrátila dobu trénovania klasifikátora.

1. Úvod do steganografie

Cieľom steganografie je ukryť tajnú informáciu do pozadia prenášaných dát, ktoré nevzbudzujú žiadne podozrenie. Takýto nosič prídavnej informácie môže byť akýkoľvek druh multimediálnych dát. Najčastejšie digitálny obraz, audio a video. Pred vložením tajnej informácie sa tieto dáta nazývajú krycie objekty, po vložení zasa stego objekty. Naproti steganografii stojí stegoanalýza. Stegoanalýza sa naopak zaoberá odhaľovaním takejto tajnej komunikácie vytvorenej steganografiou. Ak útočník vynakladá úsilie odhaliť vloženú tajnú informáciu v digitálnych obrazoch, hovoríme o obrazovej stegoanalýze. Jej proces začína extrakciou zvolených štatistických parametrov z obrazovej databázy. Následne sa za pomoci klasifikátora aplikuje strojové učenie sa a výsledkom je natrénovaný model. Ten sa využije pri analýze podozrivých obrazov. Konečným výsledkom je rozhodnutie, či sa tajná správa v danom obraze nachádza alebo nenachádza.

2. Univerzálna obrazová stegoanalýza

Podľa zamerania sa obrazová stegoanalýza triedi do dvoch základných skupín – cielená stegoanalýza a univerzálna stegoanalýza. Cielená stegoanalýza skúma konkrétny steganografický algoritmus a na základe výsledkov zvolí tie štatistické parametre, ktoré daná metóda ovplyvňuje. Zameriava sa teda na detekciu použitia jednej konkrétnej metódy. Na druhej strane, v univerzálnej steganografii sú vybrané tie štatistické parametre, ktoré sú ovplyvňované väčšinou steganografických algoritmov. V tejto práci je použitý systém univerzálnej stegoanalýzy. Konkrétna množina použitých štatistických parametrov je detailne popísaná v [1].

Štatistické parametre je možné extrahovať z viacerých oblastí. Najčastejšie priestorovej, oblasti po DCT (diskrétnej kosínusovej transformácii) a DWT (diskrétnej waveletovej transformácii). Ak sú štatistiky vypočítané práve z oblasti po DCT (konkrétne oblasť JPEG), jedná sa o stegoanalýzu na báze kalibrácie štatistík (features based steganalysis) [2]. Dôležitý element tohto typu stegoanalýzy je kalibrácia. Proces kalibrácie má za úlohu vytvoriť z testovaného obrazu obraz podobný kryciemu (obraz pred vložením tajnej správy). Nezáleží na tom, či sa v obraze nachádzala tajná správa alebo nie. Porovnávacím parametrom je množina štatistických parametrov, s ktorou daný systém pracuje. Kalibrácia sa začína dekompresiou obrazu z JPEG oblasti do priestorovej. Nasleduje orezaním 4 obrazových prvkov v každom smere a končí opätovnou kompresiou s rovnakým faktorom kvality. Získaný obraz sa nazýva kalibrovaný. Štatistické parametre sa vypočítajú z pôvodného aj kalibrovaného obrazu, odčítajú sa a výsledok putuje do klasifikátora. Takýto proces zabezpečí zníženie dynamického rozsahu hodnôt štatistických parametrov a teda aj skrátenie doby trénovania.

2.1. Metóda podporných vektorových strojov

Vo fáze trénovania klasifikátor vypočíta parametre separačnej hyperroviny, ktorá slúži na oddelenie štatistík patriacich krycím obrazom od štatistík stego obrazov. Táto hyperrovina sa následne použije na klasifikáciu štatistík extrahovaných z testovaného obrazu (Obr.1). V praxi sa používa viacero klasifikátorov, pričom najčastejšie je to SVM klasifikátor [3], celým názvom metóda podporných vektorových strojov (SVM-Support Vector Machine). SVM klasifikátor je vhodný na klasifikáciu lineárne separovateľných aj lineárne neseparovateľných problémov. Lineárne separovateľný problém je ilustrovaný na Obr.1. Ako už bolo spomenuté vyššie, klasifikátor v takomto prípade vypočíta parametre separačnej hyperroviny na základe vstupných štatistík patriacich k obom triedam. Pri testovaní klasifikátor použije túto hranicu na zobrazenie testovaných štatistík v príslušnej triede.

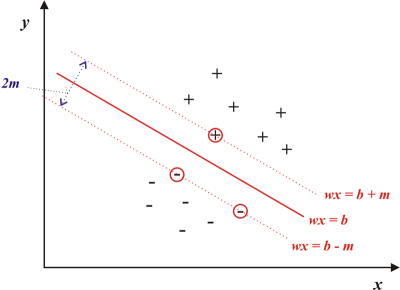
Obr.1 Lineárne separovateľný problém. Štatistiky v krúžku predstavujú podporné vektory, ktoré definujú optimálnu pozíciu separačnej hyperroviny.

Optimálna separačná hyperrovina je definovaná rovnicou (1) [4], kde x reprezentuje vstupný vektor, w vektor váhových koeficientov a b prahovú hodnotu. Hyperrovina je situovaná v strede rozsahu 2m, daného podpornými vektormi.

(1)

(2)

Ak je problém lineárne neseparovateľný, znamená to, že extrahované štatistiky nie je možné separovať v 2D priestore. V takomto prípade sú štatistiky transformované do priestoru s väčším počtom dimenzií. Táto transformácia zabezpečí to, že problém sa stane lineárne separovateľný v novom priestore. Transformácia do priestoru s vyšším rozmerom je zobrazená na Obr.2.

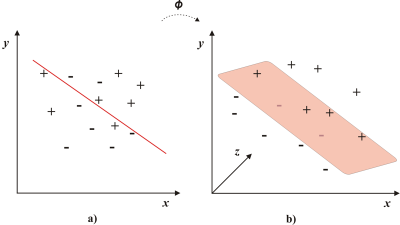
Obr.2 a) Lineárne neseparovateľný problém. b) Transformácia do viac-rozmerného priestoru

Ak vstupný vektor označíme x, jeho transformácia bude Φ(x). Separačná hyperrovina je v takom prípade definovaná rovnicou (2). Funkcia, ktorá zabezpečuje transformáciu sa nazýva kernelová funkcia.

3. Výsledky experimentov

Obrazová databáza pozostávala z prirodzených statických obrazov zachytených rôznymi druhmi fotoaparátov. Obrazy majú rôzne rozlíšenie, detaily a boli zachytené pri rôznych svetelných podmienkach. Konkrétny popis použitej databázy obrazov sa nachádza v [5].

Databáza stego obrazov bola vytvorená za pomoci štyroch steganografických metód – nsF5, MHF-DZ [6], MB2 a PQ. S cieľom vytvorenia efektívnejšieho nástroja stegoanalýzy boli vkladané správy s rôznou veľkosťou. Vo fáze trénovania boli vytvorené tieto modely pre binárnu klasifikáciu – model krycie obrazy – nsF5 stego obrazy, krycie obrazy – MHF-DZ stego obrazy, krycie obrazy – MB2 stego obrazy a krycie obrazy – PQ stego obrazy. Tieto modely boli trénované na obrazovej databáze z 4000 krycích a stego obrazov použitím SVM klasifikátora (libsvm [7]). Klasifikátor SVM využíval dva typy kernelovej funkcie, lineárnu kernelovú funkciu (L-SVM) a radiálnu bázovú kernelovú funkciu (R-SVM). Pre parameter c sme zvolili hľadaný interval <-5,-3>. Ostatné parametre sme ponechali v základnom režime. Merania boli vykonané za pomoci procesora Intel Core Duo E6750 s taktovacou frekvenciou 2,66 GHz.

Tabuľka 1 zobrazuje metriku Accuracy (ACR) pre detekciu 4 steganografických algoritmov s troma veľkosťami správ (payload) za pomoci oboch typov kernelových funkcií. Payload 100% znamená využitie maximálnej kapacity média pre konkrétnu steganografickú metódu. Z tabuľky aj Obr.3 vyplýva, že pre každú z metód dosiahol lepšiu detekciu klasifikátor L-SVM. Avšak ACR pre modely krycie obrazy – MB2 stego obrazy a krycie obrazy – PQ stego obrazy nebol menší ako 0,7 pre oba klasifikátory.

Tab.1 Accuracy (ACR) natrénovaných modelov pomocou L-SVM a R-SVM klasifikátorov pre detekciu rôznych steganografických algoritmov a veľkostí správ.

Testovaný algoritmus	Payload	L-SVM	R-SVM
ACR	ACR
nsF5	25%	0,74	0,64
	50%	0,9	0,81
	100%	0,93	0,87
MHF-DZ	25%	0,68	0,63
	50%	0,7	0,64
	100%	0,79	0,67
MB2	25%	0,82	0,75
	50%	0,86	0,77
	100%	0,9	0,86
PQ	25%	0,98	0,94
	50%	0,97	0,96
	100%	0,96	0,95

Priemerná presnosť detekcie oboch klasifikátorov je zobrazená na Obr.3. V tomto prípade bolo testovaných 8 veľkostí tajných správ. Výsledky sú podobné ako v predchádzajúcom experimente. L-SVM dosiahol vyššiu hodnotu ACR pre detekciu všetkých steganografických metód.

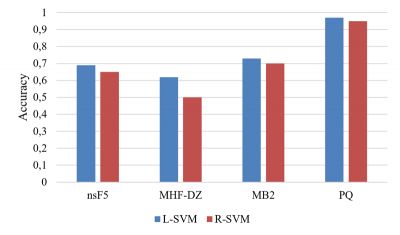
Obr.3 Priemerná presnosť detekcie dosiahnutá klasifikátormi L-SVM a R-SVM

Na druhej strane, výhoda klasifikátora R-SVM spočívala v dobe natrénovania modelu.

Tab.2 Doba trénovania v závislosti na veľkosti obrazovej databázy.

Ntrn	L-SVM	R-SVM
1000	1 m	< 10 s
2000	6,5 m	30 s
4000	30 m	3 m
8000	2 h	10 m
12000	4,5 h	< 30 m

Ako je vidieť v Tab.2, doba trénovania modelu s 1000 obrazmi trvala približne 1 min pre L-SVM a menej ako 10 sekúnd pre R-SVM. Tento rozdiel je však viac viditeľný pre množinu s 12000 obrazmi, kde L-SVM natrénoval model za 4,5 hodiny, pričom klasifikátor s radiálnou bázovou kernelovou funkciou to zvládol za menej ako 30 min.

3. Záver

Presnosť detekcie v stegoanalýze závisí aj od typu kernelovej funkcie. Klasifikátor SVM s lineárnou kernelovou funkciou dosiahol vyššiu efektivitu ako s radiálnou bázovou kernelovou funkciou pre detekciu všetkých štyroch typov steganografických nástrojov využívaných v tejto práci. Avšak pre tri steganografické algoritmy bola hodnota parametra ACR klasifikátora R-SVM len o 0,06 menšia v porovnaní s detekciou L-SVM. Navyše, doba trénovania bola značne kratšia v prospech R-SVM, čo by mohlo priniesť výhodu pri vytváraní modelu s veľkou vstupnou obrazovou databázou. Nastavenie klasifikátora má veľký vplyv na jeho výslednú efektivitu, a preto by bolo v ďalšom výskume vhodné otestovať viacero kombinácií a nastavení nielen kernelovej funkcie, ale aj jeho ostatných parametrov.

4. Poďakovanie

Táto publikácia vznikla vďaka podpore v rámci operačného programu Výskum a vývoj pre projekt “(Rozvoj Centra informačných a komunikačných technológií pre znalostné systémy) (kód ITMS:26220120030), spolufinancovaný zo zdrojov Európskeho fondu regionálneho rozvoja“.

Literatúra

1. PEVNÝ, T., FRIDRICH, J. Merging Markov and DCT Features for Multi-Class JPEG Steganalysis, in E. J. Delp and P. W. Wong, editors, Proceedings SPIE, Electronic Imaging, Security, Steganography, and Watermarking of Multimedia Contents IX, CA: San Jose, 2007, vol. 6505, pp. 31-34.
2. FRIDRICH, J. Feature-based steganalysis for jpeg images and its implications for future design of steganographic schemes, in Proc. 6th Information Hiding Workshop, Toronto, 2004.
3. VAPNIK, V. The Nature of Statistical Learning Theory, Springer: New York, 1995.
4. BENNETT, K.P., BLUE, J.A. A Support Vector Machine Approach to Decision Trees, Neural Net-works Proceedings, 1998. IEEE World Congress on Computational Intelligence. The 1998 IEEE International Joint Conference on, vol. 3, May 1988, pp. 2396-2401 vol.3, pp. 4-9.
5. BRODA, M., HAJDUK, V., LEVICKÝ, D. The Comparison of Classifiers in Image Steganalysis, Acta Electrotechnika et Informatica, FEI-TU: Košice, 2014, vol. 14, no. 4, pp. 1-4, ISSN 1335-8243.
6. BÁNOCI, V., a kol., A Novel JPEG Steganography Method Based on Modulus Function with Histogram Analysis, in: Radioengineering, 2012, vol. 21, no. 2, pp. 758-763, ISSN 1210-2512.
7. CHANG, C.C., LIN, C.J. LIBSVM: a library for support vector machines, 2001, available at
   http://www.csie.ntu.edu.tw/~cjlin/libsvm/

---

Spoluautorom článku je prof. Ing. Dušan Levický, CSc., Laboratórium progresívnych komunikačných technológií, Katedra elektroniky a multimediálnych telekomunikácií, Fakulta elektrotechniky a informatiky, Technická univerzita v Košiciach.