Problém energie a spracovania ropy v Popolvárovom kráľovstve II.

07. Október, 2009, Autor článku: Benko Ján, Prírodné vedy
Ročník 2, číslo 10 This page as PDF Pridať príspevok

ropny_vrtV predchádzajúcej časti sa Jakub vybral hľadať nové zdroje energie, pričom za pomoci starenky našie ropu. Na pomoc si zavolal Popolvára s Dedom Vševedom, ktorý mu mali pomôcť so spracovaním objavením ropy. Spolu vyvinuli zariadenie na frakčnú destiláciu ropy. Na základe Popolvárových experimentov Dedo Vševedo, začal pracovať na teoretickom výpočte počtu poschodí v destilačnej kolóne, aby sa dosiahla potrebná čistota jednotlivých frakcií.

Najprv sa zaoberal rovnováhou medzi čistou kvapalinou – parou. Podmienkou termodynamickej rovnováhy je rovnosť chemických potenciálov oboch fáz. Z tejto podmienky odvodil vzťah, ktorý vyjadruje závislosť tlaku nasýtených pár od teploty, rovnica (1). Neskôr túto rovnicu odvodili Clausius a Clapeyron, podľa ktorých dostala meno.

\frac{d \ln P}{dT} = \frac{ \Delta H_{vyp}}{R T^2} (1)

kde \Delta H_{vyp} je výparné teplo kvapaliny, P je tlak a T je teplota v K.

Po integrácii dostaneme vzťah (2)

\ln P= - \frac{ \Delta H_{vyp}}{R T} + C (2)

kde C je integračná konštanta. Závislosť bodu varu od teploty pre n-hexán a n-heptán nameral Popolvár, tabuľka 1.

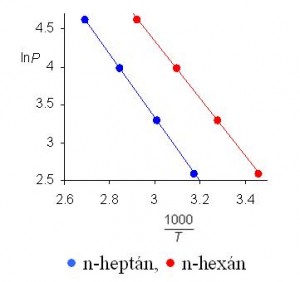
Zo závislosti \ln P = f(1/T) , obr. 3, vypočítal hodnoty výparného tepla a integračnej konštanty. Závislosť tlaku nasýtených pár od teploty vyjadrujú rovnice (3) pre n-hexán a (4) pre n-heptán. Z týchto rovníc sa dá pre danú teplotu vypočítať tlak nasýtených pár, alebo bod varu pri danom tlaku.

\ln P= - \frac{31500}{R T} + 22.607 (3)

\ln P= - \frac{34868}{R T} + 22.812 (4)

T/K
P/Pa n-hexán n-heptán
101300 341.90 371.60
53320 322.80 351.20
26650 304.80 331.90
13330 289.00 315.00

Tabuľka 1 Teploty varu pri rôznych tlakoch pre n-hexán a n-heptán


popol3
Obr. 3. Závislosť \ln P = f(1000/T)

N-heptán a n-hexán sú neobmedzene miešateľné kvapaliny. Dedo Vševedo predpokladal, že sa chovajú ideálne, interakcie medzi n-heptánom a n-hexánom považoval za rovnaké ako interakcie n-hexán – n-hexán a n-heptán – n-heptán. Parciálny tlak jednotlivých zložiek nad ich kvapalnou zmesou je daný vzťahmi (5) a (6), (Dedo Vševedo opäť nepublikoval svoje výsledky. Neskôr, nezávisle na ňom, k tým istým záverom sa dopracoval Raoult, dnes sú známe pod názvom Raoultov zákon).

P_{1} = P _{1} ^{o} x_1 (5)

P_{2} = P _{2} ^{o} x_2 (6)

Kde P1, P2 sú parciálne tlaky zložiek 1 a 2 nad kvapalnou zmesou, x1 a x2sú mólové zlomky látok v kvapalnom stave P_{1} ^{o} a P_{2} ^{o} sú tlaky nasýtených pár pre čistú zložku (pre náš prípad označíme n-hexán indexom 1 a n-heptán indexom 2).

Celkový tlak nasýtených pár nad zmesou kvapalín je daný súčtom ich parciálnych tlakov (Daltonov zákon), rovnica (7).

P = P_{1} ^{o} * x_{1} + P_{2} ^{o} * x_{2} = P_{1} ^{o} * x_{1} + P_{2} ^{o} (1 - x_{1}) = x_{1} (P_{1} ^{o} - P_{2} ^{o}) +P_{2} ^{o} (7)

kde koncentrácia je x_{2} = 1 - x_{1}

Závislosť celkového tlaku od zloženia, vyjadreného v molových zlomkoch, je lineárna. Nakoľko je počet molov zložky v plynnej fáze, pri konštantnom objeme, úmerný jej tlaku možno napísať rovnicu (8)

n_{1} : n_{2} = y_{1} : y_{2} = P_{1} : P_{2} = P_{1} ^{o}* x_{1} : P_{2} ^{o}* x_{2} (8)

kde y1 a y2 sú mólové zlomky oboch zložiek v plynnej fáze.

Úpravou rovníc (7) a (8) dostaneme rovnice (9) a (10), ktoré vyjadrujú závislosť zloženie plynnej fázy od zloženia kvapalnej fázy.

y_{1} = \frac{P _{1} ^{o} x_{1}}{P _{2} ^{o} + (P _{1} ^{o} - P _{2} ^{o})x_{1}} (9)

y_{2} = \frac{P _{2} ^{o} x_{2}}{P _{2} ^{o} + (P _{21} ^{o} - P _{1} ^{o})x_{2}} (10)

Aby sme mohli zostrojiť izobarický fázový diagram potrebujeme vypočítať body varu pri konštantnom tlaku pre rôzne pomery n-hexánu a n-heptánu. Zvolíme si určitý počet teplôt medzi bodmi varu čistých zložiek oboch kvapalín a pre každú vypočítame tlak nasýtených pár oboch zložiek, vzťahy (3) a (4). Pre každú teplotu vypočítame zo vzťahov (7), (9) a (10) zákona príslušné zloženie kvapalnej aj plynnej fázy. Výsledkom je izobarický fázový diagram na obr. 4.

popol4
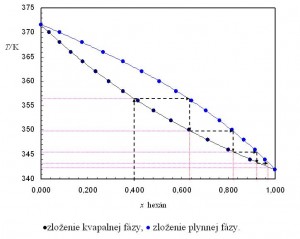
Obr. 4 Izobarický fázový diagram. Závislosť bodu varu zmesi n-hexán – n-heptán od zloženia

Ak poznáme zloženie kvapalnej fázy, môžeme z grafu odčítať jeho bod varu a tiež zloženie plynnej fázy. Ako vidno z fázového diagramu plynná fáza je obohatená o prchavejšiu zložkou, n-hexán. Po jej skondenzovaní dostaneme kvapalnú fázu obohatenú o túto zložku. Kondenzát opäť privedieme do varu a opäť necháme skondenzovať, takto postupne oddelíme obe zložky od seba. Pomocou fázového diagramu môžeme odhadnúť počet poschodí frakčnej kolóny ak chceme dostať výslednú látku určitej čistoty. Presnejšie to môžeme urobiť výpočtom. Pomocou programu EXCEL sa našiel polynóm, vyjadrujúci závislosť bodu varu zmesi od zloženia, vzťah (11).

T = -6.5510 x^{3} + 22.7731 x^{2} - 45.9136 x + 371.5678 (11)

Uvažujme, že máme počiatočnú koncentráciu zmesi x(n-hexán)=0.4 Z rovnice (11) vypočítame bod varu zmesi. Pomocou rovníc (7), (9) a (10) vypočítame príslušné tlaky nasýtených pár a zloženie plynnej fázy. Toto zloženie považujeme za východiskové v druhom stupni destilácie, takto postupujeme, kým nedostaneme požadovanú čistotu kondenzátu. Ak chceme dosiahnuť obsah n-hexánu 99.9% potrebujeme kolónu s minimálne ôsmimi poschodiami. Situáciu na jednotlivých poschodiach vyjadruje tabuľka 2.

Vzťah (9) môžeme zjednodušiť zavedením relatívnej prchavosti (reparačného faktora) \alpha = \frac{P _{1} ^{o}}{P _{2} ^{o}} . Reparačný faktor je pre mnohé zmesi približne konštantný, (tabuľka 3). Ak Platí Raoultov zákon, pomery na prvom poschodí kolóny možno vyjadriť vzťahom (12)

\frac{P_{1}}{P_{2}} = \frac{x'_{1}}{x'_{2}} = \frac{y'_{1}}{y'_{2}} = \frac{P_{1} ^{o} x_{1}}{P_{2} ^{o} x_{2}} = \alpha \frac{x_{1}}{x_{2}} (12)

kde x'_{1} a x'_{2} sú koncentrácie zložiek v prvom kondenzáte

Po druhej destilácii platí pre zloženie destilátu vzťah (13)

\frac{P''_{1}}{P''_{2}} = \frac{x''_{1}}{x''_{2}} = \frac{y''_{1}}{y''_{2}} = \frac{P_{1} ^{o} x'_{1}}{P_{2} ^{o} x'_{2}} = \alpha ^{2} \frac{x_{1}}{x_{2}} (13)

Pre n destilácií pre teoretický počet poschodí platí vzťah (14)

\frac{y_{1}}{y_{2}} = \alpha ^{n} \frac{x_{1}}{x_2} (14)

Ak dosadíme do rovnice (14) za \frac{y_{1}}{y_{2}} = \frac{0.999}{0.001} , za \frac{x_{1}}{x_{2}} = \frac{0.4}{0.6} a priemernú hodnotu \alpha = 2.629 dostaneme pre počet poschodí hodnotu

n = \frac{ \log ( \frac{0.999 * 0.6}{0.001 * 0.4} )}{ \log 2.629} = 7.54 \approx 8
poschodie č. x – heptán T/K – varu P Pa – hexán P Pa – heptán y – hexán α
1. 0.4 356.4 159137 62661 0.629 2.540
2. 0.629 350.1 131191 50601 0.815 2.593
3. 0.815 345.7 114525 43536 0.92 2.631
4. 0.92 343.5 106660 40239 0.968 2.651
5. 0.968 342.5 103347 38857 0.988 2.660
6. 0.988 342.1 101953 38278 0.996 2.664
7. 0.996 341.9 101459 38072 0.999 2.665
8. 0.999

Tabuľka 2 Hodnoty zloženia, teploty varu, parciálnych tlakov a koeficientu a na jednotlivých poschodiach destilačnej kolóny

Napísať príspevok