Robust SISO control design for thermo-optical plant UDAQ28/LT

29. Máj, 2008, Autor článku: Osuský Jakub, Elektrotechnika, Študentské práce
Ročník 1, číslo 5 Pridať príspevok

In this paper design of robust control for thermo-optical plant uDAQ28/LT is presented. SISO controllers for temperature and light intensity control were designed. For modeling real and complex perturbation input multiplicative uncertainty was applied and robust stability condition was derived in terms of the M-delta structure.

INTRODUCTION

A control system is robust if it is insensitive to differences between the actual system and the system model used to design the controller. These differences are referred to as model/plant mismatch or simply model uncertainty. Uncertainty in the system model may have several sources: imperfect measuring devices, variations of the linear model parameters due to nonlinearities or changes in the operating conditions, only approximate knowledge of some parameters etc. To deal with it the uncertainty model is used [1, 3]; then, instead of examining a single plant model, the behavior of a class of models is considered. Let $\tilde {G}(s)\in \Pi$ be any member of a set of possible plants $\Pi$ and $\tilde {G}_{0}(s)\in \Pi$ be the nominal model of the plant. A simple uncertainty model is obtained using unstructured uncertainty, i.e. a perturbation $\Delta$ satisfying $|\Delta (j\omega )|\leqslant 1$ .

This paper deals with modeling of uncertain plants in frequency domain. Input multiplicative uncertainty is applied to allow robust stability analysis and conditions guaranteeing stability of the uncertain plant for all perturbations in the uncertainty set are derived using the Generalized Nyquist stability theorem and the $M-\Delta$ structure stability conditions.

PRELIMINARIES AND PROBLEM FORMULATION

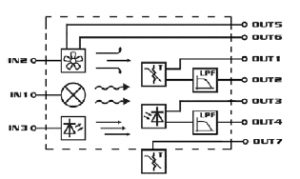
Thermo-optical plant uDAQ28/LT (Fig. 1) is multivariable system with three manipulated inputs and seven measurable outputs (Fig. 2).

Fig. 1 Thermal plantuDAQ28/LT

Fig.2 Basic electric diagram of thermo-optical plant uDAQ28/LT

System has three manipulated inputs: bulb voltage (0-5V) which represents heater and light source, fan voltage (0-5V) which can be used for temperature decreasing and voltage of led diode (0-5V) which represents another source of light.

On the output is possible to measure seven variables: temperature insight the system (direct or filtrated), outsight temperature, light intensity (direct or filtrated), fan velocity and fan current.

Problem formulation:

Design two PID controllers which will guarantee closed-loop robust stability within the uncertainty range specified by the given working points. One for light intensity and one for temperature control.

THEORETICAL RESULTS

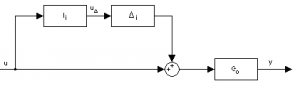
Consider the uncertain plant modeled using the input multiplicative form of uncertainty (Fig. 5)

Fig. 3 Input multiplicative uncertainty

According to Fig. 3, the uncertain plant is described as follows:

$\tilde {G}=G_{0}(1-l_{i}\Delta _{i})$ with $|\Delta_{i} (j\omega )|\leqslant 1$

(1)

Rule for computing the corresponding weighting function as follows:

$l_{i}(\omega )=\underset{\tilde {G}\in \Pi }{\mathit{max}}[G_{0}^{-1}(G_{0}-\tilde {G})]$

(2)

The set of perturbed plants is given as a set of transfer functions $G_{k},k=1,2, \ldots ,N$ identified in N different working points. In such case (4) modifies to

$l_{i}(\omega)=\underset{k}{\mathit{max}}[G_{0}^{-1}(G_{0}-G_{k})] \qquad k=1,2, \ldots , N$

(3)

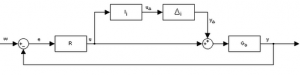
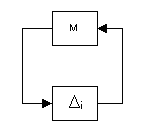
To derive the related robust stability condition, the feedback system with the input multiplicative uncertainty in Fig. 4 is to be transformed into the $M-\Delta$ structure (Fig. 5) and the robust stability theorem [1] is to be applied.

Fig. 4 Feedback system with the input multiplicative uncertainty

Fig. 5 $M-\Delta$ structure

Theorem 1 (Robust stability for unstructured perturbations)

Assume that the nominal system M(s) is stable and the perturbation $\Delta _{i}(s)$ is stable. Then the $M-\Delta_{i}$ system in Fig. 5 is stable for all perturbations satisfying $|\Delta (j\omega )|\leqslant 1$ if and only if $|M(j\omega )|\leqslant 1$ $\forall \omega$ .

For the input multiplicative uncertainty case M is computed as follows:

$lM=l_{i}\mathit{RG}_{0}(1+G_{0}R)^{-1}=l_{i}M_{0}$

(4)

and

$M_{0}=\mathit{RG}_{0}(1+G_{0}R)^{-1}$

(5)

According to the Theorem 1 the robust stability condition $|M(j\omega )|\leqslant 1$ modifies to

$\mid M_{0} (j\omega ) \mid < \frac{1}{\mid l_{i}(\omega ) \mid} [/latex]</td> <td style="width:20px; text-align:center;">(6)</td> </tr> </table> Relations (3), (5) and (6) will be applied in the design of a robust controller for thermo-optical plant uDAQ28/LT. CASE STUDIES In both cases when light intensity a temperature will be controlled, bulb voltage as a manipulated input will be used because it is dominant input for both controlled variables. In first step static characteristics will be measured and working points chosen. <a href="http://www.posterus.sk/wp-content/uploads/p41_06_fig6.png"><img src="http://www.posterus.sk/wp-content/uploads/p41_06_fig6-300x124.png" alt="" title="p41_06_fig6" width="300" height="124" class="alignleft size-medium wp-image-6183" /></a> Fig.6 Static characteristic for light intensity and temperature The system for temperature control will be identified in three working points WP1 (42), WP2 (36.5) and WP3 (39.5) WP (temperature) 1st working point: <table style="width:100%;"> <tr> <td style="text-align:center;"><img src='https://s0.wp.com/latex.php?latex&bg=ffffff&fg=000000&s=0' alt='' title='' class='latex' />G_{1}(s)=\frac{4.543s+5.357}{7,14s_{2}+216.357s+1}$

(7)

2nd working point:

$G_{2}(s)=\frac{9.577s+5.339}{7,692s_{2}+358.615s+1}$

(8)

3rd working point:

$G_{3}(s)=\frac{7.78s+5.002}{5.903s_{2}+241.588s+1}$

(9)

and similar system for light intensity control will be identified in three working points too. WP1 (16), WP2 (5.5) and WP3 (10)

1st working point:

$G_{1}(s)=\frac{-2.7s+10.93}{0.775s_{2}+21.434s+1}$

(10)

2nd working point:

$G_{2}(s)=\frac{-3.137s+10.25}{0.392s_{2}+21.349s+1}$

(11)

3rd working point:

$G_{3}(s)=\frac{-1.152s+10.616}{1.505s_{2}+30.489s+1}$

(12)

For these three working points the mean value parameter nominal model will be calculated.

Nominal model for temperature control

$G_{0}(s)=\frac{7.3s+5.233}{6.912s_{2}+272.2s+1}$

(13)

and for light intensity control.

$G_{0}(s)=\frac{-2.33s+10.6}{0.891s_{2}+24.42s+1}$

(14)

The uncertainty weight functions for temperature and light intensity computed according to (3) are plotted in Fig. 7.

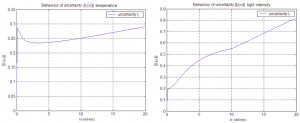
Fig. 7 weighting functions for the input multiplicative uncertainty: $l_{i}\ \mathit{versus}\ \omega$ plot

For the nominal model controllers $R(s)=k+\frac{k_{i}}{s}+k_{d}s$ will be designed using parameterization method [2].

$R_{temp}(s)=2.8+\frac{0.1}{s}+0.07s$

(15)

$R_{light}(s)=0.79+\frac{0.0323}{s}+0.0288s$

(16)

Nominal closed-loop stability has been verified by calculating roots of the closed-loop characteristic polynomial $1+G_{0}(s)R(s)=0$ ; the resulting set $\Lambda$ of closed-loop roots proves the nominal stability.

$\Lambda _{\mathit{temp}}=\{-39.4168,-0.0280,\pm 0.0317i\}$

(17)

$\Lambda _{\mathit{light}}=\{-39.5082,-0.0172,\pm 0.0312i\}$

(18)

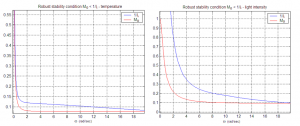
Robust stability condition (6) is verified in Fig. 8. Indeed, the blue line corresponding to $|M_{0}(j\omega )|$ lies below the red line corresponding to $\frac{1}{l_{i}(\omega )}$ over the whole frequency range considered. Robust stability has been verified also by simulations (Fig. 14-18).

Fig. 8 Verification of the robust stability conditions $|M_{0}(j\omega )|<\frac{1}{|l_{i}(\omega )|}$

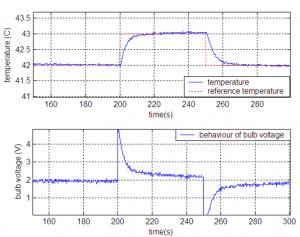
Fig.9 Step response for temperature in WP1

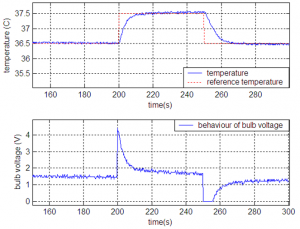
Fig.10 Step response for temperature in WP2

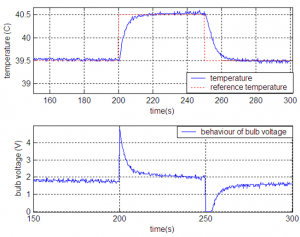
Fig.11 Step response for temperature in WP3

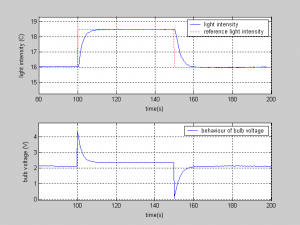
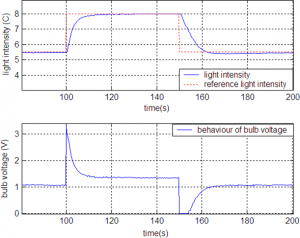
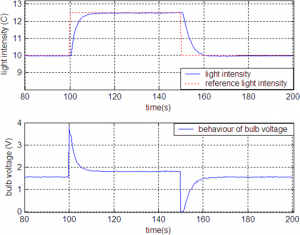
Fig.12 Step response for light intensity in WP1

Fig.13 Step response for light intensity in WP2

Fig.14 Step response for light intensity in WP3

Simulations proved that system is stable in all working points. Step responses for both outputs (light intensity and temperature) are practically without any overshot.

5 CONCLUSIONS

In this paper design of robust control for thermo-optical plant uDAQ28/LT was presented. For modeling real and complex perturbation input multiplicative uncertainty was applied. Robust stability conditions guaranteeing stability of the whole set of uncertain plants were derived. Theoretical results have been verified by simulations directly on thermo-optical plant uDAQ28/LT.

Acknowledgments

The work on this paper has been supported by the ESF Project No. 13120200115.

REFERENCES

Skogestad, S., I. Postlethwaite: Multivariable Feedback Control: Analysis and Design. John Wiley and Sons, 1996.
Kozáková, A. and V. Veselý: Independent design of decentralized controllers for specified closed-loop performance. In: /European Control Conference ECC´03/, Cambridge, UK, 2003

Napísať príspevok

Rubriky

Category Order could not understand your category HTML. Please do the following:

Disable all plugins except for category order to see if some other plugin is causing the problem. If the problem goes away, re-enable each plugin until you find the incompatible one.
Try switching to a different theme, like the WordPress default theme.

Once you have tried the above steps, email david@coppit.org with the results of these debugging steps. Also include the following information:

Original HTML:
<li class="cat-item cat-item-34"><a href="https://www.posterus.sk/?cat=34" >Elektrotechnika</a>
</li>
<li class="cat-item cat-item-54"><a href="https://www.posterus.sk/?cat=54" >Humanitné vedy</a>
</li>
<li class="cat-item cat-item-6"><a href="https://www.posterus.sk/?cat=6" >Informácie pre autorov</a>
</li>
<li class="cat-item cat-item-15"><a href="https://www.posterus.sk/?cat=15" >Informačné technológie</a>
</li>
<li class="cat-item cat-item-7"><a href="https://www.posterus.sk/?cat=7" >MATLAB/Comsol</a>
</li>
<li class="cat-item cat-item-17"><a href="https://www.posterus.sk/?cat=17" >Medicína</a>
</li>
<li class="cat-item cat-item-1"><a href="https://www.posterus.sk/?cat=1" >Nezaradené</a>
</li>
<li class="cat-item cat-item-5"><a href="https://www.posterus.sk/?cat=5" >O webe</a>
</li>
<li class="cat-item cat-item-36"><a href="https://www.posterus.sk/?cat=36" >Oznamy</a>
</li>
<li class="cat-item cat-item-22"><a href="https://www.posterus.sk/?cat=22" >Prírodné vedy</a>
</li>
<li class="cat-item cat-item-23"><a href="https://www.posterus.sk/?cat=23" >Strojárstvo</a>
</li>
<li class="cat-item cat-item-35"><a href="https://www.posterus.sk/?cat=35" >Študentské práce</a>
</li>

Processed HTML:
<li class="cat-item cat-item-34"><a href="https://www.posterus.sk/?cat=34" >Elektrotechnika</a>
</li>
<li class="cat-item cat-item-54"><a href="https://www.posterus.sk/?cat=54" >Humanitné vedy</a>
</li>
<li class="cat-item cat-item-6"><a href="https://www.posterus.sk/?cat=6" >Informácie pre autorov</a>
</li>
<li class="cat-item cat-item-15"><a href="https://www.posterus.sk/?cat=15" >Informačné technológie</a>
</li>
<li class="cat-item cat-item-7"><a href="https://www.posterus.sk/?cat=7" >MATLAB/Comsol</a>
</li>
<li class="cat-item cat-item-17"><a href="https://www.posterus.sk/?cat=17" >Medicína</a>
</li>
<li class="cat-item cat-item-1"><a href="https://www.posterus.sk/?cat=1" >Nezaradené</a>
</li>
<li class="cat-item cat-item-5"><a href="https://www.posterus.sk/?cat=5" >O webe</a>
</li>
<li class="cat-item cat-item-36"><a href="https://www.posterus.sk/?cat=36" >Oznamy</a>
</li>
<li class="cat-item cat-item-22"><a href="https://www.posterus.sk/?cat=22" >Prírodné vedy</a>
</li>
<li class="cat-item cat-item-23"><a href="https://www.posterus.sk/?cat=23" >Strojárstvo</a>
</li>
<li class="cat-item cat-item-35"><a href="https://www.posterus.sk/?cat=35" >Študentské práce</a>
</li>

Category pattern:
/http\:\/\/www\.posterus\.sk\/\?cat\=(\d+)/

Items:
Array
(
 [0] => <li class="cat-item cat-item-34"><a href="https://www.posterus.sk/?cat=34" >Elektrotechnika</a> </li>
 [1] => <li class="cat-item cat-item-54"><a href="https://www.posterus.sk/?cat=54" >Humanitné vedy</a> </li>
 [2] => <li class="cat-item cat-item-6"><a href="https://www.posterus.sk/?cat=6" >Informácie pre autorov</a> </li>
 [3] => <li class="cat-item cat-item-15"><a href="https://www.posterus.sk/?cat=15" >Informačné technológie</a> </li>
 [4] => <li class="cat-item cat-item-7"><a href="https://www.posterus.sk/?cat=7" >MATLAB/Comsol</a> </li>
 [5] => <li class="cat-item cat-item-17"><a href="https://www.posterus.sk/?cat=17" >Medicína</a> </li>
 [6] => <li class="cat-item cat-item-1"><a href="https://www.posterus.sk/?cat=1" >Nezaradené</a> </li>
 [7] => <li class="cat-item cat-item-5"><a href="https://www.posterus.sk/?cat=5" >O webe</a> </li>
 [8] => <li class="cat-item cat-item-36"><a href="https://www.posterus.sk/?cat=36" >Oznamy</a> </li>
 [9] => <li class="cat-item cat-item-22"><a href="https://www.posterus.sk/?cat=22" >Prírodné vedy</a> </li>
 [10] => <li class="cat-item cat-item-23"><a href="https://www.posterus.sk/?cat=23" >Strojárstvo</a> </li>
 [11] => <li class="cat-item cat-item-35"><a href="https://www.posterus.sk/?cat=35" >Študentské práce</a> </li>
)