Ako Popoluška prekabátila Martinka Klingáča – riešenie

17. August, 2009, Autor článku: Benko Ján, Prírodné vedy
Ročník 2, číslo 8 This page as PDF Pridať príspevok

V predošlej časti zajal zákerný Martinko Klingáč Popolušku a nechal ju riešiť úlohu a zobral jej baterky z kalkulačky. Myslel si že úlohu nevyrieši ale prerátal sa. Popoluška si vyrobila galvanický článok z jabĺčok a drôtikov a úlohu hravo vyriešila.

Tu je riešenie Popoluškinej úlohy:

pH roztoku je definované ako záporný logaritmus aktivity H3O+ iónov, rovnica (1)

pH = - \log a_{H_{3}O^{+}} (1)

Aktivita sa dá vyjadriť pomocou koncentrácie a aktivitného koeficientu, rovnica (2)

a_{H_{3}O^{+}} = \gamma_{\pm} c_{H_{3}O^{+}} (2)

kde \gamma_{\pm} je stredný aktivitný koeficient.

Aktivitný koeficient HCl dobre vyjadruje rovnica (3), ktorá vychádza z Debyeovej a Hückelovej teórie silných elektrolytov iónov sa dá vypočítať e podľa rovnice

- \log \gamma_{\pm} = \frac{0.508 \sqrt{I}}{1 + \sqrt{I}} - 0.1I (3)

kde I je iónová sila, ktorá je vyjadrená pomocou rovnice (4)

I = \frac{1}{2} \sum{c_{i}z_{i}^{2}} (4)

ci je koncentrácia príslušného iónov silného elektrolytu a zi je jeho náboj. Pre uni – uni valentný elektrolyt, ktorým je aj HCl platí že c=I.

Ak - \log a_{H_{3}O^{+}} = 1 potom zlogaritmovaním rovnice (2) dostaneme rovnicu (5)

I = - \log \gamma_{\pm} - \log c (5)

dosadením rovnice (3) do rovnice (5) dostaneme rovnicu (6)

I = - \frac{0.508 \sqrt{c}}{1 + \sqrt{c}} - 0.1c - \log 0.1c (6)

Takáto rovnica sa nedá riešiť analyticky. Takúto rovnicu môžeme riešiť iteračne alebo graficky

a) Iteračné riešeniee

V prvom priblížení budeme považovať aktivitný koeficient \gamma_{\pm} = 1 . V takomto prípade by mal roztok o koncentrácii c(l)HCl = 0.1 mol.dm-3 a I(l) = 1. Dosadením tejto hodnoty do rovnice (3) a vypočítame aktivitný koeficient v prvej iterácii

\gamma_{\pm (1)} = 10^{\big(\frac{0.508*\sqrt{0.1}}{1+\sqrt{0.1}} - 0.1*0.1 \big)} = 0.7726

Hodnotu \gamma_{\pm (1)} = 0.7726 použijeme v druhej iterácii. V tomto prípade bude na základe rovnice (2) c_{2} = \frac{a_{H_{3}O^{+}}}{\gamma_{H_{3}O^{+}}} = \frac{0.1}{0.7726} = 0.1294 mol.dm^{-3} a túto hodnotu opäť dosadíme za do rovnice (3)

\gamma_{\pm (2)} = 10^{\big(\frac{0.508*\sqrt{0.1294}}{1+\sqrt{0.1294}} - 0.1*0.1294 \big)} = 0.7560

Hodnotu \gamma_{\pm (2)} = 0.7560 použijeme v tretej iterácii. V tomto prípade bude koncentrácia c_{2} = \frac{a_{H_{3}O^{+}}}{\gamma_{H_{3}O^{+}}} = \frac{0.1}{0.7560} = 0.1323 mol.dm^{-3} a opäť ju použijeme na výpočet aktivitného koeficientu \gamma_{\pm (3)} = 10^{\big(\frac{0.508*\sqrt{0.1223}}{1+\sqrt{0.1223}} - 0.1*0.1223 \big)} = 0.7546

c_{(3)} = \frac{a_{H_{3}O^{+}}}{\gamma_{H_{3}O^{+}}} = \frac{0.1}{0.7546} = 0.1325 mol.dm^{-3}

Z rozdielu hodnôt koncentrácií HCl po druhej a tretej iterácii vyplýva, že ďalšia iterácia nemá význam. Vodný roztok HCl s koncentráciou 0.1325 mol.dm-3 má pH=1.

b) Grafické riešeniee

Úpravou rovnice (6) dostaneme funkciu f(c) (7) ktorú môžeme znázorniť graficky. Zvolíme si niekoľko koncentrácií HCl tak, aby funkcia f(c) nadobúdala kladné aj záporné hodnoty. Hľadaná koncentrácia HCl je tá, pri ktorej f(c) = 0. Táto závislosť je znázornená na obr. 3.

f(c) = \frac{0.508 \sqrt c}{1 + \sqrt c} - 0.1 c - \log c -1 (7)


c_{HCl}/mol.dm^{-3} f(c)
0.1 0.112049
0.11 0.074129
0.12 0.039519
0.13 0.00768
0.14 -0.02181
0.15 -0.04927

Tabuľka 1 Závislosť f(c) od koncentrácie HCl


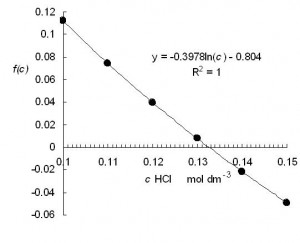
Obr. 1 Závislosť f(c) od koncentrácie HCl

Závislosť na obr. 1 bola vyhodnotená programom EXCEL. Z tejto závislosti vidno, že funkcia f(c) = 0 pri c=0.1325 mol.dm-3 čo je tá istá hodnota ako hodnota po tretej iterácii. Závislosť na obr. 1 sa dala dobre aproximovať rovnicou (8)

f(c) = -0.3978 \ln c_{HCl} - 0.804 (8)

z tejto rovnice môžeme tiež vypočítať koncentráciu HCl. Pre f(c) = 0 bude koncentrácia c_{HCl} = e^{- \frac{0.804}{0.3978}} = 0.1325 mol.dm^{-3} rovnaká hodnota ako v predchádzajúcich výpočtoch.

Napísať príspevok