The article deals with the use of fuzzy logic at support of manager decision making. The brief description of fuzzy logic and the process of calculation are mentioned. The usage is presented on the example, whether to solve or not the legal dispute by means of judicial process. The scheme of models, rule blocks, attributes and their membership functions are mentioned. The use of fuzzy logic is the advantage especially at decision making processes at law uncertainty.

1. Introduction

The use of fuzzy logic is the advantage especially at decision making processes where the description by algorithms is very difficult and criteria are multiplied. The advantage is that the linguistic variables are used. The fuzzy logic measures the certainty or uncertainty of membership of element of the set. Analogously the man makes decision during the mental and physical activities. The solution of certain case is found on the principle of rules that were defined by fuzzy logics for similar cases. The fuzzy logics belong among methods that are used in the area of decision making of firms and offices.

2. Fuzzy Logic

The calculation of fuzzy logics consists of three steps: fuzzification, fuzzy inference and defuzzification.

• The fuzzification means that the real variables are transferred on linguistic variables. The definition of linguistic variable goes out from basic linguistic variables, for example, at the variable profit is set up the following attributes: none, very low, low, medium, high, very high profit. Usually there are used from three to seven attributes of variable. The attributes are defined by the so called membership function, such as , , Z, S and some others. The membership function is set up for input and output variables.
• The fuzzy inference defines the behavior of system by means of rules of type <When>, <Then> on linguistic level. The conditional clauses evaluate the state of input variables by the rules. The conditional clauses are in the form

<When> Input_a <And> Input_b ….. Input_x <Or> Input_y …….. <Then> Output₁ , <With> x

it means, when (the state occurs) Input_a and Input_b, ….., Input_x or Input_y, …… , then (the situation is) Output₁ with x.

The fuzzy logic represents the expert systems. Each combination of attributes of variables, incoming into the system and occurring in condition <When>, <Then>, presents one rule. Every condition behind <When> has a corresponding result behind <Then>. It is necessary to determine every rule and its degree of supports (the weight of rule in the system). The rules are created by the expert himself.

• The defuzzification transfers the results of fuzzy inference on the output variables that describe the results verbally (for example, whether to accept or reject the client).

The system with fuzzy logics can work as an automatic system with entering input data. The input data can be represented by many variables.

3. Case Study

Let us mention an example, when it will be evaluated whether to solve or not the legal dispute by means of judicial process. Whether the judicial process reject (RJP), entertain the acceptance (EJP) or accept (AJP) on the basis of inputs. The input variables and their attributes are: Costs of disputes (low, medium, high), Time of duration of the dispute (low, medium, high), Success of the dispute (low, medium, high), possible Material Profit for the client (low, medium, high), possible Nonmaterial Profit for the client (low, medium, high). The task will be solved by means of MATLAB program using Fuzzy Logic Toolbox. It is suitable to set up an executable program to realize the mentioned task. The sequence of orders is as follows. See prog.1.

b2 = readfis('LD.fis');
Data = input('Set up the values in an order Costs; Time; Success; MProfit; NProfit; [Costs; Time; Success; MProfit; NProfit]: ');
result = evalfis(Data, b2);
fuzzy(b2)
mfedit(b2)
ruleedit(b2)
surfview(b2)
ruleview(b2)
result
if result<0.20 'Reject' elseif result<0.50 'Entertain' else 'Accept' end

Prog. 1 File LD.m

The first row reads the parameters of fuzzy model into variable b2 by order readfis from file LD.fis. The second row reads the five input variables such as Costs, Time, Success, MProfit, NProfit. The fourth row contains the order evalfis, that evaluates the input variables Data and b2. The output is in variable Result. The following order fuzzy(b2) enables the set up of fuzzy model, the order mfedit(b2) enables the set up of membership functions, the order ruleedit(b2) enables the set up fuzzy rules, the order surfview(b2) enables the graphical search of dependence of input and output variables and order ruleview(b2)enables to evaluate the output on the basis of inputs. The order result writes off the final value. The following four rows make a vague result. If the output value result is in the range R(0,20>, the result is to Reject the juridical process. If the output value result is in the range R(20,50>, the result is to Entertain the juridical process. 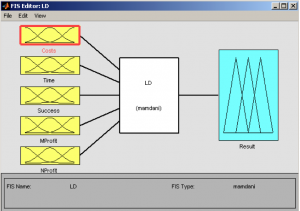If the output value result is in the range R(50,100), the result is to Accept the juridical process. The order fuzzy(b2) enables the set up of fuzzy model. See fig.1. The order mfedit(b2) enables the set up the membership functions of variables Costs, Time, Success, MProfit, NProfit and Result.

Fig. 1 Order mfedit(b2) – LD

The order mfedit(b2) enables the set up of membership functions. Fig.2 defines the attributes and membership functions for Costs of disputes - low (LC), medium (MC) and high (HC). Fig.3 defines the attributes and membership functions for Time of duration of the dispute - low (LT), medium (MT) and high (HT). Fig.4 defines the attributes and membership functions for Success of the dispute - low (LS), medium (MS), high (HS). Fig.5 defines the attributes and membership functions for possible Material Profit for the client - low (LM), medium (MM) high (HM). Fig.6 defines the attributes and membership functions for possible Nonmaterial Profit for the client - low (LN), medium (MN) and high (HN).

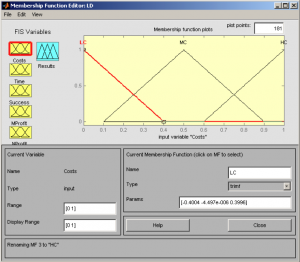
Fig. 2 Order mfedit(b2) – Costs

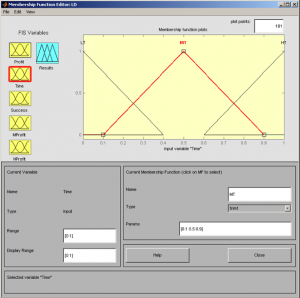
Fig. 3 Order mfedit(b2) – Time

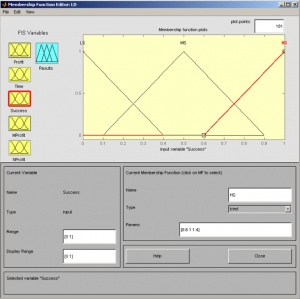
Fig. 4 Order mfedit(b2) – Success

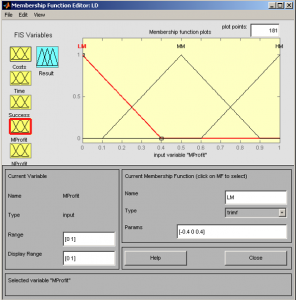
Fig. 5 Order mfedit(b2) – MProfit

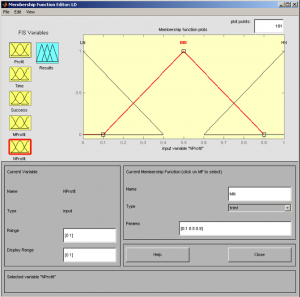
Fig. 6 Order mfedit(b2) – NProfit

Fig.7 defines the attributes and membership functions for Result Reject (RJP), Entertain (RJP) or Accept (RJP) the juridical process.

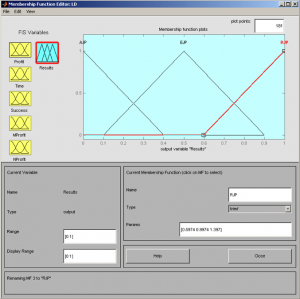
Fig. 7 Order mfedit(b2) – Result

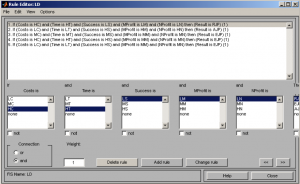
The way of set up of the first rule is on the fig.8 and its verbal interpretation is as follows: If the Costs is high (Costs = HC) and together the Time is high (Time = HT) and together Success is low (Success = LS) and together the value of Material profit for the client is low (MProfit = LM) and together the Nonmaterial profit for the client is low (NProfit = LN), then the result is the rejection of judicial process (Result = RJP) with weight 1.

The other rules are set up accordingly. The created rules are possible to check in the table of rules at upper part of display. It is necessary to set up such number of rules that describe the solved task.

Fig. 8 Order ruleedit(b2)

The order ruleview(b2) enables to evaluate output Result on the basis of inputs Costs, Time, Success, MProfit and NProfit. The following cases represent two set up rules. The ranges of variables are normalized in range <0,1>. Fig.9 presents the input variables with values Costs =1.0, Time = 1.0, Success = 0.0, MProfit = 0.0, MProfit = 0.0, that results in this case to value Result = 0.13, it means to Reject the juridical process. Fig.10 presents the input variables with values Costs =0.0, Time = 0.0, Success = 1.0, MProfit = 1.0, NProfit = 1.0, that results in this case to value Result = 0.87, it means to Accept the juridical process. The ranges and abbreviation of attributes of variables is as follows: Costs <0-1> <LC,MC,HC>; Time <0-1> <LT,MT,HT>; Success <0-1> <LS,MS,HS>; MProfit <0-1> <LM,MM,HM>; NProfit <0-1> <LN,MN, HN> and Result <0-1> <RJP,EJP,AJP>.

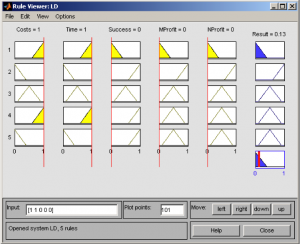
Fig. 9 Order ruleview(b2 ) – Input [1;1;0;0;0]

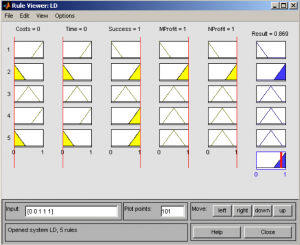
Fig. 10 Order ruleview(b2 ) - Input [0;0;1;1;1]

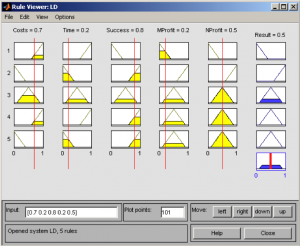
Fig. 11 Order ruleview(b2 ) - Input [0.7;0.2;0.8;0.2;0.5]

It is possible to use the model in practice, when the build up model is verified and its result corresponds to the reality. In this case the values of input variables are set up on the basis of real client. The set up is done by movement of vertical lines. See fig.11 for values Costs =0.7, Time = 0.2, Success = 0.8, MProfit = 0.2 and NProfit = 0.5.

When the program LD.m is started, the request for entering the input data is displayed in the form Costs, Time, Success, MProfit, NProfit. When the input values are written [1;1;0;0;0], the result is to Reject the juridical process. When the input values are written [0;0;0;1;1], the result is to Accept the judicial process. When the input values are written [0.7; 0.2; 0.8; 0.2; 0.5] the result is to Entertain the juridical process. See fig.12.

Set up the values in an order Costs; Time; Success; MProfit; NProfit; [Costs; Time; Success; MProfit; NProfit]: [1;1;0;0;0]
ans = Reject
Set up the values in an order Costs; Time; Success; MProfit; NProfit; [Costs; Time; Success; MProfit; NProfit]: [0;0;1;1;1]
ans = Accept
Set up the values in an order Costs; Time; Success; MProfit; NProfit; [Costs; Time; Success; MProfit; NProfit]: [0.7;0.2;0.8;0.2;0.5]
ans = Entertain

Fig. 12 Result of the legal dispute

The results correspond to reality therefore it is possible to consider the build up model to be functional. All graph generated by orders fuzzy(b), mfedit(b), ruleedit(b), surfview(b) and ruleview(b) are at disposal after calculation. The parameters of the build up model are saved in a LD.fis file.

5. Conclusion

The fuzzy logic is used for the decision making process whether the legal disputes will be accepted, entertained or rejected. The use of fuzzy logic is suitable in the cases when vague notes are used. The low profession belongs among these cases.

Literature

1. Aliev, A.; Aliev, R. Soft Computing and Its Applications. World Scientific Publishing Ltd, UK2002, 444s., ISBN 981-02-4700-1.
2. DOSTÁL, P. Pokročilé metody analýz a modelování v podnikatelství a veřejné správě. Brno: CERM, s.r.o., 2008. 340s. ISBN 978-80-7204-605-8.
3. DOSTÁL, P.; RAIS, K.; SOJKA, Z. Pokročilé metody manažerského rozhodování. Praha: Grada, 2005.168s. ISBN 80-247-1338-1.
4. DOSTÁL, P. Pokročilé metody rozhodování za právní nejistoty, Brno: CERM, s.r.o., 2009,104s. ISBN 978-80-7204-651-5.
5. DOSTÁL, P., Orgoník, M. Využití fuzzy logiky pro rozhodování o formě řešení obchodně-právní sporů, In Spisy Právnické fakulty Masarykovy univerzity, Brno, 2009, s44., 8s, ISBN978-80-210-4989-5.
6. DOSTÁL, P. Využití programových prostředků MATLAB pro rozhodování za právní nejistoty, Praha, In Technical Computing Prague, 2009, Konference, s23., 6s, ISBN 978-80-7080-733-0.
7. Klir,G.J., Yuan, B. Fuzzy Sets and Fuzzy Logic, Theory and Applications, Prentice Hall, New Jersy, USA, 1995, ISBN 0-13-101171-5.
8. THE MathWorks. MATLAB – Fuzzy Logic Toolbox - User’s Guide, The MathWorks, Inc., 2008.

---

Address:Faculty of Business and Management, Department of Informatics, Kolejní 4, 612 00 Brno