In solving many practical search/optimization problems using evolutionary algorithms it is often difficult to avoid the premature convergence in search for the global optimum. From that reason parallel evolutionary algorithms (PEA) and Parallel Genetic Algorithms (PGA) with advantage can be used. In this paper some selected fine- and coarse-grained PGA architectures are analysed and experimentally compared. Also the influence of population re-initialization on the parallel genetic algorithm performance is analysed. The results are demonstrated on the minimization of selected test functions.

Parallel evolutionary algorithms are able to improve the performance of simple evolutionary algorithms with a single population. From some point of view they can be divided into two groups: fine-grained and coarse-grained architectures. This paper is an extension of a previous project (Sekaj and Perkacz, 2007), where only some types of coarse-grained PGA’s and their re-initialization have been analysed.

Similarly as in the living nature, evolution is not a time-synchronous process from the geographical point of view. The evolution is distributed into many more or less isolated groups (subpopulations) and individuals, where the transfer of genetic information among these groups has an important influence on the evolution process. If the information transfer is too rare, there is a higher variability among the individual subpopulations. On the other hand, if the information transfer between subpopulations is more frequent or more “dense”, properties of representatives of all subpopulations are more similar. From some time-point the evolution starts stagnating due to insufficient gene diversity. A new radical qualitative improvement or even change to new quality can be brought about only by dramatically environmental changes or some natural disasters. The same principles are valid also in the parallel genetic algorithms.

There are several important factors, which have influence on the behaviour and performance of the PGA, e.g.: migration structure between subpopulations (architecture of migration interconnections), size of subpopulations and other possible factors. Several authors have studied various factors and their influence on the behaviour of PGA`s or EA`s. Surveys and island model behaviour analyses are in (Cantú-Paz, 1995; Chipperfield and Fleming, 1994; Whitley, et al., 1999), etc. Migrations have been studied in (Cantú-Paz, 2001). The impacts of migration size and migration intervals were experimentally analysed in (Skolicki and De Jong, 2005). Various PGA architectures, the influence of heterogeneity of subpopulations and some re-initialization possibilities are analysed in (Sekaj, 2004).

An important GA and PGA characteristic having influence on the convergence properties is the population diversity, which is a measure of gene variance. With its increase it is possible to escape the algorithm from the current local optimum and redirect it to better solutions, possibly to the global optimum. Factors that increase population diversity are the operators modifying the current individuals in the population e.g. mutation (mutation rate). However, if using mutation in case of highly non-smooth search/optimization problems like (technical design/optimization problems) it is sometimes not possible to avoid the premature convergence. An effective means to increase the population diversity (an analogy to natural disasters in the living nature) is the population re-initialization.

This paper deals with an experimental comparison of some representatives of fine/coarse – grained PGA’s and the influence of population re-initialization on their performance.

Parallel GA architectures

In our comparison 2 coarse-grained, 4 fine-grained PGA’s and a simple GA are analysed and experimentally compared. The coarse-grained PGA (C-PGA) type consists of 9 subpopulations (nodes), which are interconnected with other nodes through defined migration connections (Fig.1). The migrations are performed by replacing a randomly selected individual (except of the best one) in the target node by a copy of the best individual from the source node (best-random policy). The number of individuals in each node is set to 60. The number of all individuals in the entire PGA is 9×60=540. The migration in the C-PGA according to the defined connections is realized periodically after 100 generations.

The fine-grained PGA (F-PGA) has the architecture, which is depicted in Fig.2. In this case each node represents a single individual. There are 540 individuals, which are located in a 2D grid with 27 rows and 20 columns. Each individual in each generation is crossed-over with another neighbour, which is selected from all 8 possible neighbour candidates using stochastic universal sampling selection. The crossover rate is 0.95. From the two new children a randomly selected one replaces the parent. Next the mutation, with the mutation rate 0.002 is performed, where the mutated gene is randomly selected (with uniform distribution) from its entire search space (global mutation). Additionally another mutation is performed (mutation rate 0.002) where the new mutated gene is selected randomly from a small area around the parent gene (local mutation). The used size of the area has been set to 2% of the search space size.

In both PGA cases a re-initialization of the population has been performed. In the C-PGA two types of re-initialization have been used:

• R_c1 – the simple case is the periodical re-initialization of all individuals in the specified nodes. This means that in all nodes of the PGA, expect the node 1, in defined computation periods (after each 100 generations) all individuals are replaced by new randomly generated ones. Note, that before the re-initialization the best individual from the entire PGA is inserted into the population of the node 1
• R_c2 – in the second method the re-initialization is activated in each node independently. The condition for the re-initialization is that a defined number of individuals in this node are identical, i.e. that for each of the N individuals in the node there exists at least one other individual, which Euclidean (or absolute) distance is less than a very small number . In our experiments N was set to 1/3 of the population size and was set to 0.01 % of the search space.

In the F-PGA case only one re-initialization type has been considered – R_f, where in each generation 100 randomly selected individuals are re-initialized (expect the best individual). The number 100 was set experimentally.

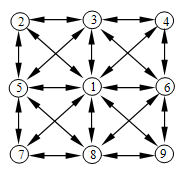
Fig.1 Considered coarse-grained PGA architecture

Fig.2 Considered fine-grained PGA architecture

The genetic algorithm, which is used in each node of the C-PGA and in the SGA is as follows:

1. Population initialization (random) and fitness calculation.
2. Selection of 2 best individuals, which are without any change copied into the new population – Pop1. Random selection of a group of 6 individuals, which are copied without any change into the new population – Pop2. Selection (tournament) of 12 parents – Pop3.
3. Mutation and crossover of parents – Pop3’.
4. Completion of the new population by unification of the groups Pop1, Pop2 and Pop3’.
5. New population fitness calculation.
6. 1.Test of terminating condition, if not fulfilled, then jump to the Step 2.

As in the F-PGA two contemporary mutation types have been used. In the global mutation the mutated gene has been replaced by a random (real) value from the entire search space with uniform probability distribution. In the local mutation there are small random real numbers added to (or subtracted from) the original gene values. The used size of random additive changes was limited to 2 % of the entire search space, with a uniform distribution and a zero mean value. The mutation rate for both mutation types was 0.05. In case of crossover a simple one-point crossover has been used.

Experiment description and results

In our analysis 7 PGA architectures are considered. In each case the entire population size is 540 individuals (in all subpopulations of the C-PGA and in the F-PGA). All PGA types are compared with a single-node GA (SGA). The number of individuals in the SGA is also 540. The C-PGA uses the migration architecture according Fig.1. The first considered type do not use re-initialization (in the experiments it is marked C0), next the version with re-initialization Rc1 (C1) and Rc2 (C2) respectively are considered. The F-PGA’s have the architecture according Fig.2. The first type is without re-initialization (F0). The second type is using re-initialization Rf (F1). The third F-PGA type is creating a group of individuals consisting of new offspring (after mutation and crossover) and the current population of size N individuals. From all these a new population of N individuals is selected applying tournament selection. This algorithm type combines features of the fine-grained PGA with Rf re-initialization with a single population GA (F2). The last F-PGA case represents a parallel run of F-PGA (with 520 individuals, Rf re-initialization) with a single population GA with population size of 20 individuals. In each generation the copy of the current best individual from the F-PGA is placed into the single population GA (F3).

The following test functions have been used in the analysis:

f₁(x) – “Schwefel function”

(1)

The global minimum is in f(x)=-n.418.9829; x_i=420.9687. In our case n=10. Graph of f₁(x1, x2) for the two variable case is in Fig. 3.

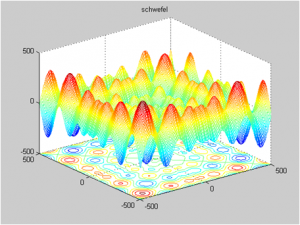
Fig.3 f1(x) – Schwefel function

f₂(x) – “Three Holes function”

function with 3 variables, which is a sum of a quadratic function, the Schwefel function and 3 Gauss peaks (holes). if i=1,2,3

(2)

otherwise

(3)

The global minimum is f₂(x₁,x₂,x₃)=–1000; x₁=x₂=x₃=0. This function belongs to the category of “deceptive functions”, for which the search for the global optimum is not an easy problem, because of “unexpected” position of the global optimum. Graph of f₂(x1, x2) for the two variable case is in Fig. 4.

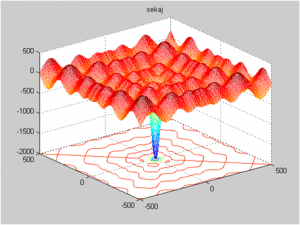
Fig.4 f₂(x) – Three Holes function

f₃(x) – “Egg holder function”

(4)

where X={x₁,x₂,…,x₁₅}. In our case n=15. Graph of f₃(x1, x2) for the two variable case is in Fig. 5.

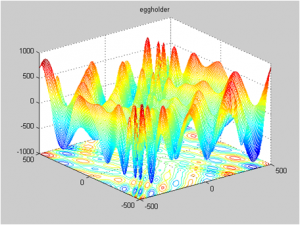
Fig.5 f₃(x) – Egg holder function

f₄(x) – “Langermann function”

(5)

where c_i and A_i are vector resp. matrix of constants . In our case m=5 and the global minimum is f(x)=-1.4. Graph of f₄(x1, x2) for the two variable case is in Fig. 6.

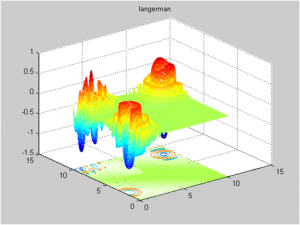
Fig.6 f₄(x) – Langermann function

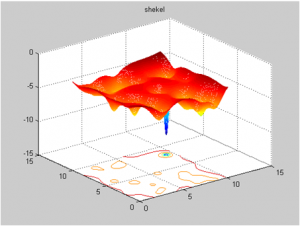
f₅(x) – “Shekel function”

(6)

where c_i and A_i are vector resp. matrix of constants . The global minimum for n=5 (our case) is in f(x)=-10.4056. Graph of f₅(x1, x2) for the two variable case is in Fig. 7.

Fig.7 f₅(x) – Shekel function

The aim of the experiments was to compare the performance of the mentioned PGA architectures. The performance has been measured in a standard way using the convergence rate of the fitness function, which is the graph of the test function values of the currently best individual in the entire PGA (“best so far” from all subpopulations). In all graphs this value is labelled as “F(x)”. In our case the F(x) is to be minimized. Each graph represents the mean value of 30 PGA runs.

In figures 8 to 12 all PGA types (C0, C1, C2, F0, F1, F2, F3) and the SGA are compared on minimization of functions f₁ to f₅. The convergence rate of Schwefel function (f₁) minimization is similar for all PGA types expect F2 and F0. F2 is the most successful type for this relative simple problem. For F0 the convergence rate is very slow. Expect the f1 all other test cases are non-smooth functions. Here in general the algorithm types with re-initialization (C1, C2, F1, F2, F3) are more successful, than types without re-initialization (C0, F0, SGA). This is evident in case of the highly non-smooth Three Holes function. The performance of the type F2 is slower, than of other types, which is probably caused by a higher selective pressure of this algorithm in comparison with other (expect SGA). The most successful types are F3, C1 and C2. C1 and C2 have a high measure of gene diversity of the population, thank relatively isolated subpopulations and the use of re-initialization. In the C-PGA the more powerful re-initialization method is the R_c2 method. The most powerful PGA type for test functions f₁ to f₅ is the F3 type, which is a combination of a fine-grained PGA with re-initialization and a simple GA with a small population with 20 individuals. In the F-PGA there is a sufficient diversity measure for new search directions generating and the simple GA “finalize the evolution” and finds the best solution

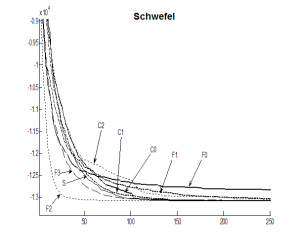
Fig. 8 Comparison for test function f₁

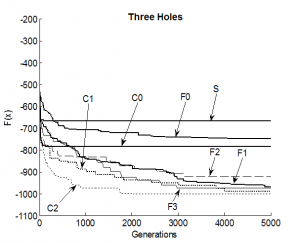
Fig. 9 Comparison for test function f₂

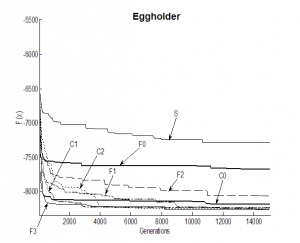
Fig. 10 Comparison for test function f₃

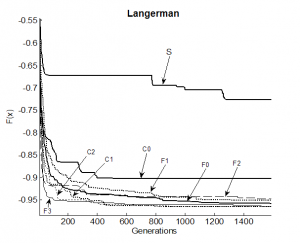
Fig. 11 Comparison for test function f₄

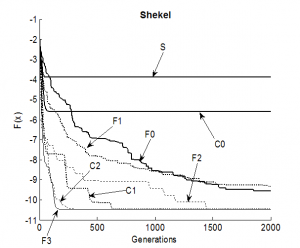
Fig. 12 Comparison for test function f₅

Conclusion

Conclusion from experiments obtained by minimizing the test functions f₁ to f₅, but also other non-smooth multi-modal functions and some complex practical optimization problems are as follows. The PGA or even parallel evolutionary algorithms can increase the gene diversity in the population. An effective means of diversity increase is also the population re-initialization. This can increase the convergence rate of the PGA and avoid the premature convergence.

Selection of various coarse-grained or fine-grained PGA architecture types has some influence on the convergence rate. The fine-grained PGA type F3 and coarse-grained PGA type C2 seems to give the best performance. PGA’s can bring decrease of computation time, which is needed to find good (or even the best) solution of complex problems thanks their architecture and information exchange between subpopulations or individuals respectively.

References

1. T. Bäck (1994), “Selective pressure in evolutionary algorithms: A characterization of selection mechanisms”, in ICEC-94, pp. 57-62.
2. E. Cantú-Paz (1995), “A summary of research on parallel genetic algorithms”, IlliGAL Report No. 95007, Illinois Genetic Algorithms Laboratory, University of Illinois at Urbana Champaign.
3. E. Cantú-Paz (2001), “Migration polices, selection pressure, and parallel evolutionary algorithms”, in Journal of heuristics 7(4), pp. 311-334.
4. A. J. Chipperfield, P. J. Fleming (1994), “Parallel genetic algorithms: A survey”, ACSE Research Report No.518, University of Sheffield.
5. Z. Michalewicz (1996), “Genetic Algorithms + Data Structures = Evolution Programs”, 3rd ed. Springer-Verlag, Berlin Heidelberg New York.
6. I. Sekaj (2004), “Robust Parallel Genetic Algorithms with Re-Initialization”, in PPSN VIII, September 18-22, Birmingham.
7. I.Sekaj and J.Perkacz (2007), “Some Aspects of Parallel Genetic Algorithms with Population Re-initialization”, In Proceedings on CEC’07, Singapore
8. Z. Skolicki, K. De Jong (2005), “The influence of migration sizes and intervals on island models”, in GECCO`05, June 25-29, Washington DC, USA.
9. D. Whitley (1989), “The GENITOR Algorithm and Selection Pressure: Why Rank-based Allocation of Reproductive Trials is Best”, in Proceedings of the Conf. of Genetic Algorithms, Morgan Kaufmann Publ., San Mateo, CA, pp.116-121.
10. D. Whitley, S. Rana, R. B. Heckendorn (1999), “The island model genetic algorithm: On separability, population size and convergence”, in Journal of Computing and Information Technology, 7(1), pp.33-47.

---

Co-author of this paper is doc. Ing. I. Sekaj PhD., Slovak University of Technology, Faculty of Electrical Engineering and Information Technology, Ilkovičova 3, 812 19 Bratislava.