Fuzzy logic autotuning methods for predictive controller
12. Júl, 2010, Autor článku: Paulusová Jana, Elektrotechnika
Ročník 3, číslo 7  Pridať príspevok
Pridať príspevok

In this paper a new method for predictive auto-tuning PID fuzzy logic controller (predictive FPID) is proposed, analyzed and tested. The paper contains theoretical as well as practical part and offers a new approach to control design and its successful application. The proposed predictive controller is used to control nonlinear process. The results show that the proposed algorithm is capable of an effective control.
1 Introduction
The PID algorithm is both simple and reliable, and has been applied to thousands of control loops in various industrial applications over the past 60 years (89%-90% of applications). However, not all industrial processes can be controlled using conventional PID algorithms.
Concept of the model based predictive control (MBPC) has been heralded as one of the most significant control developments in recent ten years. The wide range of choice of model structures, prediction horizon, and optimization criteria allows the designer to easily tailor MBPC to his application in industry.
In this paper method for auto-tuning of a SISO predictive controller is proposed and advanced for nonlinear process.
The paper is organized as follows. First, auto-tuning of fuzzy PID controller (FPID) is described in Section 2. Design of predictive FPID is presented in Section 3. The reliability and effectiveness of the presented method is shown on the case study in Section 4 – control of the concentration in chemical reactor by manipulating its inlet flow rate. Summary and conclusions are given in Section 5.
2 Autotunning of Fuzzy PID Controller
Since the proposed controller uses nonlinear fuzzification algorithm and output membership functions, the controller can be considered as a nonlinear PID where parameters are tuned on-line based on error e(t) and change of error compared to set-point
(Almeida, et al, 2002).
The system error is compensated by a set of fuzzy linguistic rules which are derived from the experience and knowledge of a control designer on how the behavior of gain and phase margins can be used to compensate the system error efficiently. It can be interpreted as a fuzzy gain scheduling PID controller. Fuzzy logic controller system for nonlinear process is shown in Figure 1, where is control output.
Firstly, identification of a process model and design of a conventional PID is necessary to be done as a starting point. After that, the fuzzy engine is designed.
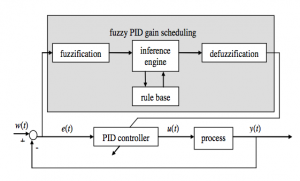
Figure 1 Fuzzy logic controller (FPID) system for SISO system
2.1 Identification of process and initial PID parameters
An approximated model for the process is considered as a second order transfer function with time delay, which is given by
| (1) |
Where and
are unknown parameters and they need to be determined by a feedback relay experiment. Depending on
the model may have real or complex poles and it is representing both monotonic and oscillatory processes. Under relay experiments, the parameters are given by
| (2) |
| (3) |
Where yr(t) is process output and ur(t) is relay output. Ku is process critical gain and ωu is frequency. The initial PID parameters are determined considering the following transfer function
| (4) |
Where A=Kd/k, B=Kc/k, C=Ki/k. The PID gains are Kc, Ki, Kd. Zeros of the controller are chosen to cancel the poles of the process model, A=a2, B=a1, C=a0.
| (5) |
Where k is obtained by considering the gain Am and phase margin Φm. The following relation can be derived
| (6) |
A typical value is Am=3 and Φm=60 ̊. The PID parameters are
| (7) |
2.2 Auto-tuning fuzzy logic controller engine
The gain and phase margins are considered to be linguistic variables whose values are defined with respect to the same universe of discourse specified by human expertise about the operational knowledge of the process. It is assumed that the feedback system gain and phase margins are in prescribed ranges. Values of Am and Φm are normalized
| (8) |
| (9) |
where A’m and Φ’m are normalized gain and phase margins, respectively. Values of A’m are determined by a set of fuzzy rules of the form
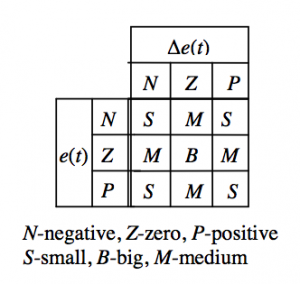
| If e(t) is Ai and ∆e(t) is Bi then A’m,i is Ci | (10) |
where i=1,…,n, Am,i is the gain margin for i-rule and Ai, Bi, Ci are fuzzy sets on the corresponding supporting sets.
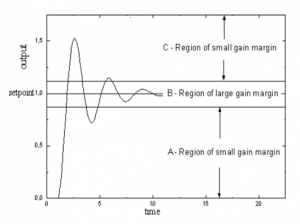
Figure 2 Process response and regions of gain margin
Figure 2 shows an example of a desired time response of the process. The membership functions are shown in Figure 3.
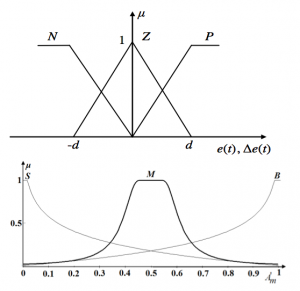
Figure 3 Membership functions for input and output variables
Where the fuzzy set Ci may be S-small, M-medium, B-big and it is characterized by logarithmic membership functions (11-13). The degree of the membership μ and the variable A’m are (Almeida, et al, 2002)
| (11) |
| (12) |
| (13) |
The adjustable parameters are η and δ. Based on μi, values of Am‘ for each rule are determined from their correspondent membership function. This theory for linear model has been extended for the nonlinear process. For control it is very important to set Am,min and Am,max. These values have effect on the quality of control.
3 Predictive control
The proposed predictive fuzzy control system is shown in Figure 4 (Paulusová, et al. 2006). It is composed of a fuzzy model (ANFIS) and FPID. In Figure 4, w(t) is the reference variable y(t) is nonlinear plant output, u(t) is control input of the plant, u(t) is output of the controller and ŷ(t) is predicted value of y based on the predictive fuzzy model. To achieve the objective of predictive control, the fuzzy model has been used as a predictor to predict ŷ(t).
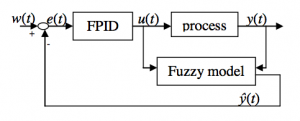
Figure 4 Proposed predictive fuzzy control system
4 Case study and simulation results
4.1 Case study
The application considered involves an isothermal reactor in which the Van Vusse reaction kinetic scheme is carried out. In the following analysis, A is the educt, B the desired product, C and D are unwanted byproducts.
| (14) |
From a design perspective the objective is to make k2 and k3 small in comparison to k1 by appropriate choice of catalyst and reaction conditions. The concentration of B in the product may be controlled by the manipulating the inlet flow rate and/or the reaction temperature.
The educt flow contains only cyclopentadiene in low concentration, CAf. Assuming constant density and an ideal residence time distribution within the reactor, the mass balance equations for the relevant concentrations of cyclopentadiene and of the desired product cyclopentanol, CA and CB, are as follows:
| (15) |
This example has been considered by a number of researchers as a benchmark problem for evaluating nonlinear process control algorithm. By normalizing the process variables around the following operating point and substituting the values for the physical constants, the process model becomes:
| (16) |
where the deviation variable for the concentration of component A is denoted by x1, the concentration of component B by x2, and the inlet flow rate by u. The simulation scheme of this process is in Figure 5 (Paulusová, et al. 2007).
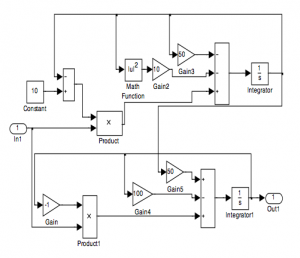
Figure 5 Simulation scheme for the nonlinear process described by (16)
4.2 Fuzzy model
Fuzzy model was created in ANFIS editor (in MATLAB). The model has two inputs and each of them has five triangular membership functions. Number of rules is 25. The comparison of process and its fuzzy model is shown in Figure 6.
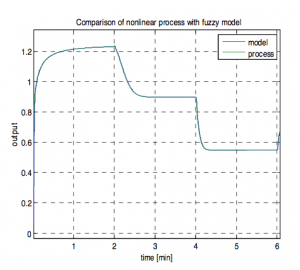
Figure 6 Comparison of fuzzy model and nonlinear process
4.3 Predictive control
Fuzzy controller is designed for a nonlinear process given by (16). The fuzzy controller has three membership functions.
The membership functions for input (e, ∆e) and output ( Am‘ ) variables are shown in Figure 4. The rule base of the fuzzy controller is shown in Table 1. The fuzzy controller is designed with nine rules.
The relay feedback experiment is used to tune PID parameters around an operational point. The time responses of the controlled and reference variables of the nonlinear process controlled by predictive FPID (Figure 4) is shown in Figure 7.
The performance of the control by predictive FPID is also depended on a suitable choice of Am. Detailed procedure of Am choice is part of future work.
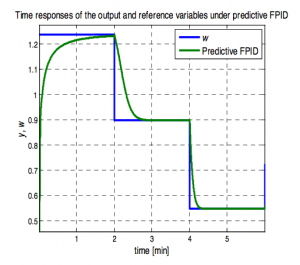
Figure 7 Time responses of the controlled and reference variables of the nonlinear process under predictive FPID with Am∈<0.747;2.253>
Conclusions
In this paper a fuzzy logic auto-tuning methods for predictive PID controller parameters have been applied to the concentration control in the chemical reactor by manipulating its flow rate. The performance of predictive FPID controller is dependant on a suitable choice of Am parameter.
Acknowledgement
This paper has been supported by the Slovak Scientific Grant Agency, Grant No. 1/0544/09.
References
- ALMEIDA, O.M.; COELHO, A.A.R. 2002. A fuzzy logic method for autotuning a PID controller: SISO and MIMO systems. In.: 2002 IFAC 15th Triennial World Congress, Barcelona, Spain, 3031.
- P AULUSOVÁ, J.; KOZÁK, Š. 2006. Robust Predictive Fuzzy Control. In.: 7th Portuguese Conference on Automatic Control, CONTROLO’ 2006, Lisbon, Portugal: 11-13 September 2006, MA-7-1. ISBN.
- PAULUSOVÁ, J.; KOZÁK, Š.; DÚBRAVSKÁ, M. 2007. Fuzzy logic autotuning methods for PID controller applied to nonlinear process. In.: 16th International Conference on Process Control 2007, Process Control ’ 07, Štrbské pleso, Slovakia: 11-14 June 2007, 177s.pdf. ISBN.
Coauthor of this paper is M. Dúbravska, Institute of Control and Industrial Informatics, Faculty of Electrical Engineering and Information Technology, Slovak University of Technology, Ilkovičova 3, 812 19 Bratislava, Slovak Republic