Příspěvek se zabývá modelováním pohybu vozidel v síti linek MHD a navrhováním logiky řízení světelných křižovatek pomocí Petriho sítí. V úvodu je uveden význam problému tvorby sítě linek MHD, rozvoje individuální automobilové dopravy a motivace využití nástroje Petriho sítí. Následuje teoretická analýza včetně základní koncepce a rozdělení Petriho sítí. Pomocí P/T Petriho sítí je nastíněno řešení konkrétních příkladů.

1. Úvod

Městská hromadná doprava zaujímá v dopravní soustavě každého státu nezastupitelnou funkci z hlediska každodenní mobility obyvatelstva. Při jejím plánování je žádoucí zabývat se kromě tvorby tras linek také modelováním pohybu vozidel v navržené síti, což může souviset s hledáním optimální varianty provozu. V rámci procesu optimalizace MHD v tuzemsku i zahraničí existují matematické modely na tvorbu systémů linek MHD, které využívají pokročilé metody operačního výzkumu. K rozhodnutí, které linky vybrat tak, aby byla pokryta poptávka cestujících a určit jaký počet vozidel je třeba přiradit linkám, je využívána např. metoda PRIVOL (Přiřazení Vozidel Linkám), která patří mezi úlohy lineárního programování [1], [2].

S rozvojem mobility souvisí také zvyšující se zájmem o možnosti svobodné individuální volby. Zvyšující se zájem o individuální automobilovou dopravu ve 20. století představuje vzrůstající počty vozidel na jednoho obyvatele, což však na přetížených komunikacích a křižovatkách přináší zpomalování, resp. zastavování vozidel vedoucího ke vzniku kongescí, které jsou příčinou enormního a nadbytečného znečišťování ovzduší a souvisejících negativních vlivů. Z hlediska vzniku kongescí jsou nejkritičtějšími místy ve městech křižovatky a jejich okolí, situace může být kritická především u neřízených křižovatek. Za účelem odstraňování uvedených problémů na křižovatkách se vypracovávají návrhy úprav ve více variantách s dopravně ekonomickým posouzením vzhledem k životnosti řešení. Na základě dopravního a ekonomického posouzení je nutné vyhledat z dlouhodobého hlediska co nejpříznivější řešení.

2. Motivace

Petriho sítě představují významný formalismus pro modelování diskrétních systémů, který spojuje výhody srozumitelného grafického zápisu a možnosti simulace s dobrou formální analyzovatelností. Srozumitelnost a analyzovatelnost Petriho sítí je dána jejich jednoduchostí. Model je popsán místy (places), která obsahují stavovou informaci ve formě značek (tokens), přechody (transitions), které vyjadřují možné změny stavu a hranami (arcs), propojujícími místa a přechody navzájem. Existuje celá řada typů Petriho sítí a jejich speciálních podtřídy, až po vysokoúrovňové (High-Level Petri nets) a barevné sítě [3].

Existence různých variant Petriho sítí souvisí se snahou zvyšovat modelovací schopnosti a úroveň popisu modelu (přiblížit příslušný formalismus modelovaným skutečnostem) a přitom zachovat konceptuální jednoduchost, která je pro Petriho sítě příznačná. Obecně platí, že vyšší typy Petriho sítí jsou poněkud hůře analyzovatelné, poskytují však vyšší komfort při modelování.

Uplatnění Petriho sítí je značně široké, v oblasti dopravy však používání Petriho sítě doposud jako modelovacího, resp. optimalizačního nástroje příliš nerozšířilo. Smyslem je tedy zkoumat, zda Petriho sítě nemohou určitým způsobem přispět k řešení některých optimalizačních problémů v dopravě, případně odstranit některé nevýhody v současnosti používaných řešících nástrojů. V předloženém článku bude pomocí Petriho sítě prezentován pohyb vozidel v linkové síti MHD (obecně však jakékoliv síti linek) a návrh logiky řízení světelných křižovatek.

3. Základní koncept Petriho sítě

Jak je uvedeno např. v [3], využívají Petriho sítě ke své výstavbě následující koncept:

Parciální stavy systému jsou modelovány místy a možné jevy, které jsou aktivátorem změny, jsou definovány přechody. Okamžitý stav systému je definován umístěním značek (tokens) v místech, což se v grafu Petriho sítě vyjadřuje tečkami v místech. Přítomnost tokenu v místě modeluje skutečnost, že daný stav je momentálně aktuální. Každý přechod má definována vstupní a výstupní místa, což je v grafu Petriho sítě vyjádřeno orientovanými hranami mezi místy a přechody. Tím je dáno, které aspekty stavu systému podmiňují výskyt odpovídající události (provedení přechodu), a které aspekty stavu jsou výskytem této události ovlivněny.

Pro každý přechod jsou definovány vstupní a výstupní podmínky. Přechod může být proveden pouze v případě, že všechna jeho vstupní místa obsahují značky, tj. má splněny všechny vstupní podmínky. Provedením přechodu se odstraní značky ze vstupních míst (vstupní podmínky přestanou platit) a umístí se nové značky do výstupních míst (uplatní se výstupní podmínky). Provedení přechodu je atomická operace, která odpovídá výskytu události.

K modelování provozu bude v předloženém článku využito P/T Petriho sítí, které patří k základním Petriho sítím.

P/T Petriho síť je tvořena následujícími objekty:

• místy (places), graficky reprezentovanými kružnicemi,
• přechody (transitions), graficky reprezentovanými obdélníky, orientovanými hranami (arcs), graficky reprezentovanými šipkami směřujícími od míst k přechodům nebo od přechodů k místům,
• udáním kapacity (capacity indications) pro každé místo sítě, tj. přirozeného čísla udávajícího maximální počet tokenů, který se může v místě nacházet,
• udáním váhy (weights) pro každou hranu sítě, tj. přirozeného čísla udávajícího násobnost hrany,
• udáním počátečního značení (initial marking), udávajícího počet tokenů pro každé místo sítě.

Změny stavů (značení) P/T Petriho sítě jsou charakterizovány následujícími pravidly:

• stav sítě je určen značením, tj. počtem tokenů v každém místě,
• místo p patří do vstupní množiny (pre-set) přechodu t, jestliže z místa p vede hrana do přechodu t a místo p patří do výstupní množiny (post-set) přechodu t, jestliže z přechodu t vede hrana do místa p,
• přechod t je proveditelný (enabled, activated), jestliže:
  • pro každé místo p vstupní množiny přechodu t platí, že obsahuje alespoň tolik tokenů, kolik činí násobnost hrany vedoucí z místa p do přechodu t,
  • pro každé místo p výstupní množiny přechodu t platí, že počet tokenů obsažených v místě p zvětšený o násobnost hrany, mířící z přechodu t do místa p, nepřevyšuje kapacitu místa p,
• při provedení (firing) proveditelného přechodu t se změní stav (značení, marking) sítě takto:
  • počet tokenů v každém vstupním místě p přechodu t se zmenší o násobnost hrany spojující toto místo s tímto přechodem
  • počet tokenů v každém výstupním místě p přechodu t se zvětší o násobnost hrany spojující toto místo s tímto přechodem

Vstupní a výstupní podmínky přechodů specifikují počty odebíraných/umísťovaných značek. V grafu Petriho sítě se to vyjádří ohodnocením orientovaných hran do/z přechodu. Příklad změny stavu je znázorněn na obr. č. 1.

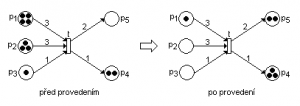
Obr. č. 1: Příklad změny stavu po provedení přechodu v P/T Petriho síti

V P/T Petriho sítích podle obvyklých zásad místa označují stavy modelovaného systému a přechody změny stavu. Stav je charakterizován celým nezáporným číslem daným značením daného místa (počtem tokenů v daném místě). Při modelování počítačových dějů, jedná se např. o počty jednotek volné nebo obsazené paměti (např. bufferu), o počty jednotek disponibilních nebo využívaných zdrojů různého typu apod.

Implicitně předpokládáme násobnost hrany 1 a kapacitu místa nekonečnou. Násobnost jednoduchých hran (w=1) a kapacitu kapacitně neomezených míst (K=nekonečno) na grafech Petriho sítí není nutné uvádět, především kvůli větší přehlednosti. Speciálním případem P/T Petriho sítí jsou C/E Petriho sítě, což jsou P/T Petriho sítě ve kterých je kapacita každého místa a násobnost každé hrany rovna 1.

4. Petriho sítě vyšší úrovně

Základní typy Petriho sítí byly postupně obohacovány a zobecňovány tak, aby schopnost tohoto modelovacího nástroje vyhověla praktickým potřebám. Dalšími typy Petriho sítí vzniklými rozšířením P/T sítí jsou:

• Petriho sítě s inhibičními hranami (P/T PN with inhibitors),
• Petriho sítě s prioritami (P/T PN with priorities),
• Časované Petriho sítě (Timed PN),
• Barevné Petriho sítě (Coloured PN),
• Hierarchické Petriho sítě (Hierarchical PN),
• Objektové Petriho sítě (Object-Oriented PN).

5. Specializovaný software pro sestavení Petriho sítě

Při vytváření Petriho sítě a následnou simulaci je nutné využít specializovaný software. V následující části budou popsány specializované software Snoopy a Pipe2, protože byly použity k řešení uvedených problematik s využitím Petriho sítí.

5.1 Software Snoopy

Při spuštění software se zadává v nabídce Templates (šablony) typ Petriho sítě, se kterou bude dále pracováno. Po zadání typu Petriho sítě se kromě základní obrazovky umožňující práci se souborem zobrazí také obrazovka umožňující sestavení Petriho sítě prostřednictvím přehledného menu a pracovní plochy. Výběrem příslušné položky z menu se sestavují jednotlivé prvky Petriho sítě na pracovní plochu, přičemž u každého místa je možné definovat Name (název), Marking (značení), Comment (komentář) a Graphic (grafickou podobu), u každého přechodu je možné definovat Name (název), Comment (komentář) a Graphic (grafickou podobu), pro každou hranu je možné definovat Multiplicity (násobnost), Comment (komentář) a Graphic (grafickou podobu). Po sestavení Petriho sítě se výběrem položky Start Anim-mode zadávají parametry simulace Referesh (obnovení), Duration (trvání) Stepping (posílení) a následně může dojít ke spuštění simulace. Simulace v software Snoopy je velmi přehledná, protože se tokeny přesouvají po jednotlivých hranách a jsou zvýrazněny červenou barvou.

Pro názornost bude nyní uvedeno pracovní prostředí software Snoopy (obr. č. 2).

Obr. č. 2: Pracovní prostředí software Snoopy

5.2 Software Pipe2

Při spuštění software se zobrazí menu a obrazovka rozdělená na dvě části, v jedné části se nachází Analysis Module Manager umožňující rozšířenou analýzu Petriho sítí a druhá část představující pracovní plochu, v níž se Petriho sítí sestavují. Výběrem příslušné položky z menu se sestavují odpovídající prvky Petriho sítě na pracovní plochu, přičemž u každého místa je možné definovat Name (název), Marking (značení), Capacity (kapacita), u každého přechodu je možné definovat Name (název), Rate (sazba) a Timing (časování), pro každou hranu je možné definovat Multiplicity (násobnost). Po sestavení Petriho sítě se definuje přechod, po němž dojde k ukončení simulace, a následně může dojít ke spuštění simulace. Při simulaci v software Pipe2 nedochází k viditelnému přesunu tokenů po hranách, pouze se mění počty tokenů v jednotlivých místech, což snižuje přehlednost.

Pro názornost bude nyní uvedeno pracovní prostředí software Pipe2 (obr. č. 3).

Obr. č. 3: Pracovní prostředí software Pipe2

6. Aplikace P/T Petriho sítě na řešení úlohy o modelování koordinace linek MHD

Jedním z možných způsobů řešení uvedeného problému je graficky založený model, kdy přechody představují zastávky, místa jízdu vozidla mezi zastávkami a tokeny představují vozidla.

Níže uvedený graficky založený model vychází z předlohy fiktivní dopravní sítě s okružním systémem tras linek MHD, které mají společnou přestupní zastávku v centru. Schéma sítě linek MHD modelové sítě je znázorněno na obr. 4. Celkový počet zastávek v síti činí 25, linka č. 1 obsluhuje 9 zastávek, linka č. 2 obsahuje 11 zastávek a linka č. 3 zahrnuje 7 zastávek.

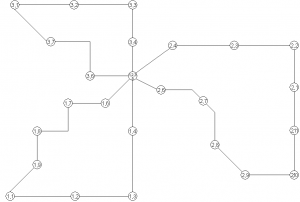
Obr. č. 4. Předlohová dopravní síť MHD

Čísla přiřazená jednotlivým uzlům reprezentují číslo linky, která příslušnou trasu obsluhuje a pořadové číslo zastávky.

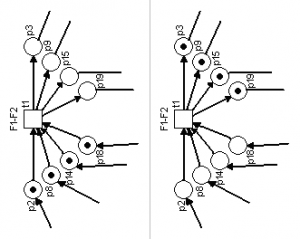
Pro potřeby modelování problému nástroji Petriho sítí se bude každá linka L_i skládat z posloupnosti přechodů (x_i1, x_i2, …, x_ij) a míst, která jsou spojeny hranami, jak je uvedeno na obr. č. 5. Jednotlivé přechody reprezentují zastávky, přechod x_i1 je výchozí zastávkou, x_i5 představuje přestupní zastávku. Přechody x_ip a x_io představují propojení přestupních zastávek. Místa y_ij mezi těmito přechody představují pohyb vozidel mezi zastávkami. Místa označená p_i spojují linky L_i a L_i+1. Jejich prostřednictvím je možné modelovat pohyb cestujících, kteří chtějí přestoupit mezi dvěma spoji dvou linek.

Tokeny v Petriho síti budou mít dva významy. Jednak budou modelovat pohybující se vozidlo a potom také skupiny cestujících, kteří budou v přestupním uzlu přestupovat. V případě místa pi představuje token všechny cestující čekající na přestupní zastávce. V modelu dopravní sítě MHD se mohou vyskytovat různé varianty, buď je aktivován přechod reprezentující přestup cestujícího na spoj jiné linky nebo je aktivován přechod, který představuje že cestující nepřestupuje na spoj druhé linky.

Vzhledem k tomu, že v Petriho síti přechody x_ip a x_io představují propojení přestupních zastávek a nereprezentují zastávky bude počet přechodů na jednotlivých linkách v modelu dopravní sítě MHD o 2 přechody vyšší než je počet zastávek na jednotlivých linkách. To znamená, že celkový počet přechodů na jednotlivých linkách bude činit 33.

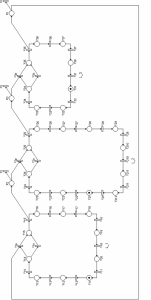
Obr. č. 5: Grafické znázornění Petriho sítě pro řešený problém

Přestupy cestujících modelují v navržené Petrino síti specifické komponenty. Příklad takové komponenty je uveden na obr. č. 6.

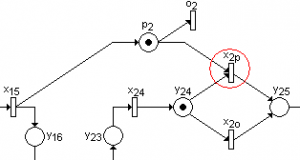
Obr. č. 6: Fragment modelu Petriho sítě znázorňující požadavek přestup

V případě, že cestující budou požadovat přestoupit mezi dvěma spoji dvou linek, bude tento požadavek znázorněn setrváním tokenu ve vstupním místě p_i představujícím všechny cestující, kteří chtějí přestoupit. To znamená, že v případě výskytu tokenu ve druhém vstupním místě y_i4 bude splněna vstupní podmínka pro provedení přechodu x_ip s vyšší prioritou a dojde k jeho aktivaci. V případě požadavku na přestup bude tedy zajištěna provázanost s odjezdem autobusu na přestupní zastávce prostřednictvím přechodu x_ip, který bude aktivován pouze v případě splnění vstupních podmínek.

Jestliže cestující nebudou potřebovat přestoupit, bude aktivován přechod o_i a v místě p_i se nebude vyskytovat token reprezentující přestupující cestující. V případě výskytu tokenu v místě y_i4 znázorňující vozidlo tak bude splněna jediná vstupní podmínka přechodu x_io a dojde k jeho aktivaci. Tato situace je znázorněna na fragmentu dopravní sítě MHD na obr. č. 7.

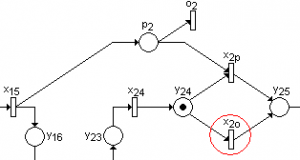
Obr. č. 7: Fragment modelu Petriho sítě bez požadavku na přestup

K modelování Petriho sítí se obecně využívá specializovaných software, např. Snoopy, Pipe2. Provedení simulace umožňuje pozorovat chování navrženého modelu a možné konflikty. Na základě zjištěných skutečností je pak možné změnit konfiguraci modelu. V případě modelu dopravní sítě MHD v Petriho síti se může jednat o modelování návaznosti na přestupních zastávkách.

Postup při potřebě využití Petriho sítí je tedy následující:

V první řadě je třeba sestavit podle zvolené koncepce Petriho sítí model v Petriho síti. Každá Petriho síť se skládá z posloupnosti přechodů a míst spojených orientovanými hranami. Prostřednictvím orientovaných hran se znázorní logické vazby mezi objekty, které jsou vzájemně ovlivněny. K tomu, aby bylo možno modelovat pohyb vozidel, je nutné před začátkem simulace do některého místa na každé lince umístit token představující vozidlo. Token reprezentující cestující, kteří potřebují přestoupit vznikne rozdělením tokenu představujícího vozidlo, který vstoupí do přechodu x_i5 – přestupní zastávky ze kterého vycházejí dvě orientované hrany.

7. Návrh řízení světelné křižovatky Petriho sítěmi

Za účelem dalšího zkoumání byla navržena logika řízení světelné křižovatky prostřednictvím Petriho sítí. Kroky, které je nutné při návrhu logiky řízení světelných křižovatek provést, jsou popsány v následující části příspěvku.

7.1 Analýza vstupních podkladů

Pro návrh logiky řízení světelné křižovatky byly zohledněny následující vstupní podklady: schéma vzorové křižovatky (obr. č.8 ) a fázové schéma (obr. č. 9), prostřednictvím kterého se zajišťují časový intervaly, v nichž mají současně volno určité, zpravidla nekolizní dopravní pohyby na křižovatce. Pro návrh světelného řízení je pochopitelně zapotřebí ještě celá řada údajů, ty však s návrhem řídící logiky nesouvisejí.

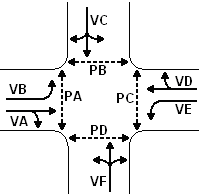
Obr. č. 8: Schéma vzorové křižovatky

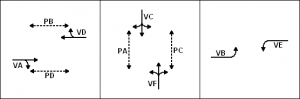
Obr. č. 9: Fázové schéma vzorové křižovatky

7.2 Sestavení Petriho sítě

Před sestavením Petriho sítě byl stanoven význam prvků v zamýšlené Petriho síti. Místa v Petriho síti budou představovat světelné signály na návěstidlech SSZ, přechody v Petriho síti budou představovat okamžiky, při kterých dochází k přepínání světelných signálů, orientované hrany v Petriho síti umožňují realizovat změny stavů a aktuální poloha tokenu bude reprezentovat aktuální návěstní znak.

Při sestavování Petriho sítě se vychází z fázového schématu, v tomto případě se jednalo o fázové schéma uvedené na obrázku č. 9. Nejdříve byla sestavena část Petriho sítě představující první fázi, resp. světelné signály na návěstidlech pro dopravní proudy, které se v první fázi vyskytují, následně byla sestavena část Petriho sítě představující druhou fázi, resp. světelné signály na návěstidlech pro dopravní proudy, které se vyskytují ve druhé fázi a část Petriho sítě představující třetí fázi, resp. světelné signály na návěstidlech pro dopravní proudy, které se vyskytují ve třetí fázi. Na závěr byly části Petriho sítě propojeny tak, aby mohlo docházet ke střídání fází v rámci cyklu.

Sestavená Petriho síť, do které byla doplněna světelná signalizace příslušných světelných signálů v jednotlivých fázích prostřednictvím tokenů (počáteční značení), je uvedena na obrázku č. 10.

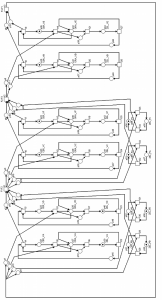
Obr. č. 10: Návrh řídící logiky světelné křižovatky v P/T Petriho síti

Návrh řídící logiky spočívá ve dvou etapách:

1. etapa – návrh správných posloupností jednotlivých světelných signálů na návěstidle.
2. etapa – návrh správných posloupností jednotlivých světelných signálů u jednotlivých návěstidel zajišťující správné přechody mezi fázemi.

V první etapě bylo zajištěno, že po světelném signálu zeleného světla bude zařazen světelný signál oranžového světla a světelný signál červeného světla. Dále bylo zajištěno, že po světelném signálu červeného světla bude zařazen světelný signál oranžového světla a světelný signál zeleného světla. Na obrázku č. 11a a 11b je uvedeno, jak pomocí P/T Petriho sítě navrhnout správnou aktivaci návěstních znaků na návěstidle.

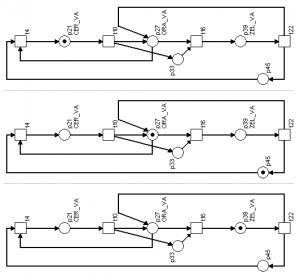
Obr. č. 11a: Změna světelného signálu zeleného světla

Komentář k principu uvedeném na obrázku č. 11a:

Po světelném signálu zeleného světla p39 se prostřednictvím přechodu t22 přesouvá token do místa představujícího světelný signál oranžového světla p27 a doplňujícího místa p45, následně může dojít pouze k přechodu t4, při kterém se token přesouvá do místa představujícího světelný signál červeného světla p21.

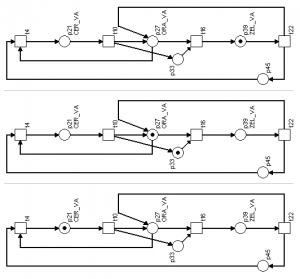
Obr. č. 11b: Změna světelného signálu červeného světla

Komentář k principu uvedeném na obrázku č. 11b:

Po světelném signálu červeného světla p21 se prostřednictvím přechodu t10 přesouvá token do místa představujícího světelný signál oranžového světla p27 a doplňujícího místa p33, následně může dojít k přechodu t16, při kterém se token přesouvá do místa představujícího světelný signál zeleného světla p39.

V popsaných principech se vyskytují doplňující místa p33 a p45, která slouží k tomu, aby v daném časovém okamžiku mohly nastat pouze očekávané přechody, resp. očekávané změny světelných signálů. Nemůže tedy dojít k situaci, že po světelném signálu zeleného světla bude zařazen světelný signál oranžového světla a světelný signál zeleného světla, namísto červeného, resp. k situaci, že po světelném signálu červeného světla bude zařazen světelný signál oranžového světla a světelný signál červeného světla, namísto zeleného.

Kromě částí Petriho sítě zajišťujících správnou řídící logiku týkající se jednotlivých návěstidel v první, druhé a třetí fázi, se v sestavené Petriho síti nacházejí doplňující místa, jež zajišťují správnou funkci logiky řízení světelné křižovatky při přechodech mezi jednotlivými fázemi.

Ve druhé etapě bude zajištěno, aby signály zeleného světla v následující fázi mohly nastat až poté, co v předchozí fázi nastaly signály červeného světla, prostřednictvím principu uvedeného na obrázku č. 12.

Obr. č. 12: Změna fází

Komentář k principu uvedeném na obrázku č. 12:

Současně s umístěním tokenů do míst představujících světelný signál červeného světla pro dopravní proudy, které vyskytují v předchozí fázi, se přesouvají tokeny také do doplňkových míst p2, p8, p14, p18, jež představují vstupní místa přechodu t1. Uskutečněním přechodu t1 je následně realizována změna fází. Po změně fází se nacházejí tokeny v doplňkových místech p3, p9, p15, p19, jež představují výstupní místa přechodu t1 a mohou tak nastat světelné signály zeleného světla pro dopravní proudy, které se vyskytují v následující fázi.

V popsaném principu se vyskytují doplňující místa p2, p8, p14, p18 a p3, p9, p15, p19, která slouží k tomu, aby v daném časovém okamžiku mohly nastat pouze očekávané přechody, resp. očekávané změny světelných signálů při přechodu mezi jednotlivými fázemi.

8. Závěr

Předmětem článku je modelování koordinace linek MHD s využitím Petriho sítí a návrh logiky řízení světelných křižovatek splňující základní princip světelného řízení křižovatek a zajišťující správné přepínání světelných signálů na návěstidlech světelného signalizačního zařízení s využitím software Snoopy a Pipe2.

Vybrané software mají z hlediska ovládání obdobné vlastnosti. Významný rozdíl mezi software se nachází v případě modelovacích schopností, protože software Pipe2 umožňuje stanovení kapacity jednotlivých míst a jednodušší časování jednotlivých přechodů, což může být přínosné především při vytváření složitějších návrhů. Při simulaci vykazuje větší přehlednost a lepší názornost software Snoopy, protože se po hranách přesunují červeně označené tokeny. V případě software Pipe2 se mění pouze počet tokenů v jednotlivých místech Petriho sítě a nedochází k přesunu tokenů po hranách Petriho sítě.

V případě výše uvedeného modelu dopravní sítě MHD v Petriho síti došlo k určitému zjednodušení, v reálném provozu je totiž třeba zohlednit intenzity přepravního proudu, počty a kapacity vozidel, doby oběhů vozidel na jednotlivých linkách. V rámci řešené problematiky se jedná např. o modelování pohybu vozidel v síti linek MHD a zajištění koordinace spojů na přestupních zastávkách. Petriho sítě by tak v budoucnu mohly být využívány při ověřování a hodnocení návrhu dopravní sítě MHD.

Postupným prohlubováním a obohacováním návrhu logiky řízení světelných křižovatek prostřednictvím Petriho sítí, ve kterých bude zohledněna širší množina vstupních podkladů (např. intenzity jednotkových vozidel, trvání světelných signálů), bude možné docílit vytváření signálních plánů v software Pipe2. Petriho sítě tedy mohou nabízet další alternativní způsob, pomocí kterého je možné navrhovat světelné řízení křižovatek.

Použitá literatura

1. [1]ČERNÝ, J., KLUVÁNEK, P. Základy matematickej teórie dopravy. Bratislava: VEDA, 1991. 1. vydání, 279 s. ISBN 80-224-0099-8.
2. [1]ČERNÝ, J., ČERNÁ, A. Teorie řízení a rozhodování v dopravních systémech. Pardubice: Institut J. Pernera, 2004. 1. vydání, 150 s. ISBN 80-86530-15-9.
3. [1]MARKL, J. Petriho sítě I. Ostrava: VŠB-Technická univerzita Ostrava., 2009. 124 s. (Učební texty)
4. [1]KOCHANÍČKOVÁ, M. Petriho sítě. Olomouc: Univerzita Palackého, 2008. 69 s. (Učební texty)
5. [1]JANOUŠEK, V. Modelování objektů Petriho sítěmi. Brno: Vysoké učení technické, 2008. 164 s. (Disertační práce)
6. [1]VONDRÁK, I.: Metody byznys modelování. Ostrava: VŠB-Technická univerzita Ostrava, 2004. (Učební texty)
7. [1]TUREK M.: Návrh světelného řízení křižovatky Dolní – Kralická v Prostějově. Ostrava: VŠB-Technická univerzita Ostrava, 2009. (Diplomová práce)
8. Snoopy. Oficiální stránka. Dostupné na internetu:
   <http://www-dssz.informatik.tu-cottbus.de/index.html?/software/snoopy.html>
9. Pipe2. Oficiální stránka. Dostupné na internetu: <http://pipe2.sourceforge.net>

---

Spoluautorom článku je Ing. Richard Turek, Institut dopravy FS VŠB – TU Ostrava, 17. listopadu 15, 708 33 Ostrava