Fuel consumption analysis of motor vehicle

09. Január, 2013, Autor článku: Matej Juraj, Elektrotechnika
Ročník 6, číslo 1 Pridať príspevok

Paper discuss about the traces of fuel consumption in various operating modes of driving a real vehicle (various included different gears and speed of the vehicle). Also points to the dependence of fuel consumption in l/100km from specific fuel consumption in g/kWh. The calculated values are shown in the plot and compared with the real course measured on the vehicle.

1. Introduction

Today’s engines with electronically controlled fuel injection, not only have significantly higher power, but also significantly lower fuel consumption. The paper presents physical dependence compared with theoretical knowledge and the various dependencies are shown in the plots.

2. Calculation of fuel consumption

Fuel consumption was calculated for the vehicle parameters Seat Ibiza 1.9 TDI 77 kW. The required parameters of engine: maximum power 77 kW/4000 rpm. and torque 250 Nm/1900 rpm. The required parameters of the vehicle: the total mass of 1200/1626 kg, gear ratios of 2.,3. and 4. gear was achieved in experiment. Calculate constants:

c_x=0.33
f_v=0.014
ρ_air=1.22 kg/m³
η_pm=0.93
ρ_fuel=840 kg/m³
S=2m²
α=1
m_v=1200kg
m_p=160kg
g=9.81m/s²
π=3.14
P_vz=F_vz.ν=0.5Sc_xρ_airν³

Forces that must be overcome during driving a vehicle shall be equal to actual force of the driving wheels. Total force must therefore be equal to the force of the driving wheels, see equation (1). The same goes for vehicle’s power needed to overcome the driving forces. Vehicle’s power must be equal to power of the driving wheels and that must be equal to power of engine reduced by efficiency of transmission, see Equation (6).

As can be seen from equation (1), driving vehicle must overcome force of air, rolling, inertia and slope. These forces must be overcome by engine torque, the actual value of engine torque will vary depending on driving forces during driving cycle. In other words, what is the total road load power, so it must be the engine power through a gear ratio and transmission efficiency.

$F_{wheels} = \frac{T_{engine}.i_{total}.\eta_{trans}}{r_d}=F_{total}=$

$F_{air}+F_{rolling}+F_{interia}+F_{slope} (N)$

(1)

Where: T_engine – engine torgue (Nm), i_total – total gear ratio(-), η_trans – efficiency of transmission (-), r_d – Wheel dynamic radius (m), F_air – force of air (N), F_rolling -force of tires rolling (N), F_inertia – force of vehicle inertia, F_slope – force of slope road (N)

In order be able to calculate the total driving force and total driving power of which determine the engine power, we must calculate single running forces by means of the following equations (2), (3), (4), (5). Then we can calculate the actual fuel consumption during driving cycle.
Calculation of driving forces:

Force of air

$F_{air}=\frac{S.c_x.\rho_{air}.\nu^2}{2} (N)$

(2)

Where: S – frontal area of vehicle (m²), c_x – drag coeficient (-), ρ_air – air density (kg/m³), v – vehicle speed (m/s)

Force of rolling

$F_{rolling}=m.g.f_{rolling}.cos(\alpha) (N)$

(3)

Where: m – vehicle mass (kg), g – gravity acceleration (m/s²), f_rolling – coefficient of rolling force (-), α – angle slope road (°)

Force of inertia

$F_{interia}=m.a.\upsilon (N)$

(4)

Where: a – vehicle acceleration (m/s²), ϑ – coefficient of inertia force (-)

Force of slope road calculated according to Equation (5), this force in our calculations are not considered because driving cycle in our simulation is without the slope road, and this force is equal to zero.

$F_{slope}=m.g.sin(\alpha) (N)$

(5)

Once we have calculated all driving forces that must be overcome during the driving cycle, we can calculate the power required to overcome the driving forces and the required engine power, using the Equation (6).

$P_{wheels}=P_{total}=\frac{F_{total}.\nu}{1000}=P_{engine}.\eta_{trans} (kW)$

(6)

If we calculated the engine power needed to overcome forces during driving cycle and know the engine map of brake specific fuel consumptions measured to a dynamometer, Figure 1, we can calculate the fuel consumption of driving vehicle, by equation (7).

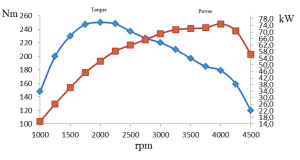
Figure 1: A course of torque and power according to engine speed

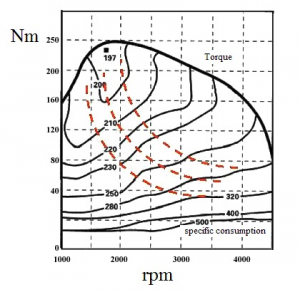
Figure 2: Maximum engine torque and brake specific fuel consumption – bsfc [3]

To calculate runway fuel consumption in liters per 100km is necessary to derive the relationship with specific fuel consumption in the following acts:

$bsfc(g/kW.h) \to FC(l/100km)$

$bsfc\left(\frac{g}{kW.h}\right) \to bsfc.P_{engine}\left(\frac{g}{h}\right) \to \frac{bsfc.P_{engine}}{1000} \left(\frac{kg}{h}\right) \to$

$\to \frac{bsfc.P_{engine}}{1000.\rho_{fuel}} \left(\frac{m^3}{h}\right) \to \frac{bsfc.P_{engine}}{\rho_{fuel}} \left(\frac{l}{h}\right) \to$

$\to \frac{bsfc.P_{engine}}{\rho_{fuel}.\nu} \left(\frac{l}{km}\right) \to \frac{100.bsfc.P_{engine}}{\rho_{fuel}.\nu} \left(\frac{l}{100km}\right) \to$

The resulting equation for the calculation of runway fuel consumption is:

$FC = \frac{100.bsfc.P_{engine}}{\rho_{fuel}.\nu} \left(\frac{l}{100km}\right)$

(7)

Where: bsfc – brake specific fuel consumption (g/kW.h), Pengine – reguired engine power (kW), ρ_fuel – density of fuel (kg/m³), v – vehicle speed (km/h)

Being a diesel engine, maximum torque is with 1900rpm. and further increase in engine speed torque decreases. Conversely it is with an engine power, which from 1000 rpm growing and highest value reached 77 kW at 4000rpm. (Fig. 1). In Fig. 2 shows that the specific fuel consumption is not lowest at high speeds, where grow mechanical losses in the engine and the combustion efficiency decreases. It is not lowest at low speeds, where the heat of combustion discharged cooler (cylinder walls) is in proportion to mechanical work produced by a larger amount of energy fed as fuel at higher engine speeds. The efficiency of the combustion process and decreases again. This shows us that the lowest specific fuel consumption is the higher torque and around 1900 rpm.

In real driving, we measured the individual vehicle fuel consumption in l/100km with the respective speeds of the gears II., III. and IV. in 1500, 2000, 2500, 3000 and 3500 rpm. From the measured data, we have relationships with the above calculated individual driving forces, gear ratios, powers and specific fuel consumption. Enjoyment of these results, we have built in following graphs.

Tab.1: Included gears, vehicle velocity and fuel consumption

gear (v=70km/h)	II.	III.	IV.
Average consumption l/100km	6,46	4,12	3,26
rpm	4000	2450	1650
gear (v=50km/h)	2	3	4
Average consumption l/100km	5,8	3,675	2,6
rpm	2900	1750	1200

The measured data of Tab. 1 shows that in maintaining a constant speed (50 or 70 km / h) and a higher gear shifting are logically the engine speed decreases, so the fuel consumption of vehicles in l/100km also decreases. If you compare just generally measured fuel consumption at both speeds, so we can see that increasing speed increases the fuel consumption.

Tab. 2 Fuel consumption in l/100km with different gear and speed

rpm	1500	2000	2500	3000	3500
II.	4,4	5	5,4	5,7	6
III.	3,3	3,7	4	4,4	5,2
IV.	2,5	3,4	4,5	5,7	6,8

Tab. 3 Vehicle velocity in km/h with different gear and speed

rpm	1500	2000	2500	3000	3500
II.	26	35	45	52	60
III.	44	58	71	85	100
IV.	63	85	105	125	145

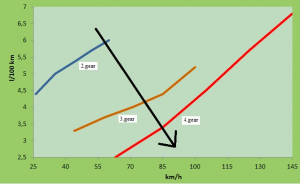
Figure 3: Fuel consumption depending on the vehicle velocity with different gear

Figure 3 shows the dependence of our fuel consumption in l/100 km for the II, III and IV gear. We identify two of his addiction. The first is that higher gear shifting our consumption decreases (arrow).
The dependence of the resulting graph we can prove – after deducting the torque according to the above relations for II, III and IV gear, we built a depending of torque from the engine speed. The depending shows that shifting a higher gear decreases specific fuel consumption g / kWh and also fuel consumption in l/100km. This dependence we blame the relationship for calculation of fuel consumption:

$S_p = \frac{100.m_{pe}.P_{m}}{\rho_{fuel}.\nu} \left(\frac{l}{100km}\right)$

(8)

Considered to be constant: power P_m, speed, density of fuel ρ_fuel ,100, then our only remaining equal, where S_p consumption depends upon the specific fuel consumption m_pe.

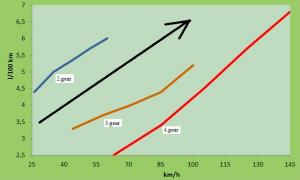
Figure 4: Fuel consumption depending on the vehicle velocity with 2., 3., and 4. gear

In Fig. 4 we see that with increasing vehicle speed, also increases fuel consumption in l/100 km (arrow). After deducting specific fuel consumption for each engine speed, we built a graph of specific fuel consumption and consumption in l/100km the speed in km / h (Fig. 4). Graph has two vertical axes – one of the displayed fuel consumption and other specific fuel consumption.

We can see that increasing the speed of the vehicle specific fuel consumption decreases, but increases fuel consumption in l/100km. This paradoxical phenomenon we can prove the relation (8). Although the specific fuel consumption decreases, the engine power increases by a higher value and increase the total consumption l/100km. Major performance improvement from increasing the speed we can prove for example in power required to force of air:

$P_{vz} = F_{vz}.\nu=0.5 S.c_x.\rho_{air}.\nu^3 (kW)$

(9)

That is, if we increase the vehicle velocity 2 times, so the force of air increases 4 times and the power required to force of air increases 8 times. Therefore, when we increase the vehicle velocity specific fuel consumption decreases engine power is increased several times and that we will increase consumption. As we see in relation to the calculation of fuel consumption (8).

3. Conclusion

In real drive is fuel consumption affected by many factors, eg. driving style, ambient temperature, tire pressure, road gradient, road surface, if the car is empty or fully loaded. But true to the highest driving efficiency (ie low consumption due to the acquired power) will achieve keeping the engine speed in low specific fuel consumption at the optimal load. It means that in the car with five-speed gearbox is very necessary to accelerate the first four levels of speed and low specific fuel consumption, then ranked fifth gear and continue to maintain 1900 rpm.

References

Freiwald, A.: Diagnostika a opravy automobilov II, Žilinská univerzita 2008
Vlk,F.: Diagnostika motorových vozidiel, VLK 2006
http://www.cleanmpg.com/forums/showthread.php?p=130788

Coauthor of this paper is Adrián Laczkó

O časopise

Meta

RSS

Fuel consumption analysis of motor vehicle

Napísať príspevok

Rubriky

Burza práce

Štúdijné materiály

Archív