Optimalizácia parametrov PID regulátora s využitím funkcií fminimax a fminunc realizovaná v prostredí MATLAB Simulink

27. Január, 2014, Autor článku: Ivančin Ivan, MATLAB/Comsol, Študentské práce
Ročník 7, číslo 1 Pridať príspevok

Tento článok je venovaný téme optimalizácie s využitím softvérových nástrojov Global Optimalization Toolbox v prostredí MATLABu. Tento súbor nástrojov je vo veľkej miere využívaný pri riešení rôznych optimalizačných úloh. Článok sa konkrétne venuje funkciám fminimax a fminunc, opisuje algoritmus ich výpočtu a ukazuje rôzne obmedzujúce faktory týchto funkcií. Aplikácia postupov optimalizácie je uskutočnená na príklade optimalizácie parametrov PID regulátora.

Úvod

Hlavným cieľom optimalizácie je hľadanie konkrétnych hodnôt premenných, za účelom získania extrémov cieľovej funkcie. Tieto hodnoty minimalizujú alebo maximalizujú funkciu a vyhovujú vedľajším podmienkam. Pri optimalizačnej úlohe nie je podmienkou definovať vedľajšie podmienky. Väčšina optimalizačných úloh má jednu cieľovú funkciu no existujú i také, ktoré ju nemajú alebo ju majú viacnásobnú. Medzi optimalizačné úlohy, ktoré nemajú túto funkciu patria tie, v ktorých sa snažíme nájsť premenné, ktoré spĺňajú vedľajšie podmienky a teda cieľovú funkciu nie je nutné definovať.

Optimalizácia systému s viacnásobnou cieľovou funkciou je založená na hľadaní premenných za účelom nájdenia extrémov dvoch a viacerých funkcii. V praxi sa tieto systémy pretransformovávajú pomocou lineárnej kombinácie cieľových funkcii na optimalizačný problém s jednou cieľovou funkciou. Stretávame sa aj s možnosťou transformácie cieľových funkcii do vedľajších podmienok.[1] Vyšetrovanie extrémov funkcie, teda hľadanie minima či maxima, sa používa v mnohých odvetviach. V týchto časoch sa postupy optimalizácie a tým aj riešenie optimalizačných metód využívajú:

nastavenie fyzikálnych systémov za účelom minimalizovania spotrebovanej energie a maximalizovania efektívnosti
výrobné podniky za účelom minimalizácie výrobných nákladov a maximalizácie výkonnosti výroby
investičné subjekty za účelom minimalizovania risku a maximalizovania zisku portfólia
navigácie za účelom minimalizácia nákladov a času stráveného transportom medzi bodmi trasy pri výbere cesty
dizajnéri pri návrhu súčiastky či systému za účelom minimalizácie použitého materiálu, času výroby pri spĺňaní vedľajších podmienok ako napríklad odolnosť voči tlaku a ťahu

Global Optimization Toolbox

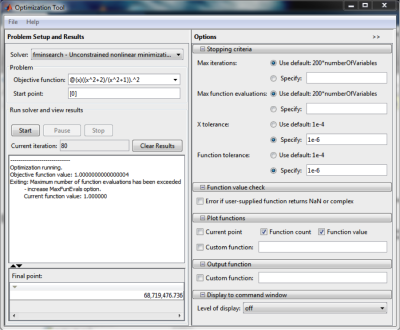
GOT nám poskytuje metódy, ktoré vyhľadávajú globálne riešenia problémov, ktoré obsahujú viacnásobné maximá alebo minimá. To zahŕňa globálne vyhľadávanie, multistart, solvery vyhľadávania vzorov a genetické algoritmy. Tieto postupy môžeme použiť pri riešení optimalizačných problémov, kde objekt alebo cieľová funkcia môže byť spojitá, nespojitá, stochastická alebo nemá derivácie, či obsahuje simulácie alebo Black-box funkcie s nedefinovanými hodnotami pre niektoré parametre nastavenia. Geneticke algoritmy a solvery vyhľadávania vzorov podporujú algoritmické upravovanie. Za pomoci GOT môžeme vytvoriť vlastnú genetickú variantu algoritmu modifikáciou počiatočnej populácie a nastavením fitnes škálovania alebo definovaním rodičovského výberu, krížením a mutáciou funkcií. Samotné riešenie optimalizačných úloh sa realizuje cez Optimization Tool (viď obrázok č.1).

Obrázok 1: Optimization Tool

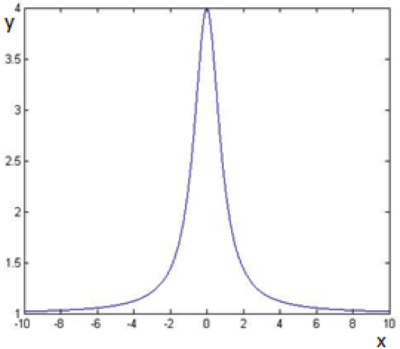
V tomto prípade sa použila metóda na vyhľadanie minima cieľovej funkcie fminsearch, algoritmus bol aplikovaný na funkciu:

$F(x) = \left ( \frac{x^2+2}{x^2+1} \right )^2$

(1)

so štartovacím bodom 0. Výstupom z tejto metódy bol bod x_kon=68719476736, v ktorom dosiahla funkcia hodnotu F_{x_kon}=1.0000000000000004 . Optimalizácia sa ukončila z dôvodu obmedzenia počtu evaluácií (MaxFunEvals=200) ako je to zobrazené na Obrázku číslo 2. Výpočet trval 80 iterácii.

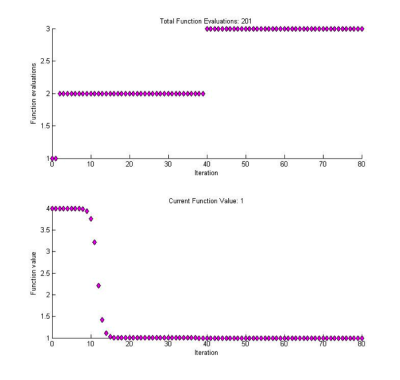
Obrázok 2: Grafický výstup z Optimization Toolu

Funkcia fminimax

Táto optimalizačná metóda hľadá minimum z maximálnej hodnoty vektorovej funkcie s vedľajšími podmienkami. fminimax vnútorne preformulováva minimax problém do ekvivalentného problému Nelineárneho lineárneho programovania. Táto funkcia využíva metódy sekvenčného kvadratického programovania (SQP) na vyriešenie optimalizačného problému.

$min \; max \; F_{i(x)}$

(2)

Vedľajšie podmienky:

$c(x) \leq 0$

$ceq(x) = 0$

$A*x \leq b$

$Aeq*x=beq$

$lb \leq x \leq ub$

(3)

kde b a beq sú vektory, A a Aeq sú matice, c(x), ceq(x), F(x) sú funkcie ktoré vracajú vektory. F(x), ceq(x), c(x) môžu byť aj nelineárnymi funkciami. x, lb a ub môžu byť zadané ako vektory či matice. Touto funkciou sa dajú riešiť aj max-min optimalizačné úlohy, po úprave:

$min \; max \; F_{i(x)} = -min \; max \; (-F_{i(x)})$

(4)

Metóda fminimax môže minimalizovať iba spojité funkcie a na výstupe sa môžu nachádzať iba lokálne minimá.

Funkcia fminunc

Táto optimalizačná metóda hľadá minimum nelineárnej funkcie viac premenných bez vedľajších podmienok kde x je vektor a f(x) je skalárna funkcia. Metóda dovoľuje použiť aj nelineárnu funkciu. Táto optimalizačná úloha sa vo všeobecnosti nazýva ako nelineárna optimalizácia bez vedľajších podmienok.

$min_x = f(x)$

(5)

Pri tejto metóde sa dá nastaviť jeden z dvoch možných algoritmov výpočtu, „quasi-newton“ alebo „trust-region“. Metóda fminunc minimalizuje len spojité funkcie, pričom môže vyhodnotiť len lokálne minimum. fminunc minimalizuje len nad množinou reálnych čísel, teda x musí patriť do tejto množiny a taktiež funkcia f(x) môže mať na výstupe len čísla patriace do tejto množiny. Pokiaľ sa na vstupe nachádza komplexné číslo, musí byť zadané v tvare x=a+j*b.

Príklad

V tomto článku sa venujeme dvom funkciám, fminimax a fminunc. Prácu týchto metód budeme demonštrovať na príklade optimalizácie PID regulátora sústavy tretieho rádu. Prenosová funkcia regulovaného systému bola:

$F(s)=\frac{1,5}{50*s^3+43*s^2+3*s+1}$

(6)

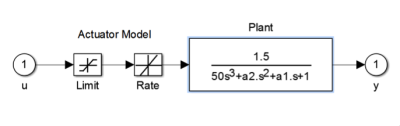
Obrázok 3: Bloková schéma regulovaného systému

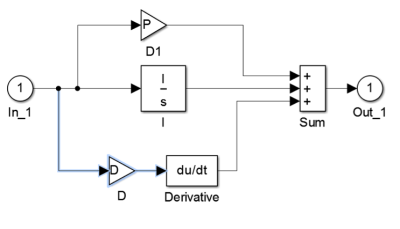
Systém bol naprogramovaný v prostredí MATLAB-Simulink. Výsledná schéma uzatvorenej regulačnej slučky systému:

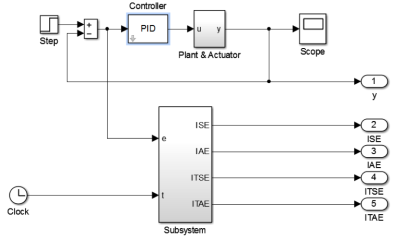
Obrázok 4: Bloková schéma uzavretej regulačnej slučky

Optimalizačná úloha spočívala v nastavení hodnôt PID regulátora Kp,Kd a Ki.

Obrázok 5: PID regulátor

Pri vypracovávaní a riešení danej úlohy sme využili integračné kritéria stability. Tieto kritéria sa v praxi využívajú pri odlaďovaní a optimalizácii PID regulátorov v uzavretej regulačnej slučke. V riešení problému využívame kritéria ISE(The Integral of Squared Error), IAE (The Integral of Absolute Error), ITSE (The Integral of Time Multiply Squared Error), ITAE (The Integral of Time multiply Absolute Error). [5]

$I_{ISE}=\int_0^{\infty} e^2 (t)dt$

$I_{IAE}=\int_0^{\infty} |e(t)| dt$

$I_{ITSE}=\int_0^{\infty} t*e^2 (t)dt$

$I_{ITAE}=\int_0^{\infty} t*|e(t)|dt$

(7)

Ako štartovací bod optimalizačných metód bol zadaný vektor parametrov regulátora:

$Kp=0,63$

$Ki=0.0504$

$Kd=1.9688$

(8)

Pri takto zadaných parametroch bola prechodová charakteristika odpozorovaná zo simulácie:

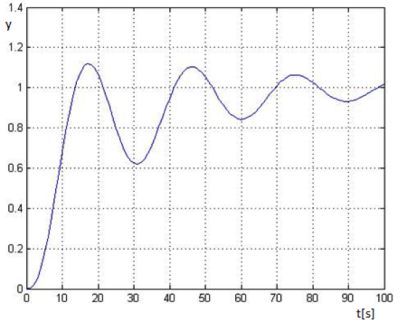
Obrázok 6: Prechodová charakteristika PID

Prvou metódou použitou na nájdenie optimálneho nastavenie PID regulátora bola fminimax. Po piatich iteráciách bol výstupom vektor s nasledujúcimi parametrami regulátora:

$Kp= 0.5559$

$Ki=0.0608$

$Kd=5.2939$

(9)

V tomto nastavení systému bolo zaznamenaná nasledujúca prechodová charakteristika:

Obrázok 7: Prechodová charakteristika systému, fminimax

Ten istý systém a teda aj optimalizačnú úlohu sme dali na vstup druhej funkcie, fminunc. Keďže táto metóda ponúka dva typy algoritmov pre nájdenie optimálnej konštelácie parametrov regulátora, boli použité oba Trust-region aj Quasi-Newton. Prvým použitým algoritmom bol Quasi-Newton:

$Kp= 2.8064$

$Ki= 0.1273$

$Kd=13.1228$

(10)

S takto nastavenými parametrami sme odpozorovali prechodovú charakteristiku:

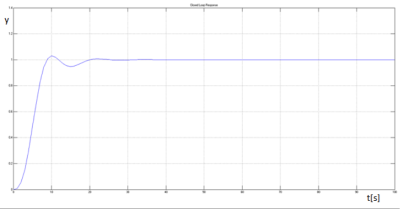
Obrázok 8: Prechodová charakteristika systému, fminunc, quasi-newton

Pri použití algoritmu Trust-region boli finálne parametre regulátora optimalizované na hodnoty:

$Kp= 2.0751$

$Ki=0.1245$

$Kd= 10.5689$

(11)

S takto nastavenými parametrami sme odpozorovali prechodovú charakteristiku:

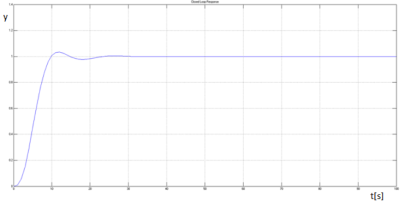
Obrázok 9: Prechodová charakteristika systému, fminunc, trust-region

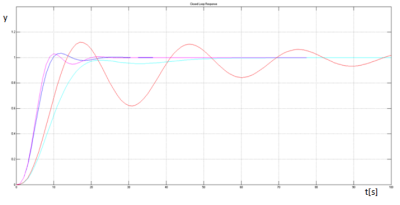
Obrázok 10: Prechodové charakteristiky systému

Záver

Tento článok referoval o optimalizácii a jej implementácii v prostredí MATLAB a o riešení optimalizačných úloh pomocou softvérových nástrojov v Global Optimization Toolboxe. Článok sa bližšie venoval dvom optimalizačným funkciám, fminimax a fminunc. Funkcionalita týchto funkcií bola demonštrovaná na príklade optimalizácie parametrov PID regulátora v uzavretej regulačnej slučke(viď obrázok č.4). Funkcia fminimax mala najlepší priebeh v ohľade preregulovania systému, no čas regulácie bol pri použití tejto metódy najdlhší (viď obrázok č.10). Pri použití funkcie fminunc bol priebeh oboch použitých algoritmov porovnateľný. Pri použití algoritmu quasi-Newton dosahovala optimalizácia najlepšie úspechy, tento fakt sa dal odsledovať na priebehu v ktorom sme zaznamenali menšie preregulovanie a lepšiu dynamiku regulácie ako pri príklade použitia algoritmu trust-region (viď obrázok č.10).

Použitá literatúra

Róbert Bartko: MATLAB II. Optimalizácia, Vydavatelství VŠCHT , Praha 2008, ISBN 978-80-7080-691-3
Solve fminimax constraint problem, URL:
http://www.mathworks.com/help/optim/ug/fminimax.html#f187532
Using fminimax with Simulink Model- MATLAB & Simulink, URL:
http://www.mathworks.com/help/optim/ug/example-using-fminimax-with-a-simulink-model.html
Find minimum of unconstrained multivariable function- MATLAB fminunc, URL:
http://www.mathworks.com/help/optim/ug/fminunc.html
Yi Cao, Learning PID Tuning III: Performance Index Optimization, 8.2.2008, URL:
http://www.mathworks.com/matlabcentral/fileexchange/18674-learning-pid-tuning-iii-performance-index-optimization/content/html/optimalpidtuning.html
Unconstrained Nonlinear Optimization Algorithms, URL:
http://www.mathworks.com/help/optim/ug/unconstrained-nonlinear-optimization-algorithms.html#f3137
Constrained Nonlinear Optimization Algorithms, URL:
http://www.mathworks.com/help/optim/ug/constrained-nonlinear-optimization-algorithms.html#f26684
Choosing a solver, URL:
http://www.mathworks.com/help/optim/ug/choosing-a-solver.html#brhkghv-19

Spoluautorkou článku je Tatiana Mudráková

O časopise

Meta

RSS

Optimalizácia parametrov PID regulátora s využitím funkcií fminimax a fminunc realizovaná v prostredí MATLAB Simulink

Napísať príspevok

Rubriky

Burza práce

Štúdijné materiály

Archív