V článku je podrobne rozpracovaný šesť kanálový deskriptor (6KD) textúr. Podrobne analyzujeme jeho vnútornú stavbu a princíp jeho činnosti. Uvedený deskriptor obrazových textúr vychádza z analýzy a porovnania vlastnosti obrazových textúr v oblasti detailových koeficientov diskrétnej waveletovej transformácie (DWT). Deskripcia je vykonaná na báze DWT rozkladu, prahovania detailových koeficientov a následného generovania histogramov jednotlivých prahovaných kanálov. V článku je experimentálne overená funkčnosť daného deskriptora pre klasifikáciu obrazových textúr. Sú analyzované jeho vlastnosti ako je citlivosť na zmenu energie obrazových textúr. Tiež je experimentálne overená schopnosť klasifikácie textúr štandardnej databázy po ich rotácii a škálovaní. V závere je vyhodnotená účinnosť 6KD v porovnaní s 9KD.

1. Úvod

Deskripcia textúr [1] má praktické využitie v mnohých aplikačných a vedeckých odvetviach. V meteorológii sa používa pri analýze a spracovaní družicových snímok, ďalej má využitie pri kontrole kvality rôznych výrobkov, ako je kvalita ovocia, papiera alebo technických súčiastok. Veľké uplatnenie má aj v medicíne pri analýze ultrazvukových a rtg. snímok, ale aj pri zisťovaní zrakových ochorení. Tiež je využívaná pre rozpoznávanie tvári [2] alebo zvislého dopravného značenia [3]. Jednou z možnosti aplikácie je aj optické rozpoznávanie textu (OCR – Optical Character Recognition). Medzi základné metódy popisovania textúr patria štatistické, geometrické, modelovo orientované metódy, metódy založené na priestorovo-frekvenčnej analýze [4, 5, 6] a iné metódy ako napríklad SIFT (Scale Invariant Feature Transformation) [7].

Vyššie uvedené metódy majú svoje výhody ako aj nevýhody. Napríklad štatistické metódy sú veľmi jednoducho implementovateľné ale pomerne málo presné. Metóda SIFT je síce presná a nezávislá na škále porovnávaných obrazov ale jej implementácia je veľmi náročná na výpočtový výkon a čas. V tomto príspevku sa budeme zaoberať analýzou a popisovaním textúr v priestorovo frekvenčnej oblasti. Pre tento účel bude podrobne popísaný algoritmus 6 kanálového deskriptora (6KD), ktorý analýzu uskutočňuje na základe subpásiem diskrétnej waveletovej transformácie (DWT) textúry [8, 9]. Pre účely vyhodnocovania účinnosti analyzátorov textúr sú textúry začleňované do databáz obrazových textúr. Pre účely experimentalného vyhodnotenia vlastnosti navrhnutého 6KD budeme využívať štandardnú databázu (ŠD) [10, 4] Budeme sa zaoberať vplyvom zmeny energie na citlivosť tohto 6KD. V závere je vyhodnotená účinnosť popisovania textúr uvedeného 6KD so zmenenou mierkou či rotáciou oproti textúram zo ŠD.

2. 6KD pre popisovanie obrazových textúr v priestore DWT

6KD tak ako aj 9-kanálový deskriptor (9KD) [11] je založený na princípe využitia 9 waveletových subpásiem ale tieto sú na rozdiel od 9KD zlúčené do 6 kombinovaných subpásiem. Z uvedeného vyplýva, že pre činnosť tohto 6KD je potrebné vstupnú textúru rozložiť do troch úrovní DWT [12]. Jednotlivé subpásma okrem subpásma aproximačných koeficientov – ³LL, sa sčítaním rozkladových koeficientov zlúčia do kombinovaných subpásiem. Pred samotným zlúčením sú subpásma vyšších úrovní interpolované na veľkosť subpásiem prvej úrovne. Interpolácia je rovnako ako pre 9KD dosiahnutá opakovaním hodnoty rozkladového koeficienta v horizontálnom a vertikálnom smere [11].

Prvý kanál 6KD vznikne sčítaním jednotlivých spektrálnych koeficientov z už rozšírených subpásiem ³HL,³HH,³LH, druhý kanál sčítaním ²HL,²HH,²LH a tretí kanál sčítaním ¹HL,¹HH,¹LH. Tieto kombinované kanály (1, 2, 3) sú nemenné pre rotáciu. Štvrtý kanál 6KD vznikne kombinovaním subpásiem ³HL,²HL,¹HL, piaty kombináciou ³HH,²HH,¹HH a šiesty je súčtom ³LH,²LH,¹LH. Tieto kanály (5, 6, 7) sú nemenné pre škálovanie. Toto je ilustrované blokovou schémou 6KD na Obr. 1.

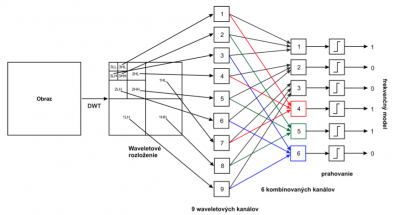
Obr. 1 Bloková schéma 6-kanálového deskriptora

Koeficienty takto získaných šiestich kanálov sú následne prahované, teda ak hodnota koeficientu prevyšuje stanovenú hodnotu prahu prideľuje sa hodnota logickej 1, a ak je pod hodnotou prahu pridelí sa logická 0. Zo štatistických vlastnosti popisovaných textúr a s ohľadom na rozsah hodnôt, ktoré spektrálne koeficienty v jednotlivých kanáloch nadobúdajú vyplýva, že pre jednoduché zovšeobecnenie danej metódy je pre všetky textúry možné zvoliť nulovú prahovú hodnotu [11]. Počet rôznych možných frekvenčných modelov pre 6KD je 2⁶=64 a počet opakovaní jednotlivých frekvenčných modelov opäť závisí od veľkosti vstupnej textúry. Vo všeobecnosti je počet opakovaní možné určiť takto

(1)

kde k je počet opakovaní, N a M sú horizontálny a vertikálny rozmer analyzovanej textúry. Výstupom zo 6KD je histogram, ktorý udáva počet výskytu jednotlivých frekvenčných vzorov v percentách. Kódové slová možných frekvenčných vzorov sú prevedené z binárnej do desiatkovej sústavy, čiže im zodpovedajú hodnoty od 0 po 63. Pre ukážku výstupu zo 6KD je na Obr. 2 uvedený histogram textúry 1.1.01 zo štandardnej databázy [4]. Keďže výskyt jednotlivých frekvenčných vzorov nepresiahol pri textúrach s rozmerom 512×512 hodnotu 10%, tak je vo výslednom histograme na zvislej osi zobrazená len časť od 0% po 10%.

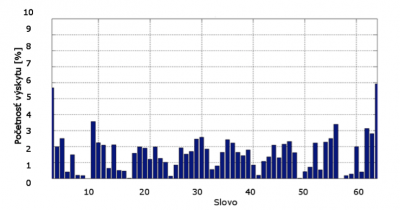
Obr. 2 Histogram výstupu 6KD pre textúru s označením 1.1.01

3. Citlivosť 6K deskriptora na zmenu energie a rotáciu textúry

V nasledujúcej kapitole bude sledovaný vplyv zmeny energie a rotácie textúry na citlivosť 6KD. Analyzované budú dve textúry ŠD s označením T_1 a T_2. Na Obr. 3(a) je uvedená textúra T_1, ktorá je na
Obr. 3(b) rotovaná o 45° a na Obr. 3(c) je škálovaná o 200%. Analogicky je na Obr. 4(a c) zobrazená textúra T_2.

Obr. 3 Textúra T_1 (a) rotovaná o 45° (b) a škálovaná o 200% (c)

Obr. 4 Textúra T_2 (a) rotovaná o 45° (b) a škálovaná o 200% (c)

Energia textúry je daná ako suma kvadrátov obrazových prvkov textúry a energia po DWT ako suma kvadrátov jednotlivých rozkladových koeficientov [11]. Celková energia v obrazoch rádovo nadobúda hodnoty prevyšujúce 1×10⁹, preto v jednotlivých experimentoch budú výsledné hodnoty energie normované hodnotou 1×10⁶. Citlivosť 6KD na zmenu energie pri rotácii a škálovaní textúr v jednotlivých kanáloch bola overená na textúrach T_1 a T_2. Energie v jednotlivých kanáloch sú počítané už po rozšírení subpásiem na rovnakú veľkosť. Výsledky pre obe textúry sú uvedené v Tab. 1.

Tab. 1 Kanálové energetické zmeny vplyvom rotácie, škálovania a transformácie textúry T_1 a T_2

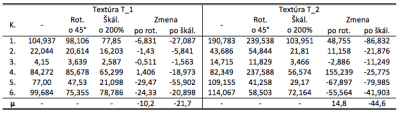
V prípade 6KD je na základe Tab. 1 možné usúdiť, že pre rotovanú textúru T_1 v 4. kanále sa energia zvýšila a v ostatných došlo k zmenšeniu energie. Pri rotovanej textúre T_2 je v Tab. 1 možné tiež pozorovať nárast energie, v kanáloch 1, 2 a 4 a v ostatných sa energia opäť oproti pôvodnej textúre zmenšila. V prípade škálovaných textúr T_1 a T_2 je v Tab. 1 vidieť, že voči energii pôvodnej textúry sa energia vo všetkých pásmach zmenšila. V Tab. 1 je tiež uvedená priemerná zmena energie µ.

V Tab. 2 sú uvedené hodnoty celkovej energie kanálov, stredné hodnoty energetických zmien pre škálovanú a rotovanú textúru T_1 a T_2. Pre porovnanie sú tieto hodnoty uvedené pre šesťkanálový a deväťkanálový deskriptor. Z Tab. 2 je zrejmé, že pomer medzi energiou kanálov a strednou hodnotou zmien energie (µ) vyjadrený v percentách je pre oba modifikácie vyšší pri 6KD. Z uvedeného teda vyplýva, že tento deskriptor je na zmenu energie citlivejší.

Tab. 2 Celkové energetické zmeny vplyvom rotácie, škálovania a transformácie textúry T_1 a T_2

4. Účinnosť 6KD

Pri overovaní možnosti aplikácie 6KD boli vykonané nasledujúce experimenty. Bola testovaná schopnosť tohto deskriptora priradiť najviac podobnú textúru zo štandardnej databázy k vstupnej popisovanej textúre. Ďalej ako bola vstupná textúra škálovaná z verzie textúry ŠD. V poslednom experimente je na vstup 6KD privedená škálovaná textúra ŠD. Účinnosť 6KD bude vyhodnocovaná pomocou strednej kvadratickej chyby (MSE), ktorá je daná vzťahom

(2)

kde je početnosť výskytu i-tého frekvenčného modelu zo vstupnej textúry, je početnosť výskytu i-tého frekvenčného modelu štandardnej textúry, N je počet rôznych možných frekvenčných modelov ( pre 6KD N = 64).

Je zrejmé, že textúra ŠD s najmenšou hodnotou MSE bude vyhodnotená ako textúra, ktorá najlepšie zodpovedá charakteru vstupnej textúry. Na Obr. 5 je zobrazená textúra, ktorá bude popisovaná pomocou 6KD. Ide o textúru kôry stromu. Táto textúra nie je súčasťou ŠD. Cieľom experimentu je zistiť aké budú stredné kvadratické chyby histogramov výstupu 6KD a či MSE textúr kôr bude mať nižšiu hodnotu ako MSE ostatných textúr.

Obr. 5 Popisovaná textúra

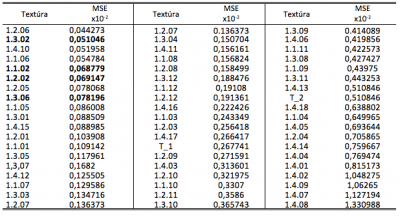
V Tab. 3 sú uvedené názvy textúr ŠD a hodnoty MSE medzi histogramom výstupu 6KD týchto textúr a vstupnej textúry. Hrubým písmom sú zvýraznené bunky, ktoré zodpovedajú textúram kôry a tabuľka je zoradená podľa hodnoty MSE. Z Tab. 3 je zrejmé, že najnižšia hodnota MSE zodpovedá textúre s označením 1.2.06. Táto textúra však nezodpovedá textúre so štruktúrou kôry. Z Tab. 3 tiež možno vidieť, že viaceré textúry, ktoré nemajú štruktúru kôry majú hodnotu MSE nižšiu ako textúr s kôrou. Druhú najmenšiu MSE mala textúra 1.3.02, ktorá patrí medzi kôry a je aj vizuálne najviac podobná k vstupnej textúre.

Najväčšiu strednú kvadratickú chybu z kôr mala 1.2.02, ktorá patrí medzi histogramovo vyrovnané textúry, histogramovo nevyrovnaná verzia tejto textúry 1.1.02 mala o niečo menšiu MSE. Podobnosť histogramov frekvenčných modelov textúr kôry je zobrazená na Obr. 6. Z hľadiska výberu najviac podobnej textúry pomocou deskripcie so 6KD sa vyskytla jedna chybná detekcia, a to 1.2.06. Ak by sme deskripciu vykonávali s cieľom priradiť ku vstupnej textúre všetky štruktúry kôry zo ŠD, vyskytli by sa dve ďalšie chybné detekcie, a to 1.1.06 a 4.1.10. Prvých 6 detekcii aj s prislúchajúcimi MSE je vizuálne zobrazených na Obr. 7.

Tab. 3 MSE histogramov frekvenčných modelov textúr zo ŠD počítaná voči histogramu vstupnej textúry pre 6KD

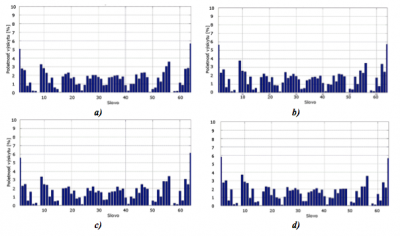
Obr. 6 Histogram frekvenčných modelov 6KD pre a) vstupnú textúru, b) textúru 1.1.02, c) textúru 1.3.02 a d) textúru 1.2.02

Obr. 7 Prvých 6 detekcii s najnižším MSE

V ďalšom experimente bola ŠD rozšírená o textúru tejto databázy 1.5.2_00 (Obr. 8) , ktorá je podrobená rotácii a takému škálovaniu, ktoré zabezpečí to, že rotovaná textúra bude zväčšená tak, aby s rozmerom identickým ako pred škálovaním neobsahovala nedefinované miesta. Časti textúry, ktoré po škálovaní presahujú stanovený rozmer budú orezané. Textúra bola rotovaná o 30°, 60°, 90°, 120°, 150° a 200°. Rovnako ako v predchádzajúcom experimente aj v tomto bude účinnosť vyhodnotená na základe hodnoty MSE.

Obr. 8 Textúra 1.5.02_00, ktoréj rodtácie sú doplnené do ŠD

V Tab. 4 sú hodnoty MSE zoradené a hrubým písmom sú zvýraznené textúry rozšírenej ŠD zodpovedajúce textúram kôry.

Tab. 4 MSE histogramov frekvenčných modelov textúr z rozšírenej ŠD počítaná voči histogramu vstupnej textúry 1.5.02_00 pre 6KD

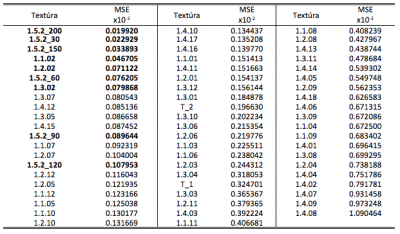
Z výsledkov uvedených v Tab. 4 je vidieť, že z hľadiska priradenia rotovaných textúr k vstupnej textúre, hodnoty MSE pre 6KD sú v tomto poradí. Najmenšiu hodnotu ma 1.5.2_200, po nej nasledovala 1.5.2_30, 1.5.2_150. Ďalej nasledujú textúry, ktoré zobrazujú štruktúru kôry a preto ich nemožno vyhodnotiť ako jednoznačne chybné detekcie. To isté platí pre textúru 1.3.02 nasledujúcu po správnej detekcii rotovanej textúry 1.5.2_60. Tieto textúry sú uvedené na
Obr. 9. Ostatné textúry medzi, ktoré majú nižšie MSE ako rotácie textúry 1.5.2_00 predstavujú chybné detekcie. Uvedené textúry okrem textúr 1.1.02, 1.2.02 a 1.3.02 sú zobrazené na Obr. 10.

Obr. 9 Textúry kôr, ktorých MSE histogramov frekvenčných modelov je nižšie ako MSE pre rotácie textúry 1.5.02_00

Obr. 10 Textúra 1.5.02_00 , jej rotácie a chybné detekcie s uvedenou hodnotou MSE

5. Porovnanie 6K a 9K deskriptorov

V predchádzajúcich kapitolách boli teoreticky analyzované vlastnosti 6KD a tiež bola vyhodnotená jeho účinnosť. Táto účinnosť bola vyhodnotená v dvoch experimentoch. Prvý sa zameriaval na vyhľadávanie textúr, ktoré si sú svojou štruktúrou podobné a druhý bol zameraný na vyhodnotenie účinnosti pri vyhľadávaní textúry, ktorá bola rotovaná a škálovaná. Rovnaké experimenty boli vykonané aj pre 9KD [11]. Teraz v stručnosti porovnáme dosiahnuté výsledky oboch deskriptorov, ktoré sú uvedené v Tab. 5.

Tab. 5 Porovnanie výsledkov dosiahnutých pomocou 6KD a 9KD

Z dosiahnutých výsledkov vyplýva, že každý z deskriptorov sa hodí na porovnávanie iného druhu. Pri priradení najviac podobnej textúry zo ŠD k vstupnej textúre obidva deskriptory dosahujú porovnateľné výsledky. Pri výbere všetkých textúr zo ŠD zodpovedajúcich vstupnej textúre 6KD svojou účinnosťou výrazne prevyšuje 9KD. Pri priradení rotovaných textúr zo ŠD zodpovedajúcich vstupnej textúre dosiahol lepšie výsledky 9KD a tiež pri nájdení textúr prislúchajúcich vstupnej textúre, ale v iných mierkach sa javí byť výhodnejšie použiť 6KD.

6. Záver

V tomto článku bol rozpracovaný algoritmus popisovania textúr pomocou 6KD, ktorý textúry popisuje na základe rozkladových koeficientov DWT. Tento deskriptor bol podrobne uvedený a na základe experimentov boli vyhodnotené jeho vlastnosti. Pritom sme zistili, že pri škálovaní textúr sa energia vo všetkých kanáloch 6KD zmenšila, a to v prípade T_1 aj T_2. Pri experimentoch so správnym priradením textúry zo ŠD k vstupnej textúre 6KD ako aj 9KD majú svoje výhodné aj nevýhodné vlastnosti. Ak ide o výber najviac podobnej textúry, viac sa osvedčil 9KD, ktorý ju priradil správne. 6KD priradil najmenšiu MSE nesprávnej textúre, ktorá medzi kôry nepatrí. Ak sme však chceli zo ŠD vybrať všetky štruktúry vstupnej textúry, v našom prípade všetky textúry kôry, osvedčil sa viac 6KD, ktorý priradil všetky 3 kôry z databázy s troma chybnými detekciami.

9KD našiel len najviac podobnú kôru z databázy a za ňou priradil 29 nesprávnych textúr, ktoré mali menšiu MSE ako najväčšia z kôr. Pri správnom priradení rotovaných textúr zo ŠD k vstupnej textúre sa viac osvedčil 9KD, ktorý správne identifikoval vstupnú textúru vo všetkých uhloch rotácie. 6KD nedokázal správne priradiť zodpovedajúce textúry, vyskytlo sa pri ňom 6 chybných detekcii. V prípade priradenia tých textúr kôry zo ŠD, ktoré majú inú mierku ako vstupná kôra, bol presnejší 6KD, priradil zodpovedajúce textúry bez rušivých. 9KD zasa nedokázal presne určiť textúry inej mierky, vyskytli sa pri ňom 4 chybné detekcie. Z týchto výsledkov vyplýva, že jednotlivé deskriptory sú vhodné na rôzne účely, podľa toho, aké textúry máme v úmysle porovnávať.

Literatúra

1. M. Tuceryan a A. K. Jain, „Texture Analysis,“ rev. The Handbook of Pattern Recognition and Computer Vision (2nd Edition), by C. H. Chen, L. F. Pau,, World Scientific Publishing Co., 1998, pp. 207-248.
2. A. Benzaoui, A. Boukrouche a H. Doghmane, „Face recognition using 1DLBP, DWT and SVM,“ rev. 3. International Conference on Control, Engineering and Information Technology (CEIT 2015), Tlemcen, Algeria, 2015.
3. S. Sathiya, M. Balasubramanian a S. Palanivel, „Pattern Recognition Based Detection Recognition of Traffic Sign Using SVM,“ International Journal of Engineering and Technology (IJET), zv. 6, 1. vyd.2, pp. 1147-1157, 2014.
4. O. Kováč, J. Mihalík a P. Čajko, „Obrazové textúry a ich popisovanie,“ Posterus, zv. 9, 1. vyd.3, pp. 1-8, 2016.
5. G. Gimel, „Texture Analysis and Synthesis using a Generic Markov-Gibbs Image Model,“ 2006. [Online]. Available: https://www.cs.auckland.ac.nz/~georgy/research/texture/thesis-html/thesis.html. [Cit. 5 7 2006].
6. R. M. Haralick, K. Shanmugam a I. Dinstein, „Textural features for image classification,“ IEEE Transactions on Systems, Man, and Cybernetics, pp. 610 – 621, 1973.
7. R. Azhar, D. Tuwohigide , D. Kamudi a N. Suciati, „Batik Image Classification Using SIFT Feature Extraction, Bag of Features and Support Vector Machine,“ Procedia Computer Science, zv. 72, pp. 24-30, 2015.
8. M. Kociolek, A. Materka, M. Strzelecki a P. Szczypinski, „Discrete Wavelet Transform – Derived Features for Digital Image Texture Analysis,“ rev. Proc. of International Conference on Signal and Electronic Systems, Lody, 2001.
9. S. Arivazhagan a L. Genesan, „Texture classification using wavelet transform,“ Pattern Recognition Letters, zv. 24, 1. vyd.9-10, p. 1513–1521, 2003.
10. P. Brodatz, Textures: a photographic album for artists and designers, Mineola, New York: DOVER PUBLICATIONS, INC., 1966.
11. O. Kováč, J. Mihalík a P. Čajko, „Algoritmus popisovania obrazových textúr v priestore DWT,“ Posterus, zv. 9, 1. vyd.7, 2016.
12. J. Mihalík a O. Kováč, Číslicové spracovanie textúr ľudskej hlavy, Košice: TU, 2014.

---

Spoluautormi článku sú Ján Mihalík a Patrik Čajko, Laboratórium číslicového spracovania obrazov a videokomunikácií, Katedra elektroniky a multimediálnych telekomunikácií, Fakulta elektrotechniky a informatiky, Technická univerzita v Košiciach.