TESTING AND APPLICATION OF NEW PHENOMENOLOGICAL MATERIAL MODEL FOR FOAM MATERIALS

Testing and Application of New Phenomenological Material Model for Foam Materials

11. Január, 2010, Autor článku: Goga Vladimír, Elektrotechnika, Študentské práce
Ročník 3, číslo 1 Pridať príspevok

New phenomenological material model for solid foam materials is presented. This model describes the uniaxial compression behaviour of foam materials. The phenomenon is the shape of stress-strain curve for compression load case. Stress-strain curves of the specific foam material with different densities could by predicted by using this model.

1 INTRODUCTION

Solid foams (or just the foams) are cellular solids whose microstructure consisting of an interconnected network of struts (open-cells) or plates (closed-cells) (Fig. 1 (Gibson and Ashby, 1997)). The voids which bordered by them thus create cells. These cells are filled by gas or liquid. Natural materials, such as wood, cork and cancellous bone, and man-made materials such as metal honeycombs and polymer and metal foams, are well-known examples of cellular solids.

Fig. 1 Examples of cellular solids:
a) open-cell polyurethane foam,
b) closed-cell polyethylene foam.

Properties of cellular solids depend on the properties of the material that they made from, on their relative density (relative density is ratio $\rho ^* / \rho _S$ , where $\rho ^*$ is the density of the foam and $\rho _S$ that of solid of which the foam is made) and on the cell topology (i.e. cell size, cell shape, open or closed cell morphology, etc.) (Gibson and Ashby, 1997; Tekoglu, 2007). It is possible to make solid foams from polymers, metals, glass and even ceramics. There are many possible applications for cellular materials ranging from light-weight construction, sound and heat insulation, heat exchangers, energy absorption systems, vibration control, acoustical scattering, etc.

1.1 Mechanical properties of foams

Foam behaviour in compression is the most important for the engineering applications. Fig. 2 shows a typical shape of the compression stress-strain curve for foams. The curve exhibits three definite regions: linear elasticity, plateau and densification. At small strains, usually less then 5 %, the behaviour is linear elastic, with a slope equal to the Young modulus of the foam. As the load increases, the foam cells begin to collapse by elastic buckling, plastic yielding or brittle crushing, depending on mechanical properties of the cell walls. Collapse progresses at roughly constant load, giving a stress plateau, until the opposing walls in the cells meet and touch, when densification causes the stress to increase steeply.

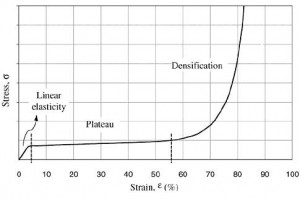
Fig. 2 Typical foam compression stress-strain curve

There have been several models describing the compressive deformation and mechanical properties of cellular materials (Rusch, 1969; Ashby, 1983; Gibson and Ashby, 1988; Gibson and Ashby, 1982), the more recent ones of which are presented by Gibson and Ashby (1988). They predicted that the compressive stress-strain curve of cellular solids, either elastomeric, plastic, or brittle ones, can be divided into mentioned three regions: the linear elastic, the plateau, and the densification. The extent of each region depends on its relative density $( \rho ^* / \rho _S )$ and responds to the different mechanical responses. Gibson and Ashby (1988) in terms of the cubic model of an open and closed-cell cellular material and Euler’s equation built a series of equations to describe the mechanical properties of cellular solids.

For instance: open-cell cellular solid:

linear elastic region:

$\frac{E^*}{E_S} = C_1 \Big ( \frac{\rho ^*}{\rho _S} \Big ) ^2$

(1)

plateau region for plastic foam:

$\frac{\sigma _{pl} ^*}{\sigma _Y} = C_2 \Big ( \frac{\rho ^*}{\rho _S} \Big ) ^{\frac{3}{2}}$

(2)

where $E ^*$ is Young’s modulus of foam, $E _S$ is Young’s modulus of cell wall materials, $\sigma _{pl} ^*$ is plastic collapse stress of plastic foam, $\sigma _Y$ is yielding strength of cell wall material, $\rho ^*$ and $\rho _S$ is density of foam and cell wall material of which the foam is made, respectively, and C₁ and C₂ are constants. Constants C₁ and C₂ were determined from measured data (C₁ = 1 and C₂ = 0,3 gives a good description of a wide range of materials and densities [2], but it is not the rule).

2 NEW PHENOMENOLOGICAL MODEL FOR FOAM MATERIALS

New phenomenological model for foam materials describes the phenomenon, which is in this case the shape of stress-strain curve (Goga and Hučko, 2008). The ambition was to create model with few parameters and every parameter should be depended on relative denity, because mechanical properties like Young’s modulus and plateau stress increases and densification strain (densification strain – it is strain when plateau ends and densification starts) decreases with increasing foam density.

Materials undergoing strain are often modeled with mechanical components, such as springs (restorative force component) and dashpots (damping component). Connecting a spring and damper in series yields a model of a Maxwell material (Fig. 3a.) while connecting a spring and damper in parallel yields a model of a Kelvin-Voight material (Fig. 3b.). These models have been used to modeling the behavior of a viscoelastic materials (creep and stress relaxation). Springs represent the elastic component of a viscoelastic material and dashpots represent the viscous component of a viscoelastic material. Different combinations of these basic models give an opportunity to modeling various behaviors of materials.

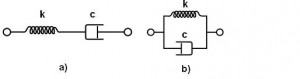
Fig. 3 a) Maxwell model, b) Kelvin-Voight model.

2.1 New foam model

New foam model consists of three systems in parallel (Fig. 4.). The first, referred to as the Maxwell arm, contains a spring (stiffness k) and dashpot (viscosity c) in series. The other two systems contain only springs (k_P and k_D). This model can be used to accurately predict the general shape of the foam’s compressive stress-strain curve.

Fig. 4 Foam model.

Stress-strain response of Maxwell model describes the first and the second region of foam compression deformation, but only if the plateau stress is constant. If the plateau stress increases or decreases, it is necessary to integrate next spring with stiffness k_P parallel with Maxwell model. Stiffness k_P represents a slope of the plateau stress. Densification region is controlled by last spring with nonlinear stiffness kD . This spring is in parallel connection with previous model.

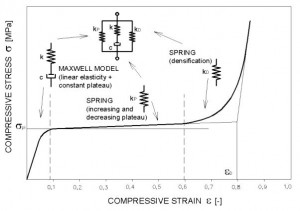
Fig. 5 Stress-strain curve describes by foam model.

Stiffness coefficient k is equivalent to foam Young’s modulus, damping coefficient c is equivalent to plateau stress, stiffness k_P represents a slope of the plateau stress and stiffness coefficient k_D is 2-parameters exponential function of strain (3):

$k_D (\epsilon) = \gamma (1 - e^{\epsilon})^n$

(3)

Finally, the model parameters are: k, c, k_P and $\gamma$ and n from (3).

2.2 Model solving

In order to model this system, the following physical relations must realize:

for series components:

$\sigma_M = \sigma_k = \sigma_c$

(4)

$\epsilon_M = \epsilon_k + \epsilon_c$

(5)

for parallel components:

$\sigma = \sigma_M + \sigma_P + \sigma_D$

(6)

$\epsilon = \epsilon_M = \epsilon_P = \epsilon_D$

(7)

where $\sigma$ and $\epsilon$ is stress and strain of the individual components, respectively.

Definition of stress for the individual components:

$\sigma_k = k \epsilon_k$
$\sigma_c = c \dot{\epsilon} _c$
$\sigma_P = k_P \epsilon_P$	(8)
$\sigma_D = k_D \epsilon_D = \gamma (1 - e ^{\epsilon _D})^n \epsilon _D$

where $\dot{\epsilon} _c$ is strain rate of the dashpot.

For Maxwell model the stress (4), strain (5) and their rates of change with respect to time are governed by equation:

$\dot{\epsilon} _M = \frac{\dot{\sigma} _M}{k} + \frac{\sigma _M}{c}$

(9)

The strain rate is a constant in this foam model (we consider $\dot{\epsilon} _M = 1 s^{-1}$ ). This strain rate is not real rate of compression deformation. This model is not function of strain rate. Than, there is only one derivation element. It is derivation of stress as a function of time. Result of this differential equation is the stress-strain relationship:

$\sigma _M (t) = e^{- \frac{kt}{c}} \Big ( -1 + e^{\frac{kt}{c}} \Big ) c \dot{\epsilon}_M$

(10)

Time t was substituted by strain $\epsilon _M$ :

$t = \frac{\epsilon _M}{\dot{\epsilon _M}}$

(11)

and equation (10) was changed to:

$\sigma _M (\epsilon, \dot{\epsilon _M}) = e^{- \frac{k \epsilon _M}{c \dot{\epsilon}_M}} \Bigg ( -1 + e^{\frac{k \epsilon _M}{c \dot{\epsilon _M}}} \Bigg ) c \dot{\epsilon}_M$

(12)

Strain rate is constant $\dot{\epsilon _M} = 1 s^{-1}$ see above, therefore equation (12) is function only of the strain $\epsilon _M$ :

$\sigma _M (\epsilon _M) = e ^{- \frac{k \epsilon _M}{c}} \Bigg ( -1 +e ^{\frac{k \epsilon _M}{c}} \Bigg ) c$

(13)

With respect to the equations (6 and 7) the finally equation of the foam model is:

$\sigma (\epsilon) = e^{- \frac{k \epsilon}{c}} \Bigg ( - 1 + e^{\frac{k \epsilon}{c}} \Bigg ) c + [k_P + \gamma (1 - e^{\epsilon})^n ] \epsilon$

(15)

Equation (15) presents a stress-strain relationship for modeling stress-strain curve. Influence of model parameters k, c, k_P and parameters $\gamma$ and n on the shape of stress-strain curve is on Fig. 6.

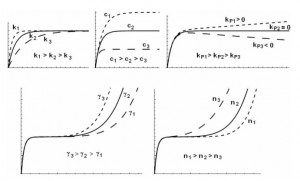
Fig. 6 Influence of model parameters k, c, k_P, $\gamma$ and n.

Function (15) is phenomenological model because it is just a function for modeling the shape of foam materials stress-strain curves.

3 COMPRESSION TEST OF POLYURETHANE FOAM

Uniaxial compression test was performed for open-cell rigid polyurethane (PUR) foam with densities 40, 50, 100 and 145 kg/m³. Testing foam is used as a heat insulation and construction material (foam core sandwich panels).

Mechanical properties were evaluated as a function of foam density using a conventional mechanical test frame (Fig. 7). Tests were conducted at an initial strain rate 0,02 s^-1 and at room temperature. Deformation and acting force was measured by position sensor and compression load cell. For each density was cut one specimen with dimensions 50x50x30 mm. Fig. 8 shows stress-strain ( $\sigma - \epsilon$ ) curves of PUR foams.

Fig. 7 Mechanical test frame.

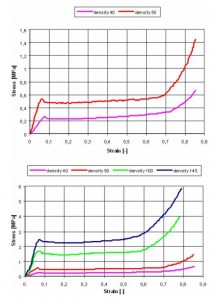
Fig. 8 Compressive stress-strain curves of PUR foams.

Young’s modulus, plastic and plateau stress of measured foams are in Tab. 1.

Tab. 1 Mechanical properties of measured foams.

foam density [kg/m³]	Young’s modulus [MPa]	plastic stress [MPa]	plateau stress [MPa]
40	3,7	0,26	0,23
50	9,8	0,54	0,47
100	26,4	1,67	1,46
145	37,3	2,45	2,24

4 MODEL APPLICATIONS

Four foam specimens with different densities were compressed. Their stress-strain curves were approximated by new foam model. Least square method was used to find a good estimation of model parameters. Calculated parameters are in Tab. 2. Modeled and measured curves are compared in Fig. 9.

Tab 2. Model parameters.

foam density [kg/m³]	k [MPa]	c [MPa]	k_P [MPa]	γ [MPa]	n [-]
40	6,817	0,222	0,085	0,073	6
50	16,46	0,465	0,085	0,176	6
100	45,68	1,481	0,09	1,181	6
145	60,485	2,25	0,1	2,25	4

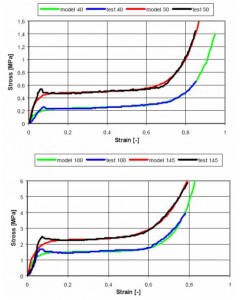
Fig. 9 Modelled and measured stress-strain curves.

Comparison is specific energy, what is the work done per unit volume (16) in deforming the foam to a given strain $\epsilon$ is simply the area under the stress-strain curve.

$W = \displaystyle \int ^{\epsilon} _0 \sigma (\epsilon) d \epsilon$

(16)

Polynomial equation of the 8^th degree was used to calculate specific energies. Those results were compared with energies calculated from new foam model in Tab. 3.

Tab. 3 Specific energies.

density [kg/ m³]	40		50		100		145
Energy W [MJ/m³]	polyn.	model	polyn.	model	polyn.	model	polyn.	model
$\epsilon$ = 20%	0,039	0,039	0,085	0,082	0,254	0,25	0,382	0,369
$\Delta$ W [%]	0		-3,5		-1,6		-3,4
$\epsilon$ = 40%	0,087	0,088	0,182	0,18	0,549	0,552	0,836	0,827
$\Delta$ W [%]	1,2		-1,1		0,6		-1,1
$\epsilon$ = 60%	0,145	0,142	0,286	0,283	0,856	0,87	1,337	1,336
$\Delta$ W [%]	-2,17		-1,1		1,6		-0,1
$\epsilon$ = 80%	0,228	0,213	0,436	0,426	1,352	1,411	2,171	2,177
$\Delta$ W [%]	-6,6		-3		4,4		0,28

5 ESTIMATION OF STRESS-STRAIN CURVE

Stress-strain curve for PUR foam with density 60 kg/m³ was firstly modelled and then compared with measured data.

Fig. 10 shows the relationships of the model parameters on relative density except the parameter n. This parameter must be even and its values are numbers 4 or 6. Solid density 1200 kg/m³ was used to calculate relative density (Ashby, 1983; Goods et al., 1998; Roff and Scott 1971).

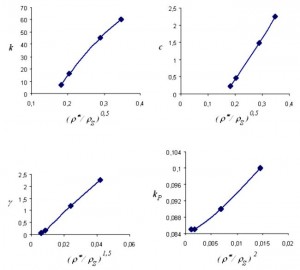
Fig. 10 Model parameters vs. relative density.

Linear approximations of model parameters:

$\displaystyle k = 325,62 \Big ( \frac{\rho ^*}{\rho _S} \Big )^{0.5} - 50,915$
$\displaystyle c = 12,268 \Big ( \frac{\rho ^*}{\rho _S} \Big )^{0,5} - 2,0331$	(17)
$\displaystyle k_P = 1,1271 \Big ( \frac{\rho ^*}{\rho _S} \Big )^{2} + 0,0831$
$\displaystyle \gamma = 61,316 \Big ( \frac{\rho ^*}{\rho _S} \Big )^{1,5} - 0,3163$

Calculated parameters (17) for PUR foam with density 60 kg/m³:

k = 21,9 MPa, c = 0,71 MPa, k_P = 0,086 MPa, $\gamma$ = 0,369 MPa and n = 6.

Modelled stress-strain curve for PUR foam with density 60 kg/m³ was compared with measured curve in Fig. 11. Comparison of the specific energies for this foam is in Tab. 4. Differences of calculated energies ( $\Delta$ W) are less than 10 %.

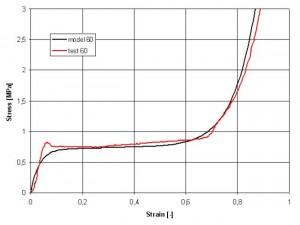
Fig. 11 Foam (60 kg/m³) modelled and measured stress-strain curves.

Tab. 4 Specific energy – foam with density 60 kg/m³.

density [kg/ m³]	60
Energy W [MJ/m³]	polynomial	model
$\epsilon$ = 20%	0,131	0,121
$\Delta$ W [%]	-7,6
$\epsilon$ = 40%	0,281	0,268
$\Delta$ W [%]	-4,6
$\epsilon$ = 60%	0,435	0,423
$\Delta$ W [%]	-2,8
$\epsilon$ = 60%	0,609	0,649
$\Delta$ W [%]	6,6

6 CONCLUSION

New phenomenological foam model was presented. This model was used for approximation measured stress-strain curves from uniaxial compression test of four PUR foam specimens with different densities. Model parameters for each density were obtained. Relationships between parameters and relative density of foam were created and they were used for modelling the stress-strain curve of the same foam with density, which was not be compressed firstly.

Specific energies were calculated for measured curves. The curves were approximated with polynomial and foam model equation. These energies were compared. For all foam specimens differences of the calculated energies were less than 10 %.

New foam model is useful for prediction the shape of stress-strain curves (mechanical properties) of foam materials in compression. It is necessary to making the approximation of model parameters for certain foam material. Model parameters depend on foam’s relative density. It doesn’t consider a temperature, compression strain rate or cell topology of the foam.

AKCNOWLEDGEMENT

This article has been accomplished under VEGA grant no. 1/4122/07.

REFERENCES

Ashby, M.F. (1983). Metall. Trans. A, vol. 14A, p. 1755- 69.
Gibson, L.J. and M.F. Ashby (1982). Proc. R. Soc. London, vol. A382, p. 43.
Gibson, L.J. and M.F. Ashby (1988). Cellular Solids: Structure and Properties, Pergamon Press, Oxford, United Kingdom.
Gibson, L.J. and M.F. Ashby (1997). Cellular solids: structure and properties. 2^nd edition, Cambridge, University Press, Cambridge.
Goga, V and B. Hučko (2008). Compression stress-strain curve modeling of cellular solids. XII. International Conference on Mechanical Engineering.
Goods, S.H., C.L. Neuschwanger, C.C. Henderson and D.M. Skala (1998). Mechanical Properties of CRETE, a Poluyrethane Foam, Journal of Applied Polymer Science, vol. 68, p. 1045.
Roff, W.F. and J.R. Scott (1971). Fibres, Films, Plastics and Rubbers – A Handbook of Common Polymers, Butterworths, London.
Rusch, K.C. (1969). J. Appl. Polym., vol. 13, p. 2297.
Tekoglu, C. (2007). Size effects in cellular solids. PhD Thesis, Rijksuniveriteit Groningen Institute for Metals Research.

2 príspevky(ov) k článku “Testing and Application of New Phenomenological Material Model for Foam Materials”

Sudhanshu napísal:
13. September, 2010 o 15:07
Hi
I found your article very interesting. But I was not able to look at the equations. Can you be so kind to provide a pdf version of this document.
Regards
Sudhanshu
Dr. Molinas napísal:
29. September, 2011 o 19:19
I would be pleased if you can send me a PDF copy of the aricle on Phenomenological Material Model for Foam

O časopise

Meta

RSS

Testing and Application of New Phenomenological Material Model for Foam Materials

2 príspevky(ov) k článku “Testing and Application of New Phenomenological Material Model for Foam Materials”

Napísať príspevok

Rubriky

Burza práce

Štúdijné materiály

Archív