Minulé časti seriálu boli venované tvorbe grafov v Matlabe. Doposiaľ sme si ale vysvetlili iba grafy dvojrozmerné. Dnešná časť poodhalí tému 3D grafov. Pôjde o vizualizáciu funkcií dvoch premenných. Ukážeme, že aj v tejto oblasti je Matlab vysoko fundovaný a pri využití handles sú obmedzenia minimálne.

Samotná podstata 3D grafu vychádza zo zobrazenia priebehu funkcie, kde máme dve premenné nezávislé a jednu závislú. Práve funkčné hodnoty závislej premennej vychádzajú z hodnôt premenných nezávislých. Matematicky sa zvykne takáto závislosť zapisovať ako :

z=f(x,y)

V tomto prípade sú nezávislé premenné x a y. Premenná z je premennou závislou od premenných x a y. Do grafov sa obvykle vykresluje závislosť v karteziánskom súradnicovom systéme. Ide teda o sústavu vzájomne kolmých osí. Zatiaľčo v 2D grafoch tvorí závislosť čiaru, v 3D grafoch je výsledkom plocha. Skutočnosť je logickým dôsledkom toho, že definičný obor funkcie jednej premennej môžeme zakresliť ako úsečku, resp. priamku. V prípade 3D grafu je definičným oborom rovina, alebo presne definovaná plocha. Preto ak sme v Matlabe kreslili graf jednej premennej, postačovalo nám na definovanie nezávislej premennej vytvoriť vektor. Pre tvorbu 3D grafov potrebujeme ale definovať plochu. Práve za týmto účelom bol vytvorený príkaz meshgrid. Príkaz vytvorí dve matice, ktoré budú navzájom kolmé. Spoločne sú predurčené na výpočet funkčných hodnôt závislej premennej.

Predpokladajme, že chceme vytvoriť definičný obor na intervale <-1 ; 1> pre súradnicu X aj Y. Nech je tento obor tvorený mriežkou s krokom 0,5. Použijeme príkaz meshgrid.

>> [X,Y]=meshgrid(-1:0.5:1,-1:0.5:1)
X =
-1.0000 -0.5000 0 0.5000 1.0000
-1.0000 -0.5000 0 0.5000 1.0000
-1.0000 -0.5000 0 0.5000 1.0000
-1.0000 -0.5000 0 0.5000 1.0000
-1.0000 -0.5000 0 0.5000 1.0000

Y =
-1.0000 -1.0000 -1.0000 -1.0000 -1.0000
-0.5000 -0.5000 -0.5000 -0.5000 -0.5000
0 0 0 0 0
0.5000 0.5000 0.5000 0.5000 0.5000
1.0000 1.0000 1.0000 1.0000 1.0000


Matice X a Y tvoria definičný obor v zmysle požiadaviek. Matice sú teraz vo vhodnom formáte, takže na tomto obore môžeme vypočítať funkčné hodnoty závislej premennej funkcie. Ako príklad zvoľme jednoduchú kvadratickú funkciu definovanú vzťahom

Z=X² + Y²

Výsledkom tejto funkcie by mala byť matica Z. Jej jednotlivé prvky sú závislé od hodnôt a súradníc matíc X a Y. Je zrejmé, že matica Z bude mať rovnaký rozmer ako matice X a Y. Jednotlivé bunky matice Z budeme počítať takto :

>> Z(1,1)=X(1,1)^2+Y(1,1)^2
Z =
2

>> Z(1,2)=X(1,2)^2+Y(1,2)^2
Z =
2.0000 1.2500

>> Z(1,3)=X(1,3)^2+Y(1,3)^2
Z =
2.0000 1.2500 1.0000

>> Z(1,4)=X(1,4)^2+Y(1,4)^2
Z =
2.0000 1.2500 1.0000 1.2500

>> Z(1,5)=X(1,5)^2+Y(1,5)^2
Z =
2.0000 1.2500 1.0000 1.2500 2.0000

>> Z(2,1)=X(2,1)^2+Y(2,1)^2
Z =
2.0000 1.2500 1.0000 1.2500 2.0000
1.2500 0 0 0 0

Vidíme, že sa nám postupne matica Z plní funkčnými hodnotami. Každému je ale zrejmé, že takýto postup by bol značne zdĺhavý. Programátora by isto napadlo celú opakujúcu sa výpočtovú sekvenciu vložiť do dvojice vnorených cyklov a postupne vypočítať všetky funkčné hodnoty funkcie. Potešilo by nás aj to, že matice X a Y sú logicky usporiadané a práca s ich indexami je úplne jednoduchá. Sila Matlabu ale tkvie v tom, že aj zložito vyzerajúce úlohy sa dajú riešiť jednoducho. Ak si vzpomenieme na základné matematické operácie v Matlabe, tak zistíme, že sa dajú použiť aj efektívne zápisy, ktoré spracúvajú celé vektory alebo matice po prvkoch. Reč je o symbole bodka, ktorá sa zapisuje pred danú matematickú operáciu. Preto úlohu výpočtu funkčných hodnôt Z nebudeme riešiť ani krvopotným opakovaním príkazov na výpočet každej hodnoty zvlášť a nebudeme ani programovať vnorené cykly. Využijeme práve operátor bodka. Zápis bude vyzerať takto :

>> Z=X.^2+Y.^2
Z =
2.0000 1.2500 1.0000 1.2500 2.0000
1.2500 0.5000 0.2500 0.5000 1.2500
1.0000 0.2500 0 0.2500 1.0000
1.2500 0.5000 0.2500 0.5000 1.2500
2.0000 1.2500 1.0000 1.2500 2.0000

Vidíme, že pomocou jednoriadkového príkazu sme sa dopracovali k požadovanému výsledku. Je to aj vďaka vhodne vytvoreným maticiam X a Y pomocou príkazu meshgrid.

Teraz už vieme postup generovania definičného oboru ako aj výpočet funkčných hodnôt. Môžeme teda pristúpiť k samotnému zobrazovaniu do grafu. Uvedená definícia a výpočet matíc X, Y a Z je však nevhodná. Definovaná mriežka je pomerne hrubá a graf by vyzeral „hranato“. Preto si nanovo definujeme všetky matice. Nech je krok v mriežke definičného oboru 0,1. Funkčnú závislosť necháme bez zmeny.

>> [X,Y]=meshgrid(-1:0.1:1,-1:0.1:1);
>> Z=X.^2+Y.^2;

Na takto definovanej funkcii si demonštrujme základné príkazy na tvorbu 3D grafov. Jedná sa o rôzne typy zobrazenie tej istej závislosti.

• mesh
• surf
• contour

Použitie príkazov je podobné. Ako prvé dva parametre slúžia matice definujúce oblasť na ktorej sa má graf vykresliť. Tretím parametrom sú funkčné hodnoty funkcie. V našom prípade bude zápis takýto :

>> mesh(X,Y,Z)

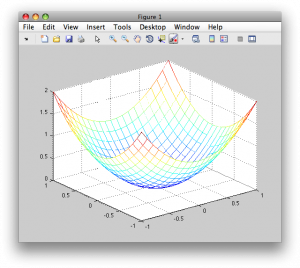
Obr. 1. Výsledok zobrazenie pomocou príkazu mesh

Analogicky môžeme použiť aj ostatné dva príkazy.

>> surf(X,Y,Z)

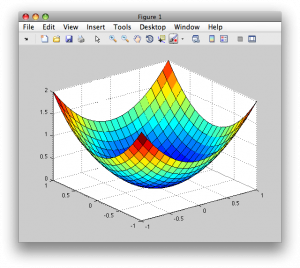
Obr. 2. 3D graf vytvorený príkazom surf

>> contour(X,Y,Z)

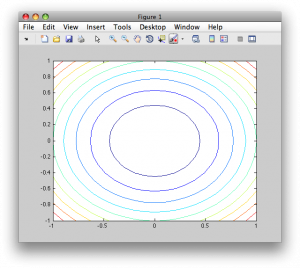
Obr. 3. Vrstevnicový graf – príkaz contour

Rovnako ako v 2D grafoch je možné použiť príkazy na popis osí aj v 3D grafe.

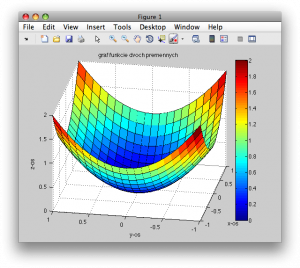
>> surf(X,Y,Z)
>> xlabel('x-os')
>> ylabel('y-os')
>> zlabel('z-os')
>> title('graf funkcie dvoch premennych')

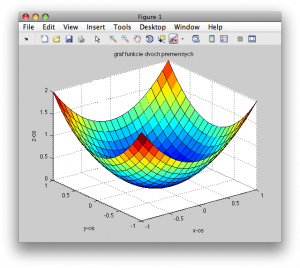
Obr. 4. 3D graf s popisom osí a nadpisom

Lepšiu predstavu o veľkosti funkčnej hodnoty navodí použitie farebnej stupnice – colorbar.

>> colorbar

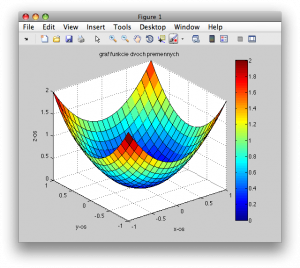
Obr. 5. Farebná stupnica – colorbar

Vypnúť colorbar je možné príkazom colorbar off.

Grafom sa dá aj otáčať. Efekt dosiahneme viacerými spôsobmi. Najjednoduchší je využiť interaktívnu obsluhu grafu a stlačiť ikonu Rotate 3D. Pomocou myši meníme elevačný uhol a azimut. Oba tieto parametre sa dajú meniť aj príkazom view. Ako prvý do funkcie vstupuje azimut a druhý je elevačný uhol. Oba sa udávajú v stupňoch.

>> view([-80 30])

Obr. 6. Natočenie 3D grafu

Rovnakého efektu dosiahneme ak použijeme jednu z vlastností grafu. Najskôr musíme získať handler na osi grafu (príkaz gca).

>> a=gca;

Jednou z vlastností je View a má rovnaký význam ako príkaz view. Aktuálnu hodnotu natočenia teda získame príkazom.

>> get(a,'View')
ans =
-80 30

Na zmenu natočenia využijeme príkaz set.

>> set(a,'View',[-30 50])

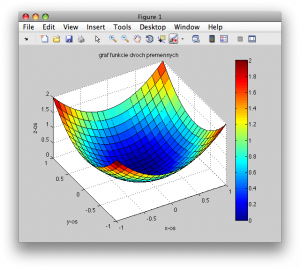
Obr. 7. Natočenie grafu pomocou vlastnosti objektu

Uviedli sme si ako kresliť funkčné závislosti s výslednou 3D plochou. Matlab ale dovoľuje kreslenie aj spojnicových grafov v 3D. Slúži na to príkaz plot3. Jeho použitie je obdobné ako klasický plot. Rozdielom je, že neudávame usporiadanú dvojicu bodov, ale usporiadanú trojicu. Tieto trojice sú zadané ako samostatné vektory. Príkaz plot3 pospája definované body v priestore. Ako príklad nám poslúži kód uvedený v helpe k tomuto príkazu. Jedná sa o zobrazenie závitnice.

>> t = 0:pi/50:10*pi;
>> plot3(sin(t),cos(t),t);
>> grid

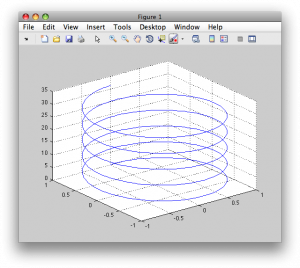
Obr. 8. 3D závitnica pomocou príkazu plot3

Do oblasti vykreslovanie 3D obrázkov by sme mohli zahrnúť aj príkaz patch, ktorý sa využíva pri tvorbe ako 2D tak 3D grafických objektov. Ide ale skôr o definície objektov ako kocka, hramol, alebo ihlan. Tejto téme sa budeme venovať v niektorom z ďalších pokračovaní seriálu. Špeciálnym nástrojom pre prácu s 3D objektami je Simulink 3D Animation (v minulosti označovaný ako Virtual Reality Toolbox). Tento produkt si ale vyžaduje vedomosti z oblasti VRML ako aj znalosť Simulinku. V budúcnosti tomuto zaujímavému produktu budeme venovať niekoľko dielov seriálu.

Literatúra

1. Matlab 7 – Graphics, The MathWorks,
   http://www.mathworks.com/access/helpdesk/help/pdf_doc/matlab/graphg.pdf, 24.9.2009