Matlab - Základné matematické funkcie

22. Matlab – Základné matematické funkcie

05. Marec, 2010, Autor článku: Blaho Michal, MATLAB/Comsol
Ročník 3, číslo 3 Pridať príspevok

V dnešnej časti si povieme niečo o základných matematických funkciách. Ich využitie je veľké v každej oblasti, ktorá využíva matematiku. Matlab ich samozrejme podporuje v mnoho funkciách. Dnešná časť bude teda venovaná trigonometrickým, exponenciálnym, logaritmickým a mocninovým funkciám. V závere si ešte ukážeme ako môžeme v Matlabe zaokrúhľovať, celočíselne deliť a získavať zvyšok po delení.

Trigonometrické funkcie

Trigonometrické funkcie sú funkcie, ktoré vyjadrujú vzťahy medzi uhlom a dĺžkami strán v trojuholníku (väčšinou pravouhlom obr.1)

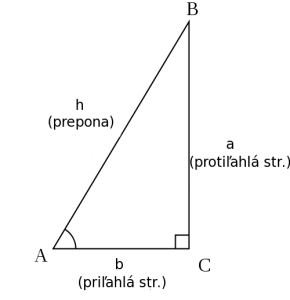
Obr. 1 Pravouhlý trojuholník (prevzaté z [1])

Trigonometrické funkcie sa dajú definovať aj na jednotkovej kružnici ako je to na obr.2.

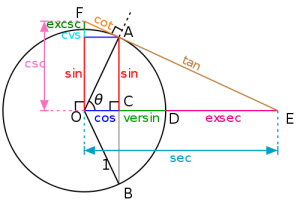
Obr. 2 Trigonometrické funkcie na jednotkovej kružnici (prevzaté z [1])

Matlab obsahuje funkcie na výpočet trigonometrických funkcií, ktoré dokážu pracovať s argumentami v stupňoch aj radiánoch. Napriek tomu ešte uvedieme prepočet medzi týmito dvomi jednotkami.

$stup = rad \frac{180}{\pi}$ ; $rad = stup \frac{\pi}{180}$

(1)

Sínus

Sínus uhla v pravouhlom trojuholníku (obr.1) pri vrchole A je definovaný ako pomer protiľahlej strany ku prepone

$sin(\alpha)=\frac{a}{h}$

(2)

Matlab obsahuje nasledovné funkcie na výpočet sínusu

Tab. 1 Funkcie na výpočet sínusov v Matlabe

Príkaz	Popis
sin	Sínus (argument v radiánoch)
sind	Sínus (argument v stupňoch)
sinh	Hyperbolický sínus
asin	Arcussínus (výsledok v radiánoch)
asind	Arcussínus (výsledok v stupňoch)
asinh	Hyperbolický arcussínus

Kosínus

Kosínus uhla v pravouhlom trojuholníku (obr.1) pri vrchole A je definovaný ako pomer priľahlej strany ku prepone

$cos(\alpha)=\frac{b}{h}$

(3)

Výpočet kosínusu sa dá v Matlabe realizovať funkciami

Tab. 2 Funkcie na výpočet kosínusov v Matlabe

Príkaz	Popis
cos	Kosínus (argument v radiánoch)
cosd	Kosínus (argument v stupňoch)
cosh	Hyperbolický kosínusus
acos	Arcuskosínus (výsledok v radiánoch)
acosd	Arcuskosínus (výsledok v stupňoch)
acosh	Hyperbolický arcuskosínus

Tangens

Tangens uhla v pravouhlom trojuholníku (obr.1) pri vrchole A je definovaný ako pomer protiľahlej strany ku priľahlej strane

$tan(\alpha)=\frac{a}{b}$

(4)

Matlab obsahuje nasledovné funkcie na výpočet tangensu

Tab. 3 Funkcie na výpočet tangensov v Matlabe

Príkaz	Popis
tan	Tangens (argument v radiánoch)
tand	Tangens (argument v stupňoch)
tanh	Hyperbolický tangens
atan	Arcustangens (výsledok v radiánoch)
atand	Arcustangens (výsledok v stupňoch)
atanh	Hyperbolický arcustangens

Kotangens

Kotangens uhla v pravouhlom trojuholníku (obr.1) pri vrchole A je definovaný ako pomer priľahlej strany ku protiľahlej strane

$cot(\alpha)=\frac{b}{a}$

(5)

Matlab obsahuje nasledovné funkcie na výpočet kotangensu

Tab. 4 Funkcie na výpočet sínusov v Matlabe

Príkaz	Popis
cot	Kotangens (argument v radiánoch)
cotd	Kotangens (argument v stupňoch)
coth	Hyperbolický kotangens
acot	Arcuskotangens (výsledok v radiánoch)
acotd	Arcuskotangens (výsledok v stupňoch)
acoth	Hyperbolický arcuskotangens

Sekans

Sekans uhla v pravouhlom trojuholníku (obr.1) pri vrchole A je definovaný ako inverzná hodnota kosínusu. Je to pomer prepony ku priľahlej strane

$sec(\alpha)=\frac{h}{b}=\frac{1}{cos(\alpha)}$

(6)

Sekans môžeme v Matlabe vypočítať nasledujúcimi funkciami

Tab. 5 Funkcie na výpočet sekansov v Matlabe

Príkaz	Popis
sec	Sekans (argument v radiánoch)
secd	Sekans (argument v stupňoch)
sech	Hyperbolický sekans
asec	Arcussekans (výsledok v radiánoch)
asecd	Arcussekans (výsledok v stupňoch)
asech	Hyperbolický arcussekans

Kosekans

Kosekans uhla v pravouhlom trojuholníku (obr.1) pri vrchole A je definovaný ako inverzná hodnota kosínusu. Je to pomer prepony ku priľahlej strane

$csc(\alpha)=\frac{h}{a}=\frac{1}{sin(\alpha)}$

(7)

Kosekans môžeme v Matlabe vypočítať nasledujúcimi funkciami

Tab. 6 Funkcie na výpočet kosekansov v Matlabe

Príkaz	Popis
csc	Kosekans (argument v radiánoch)
cscd	Kosekans (argument v stupňoch)
csch	Hyperbolický kosekans
acsc	Arcuskosekans (výsledok v radiánoch)
acscd	Arcuskosekans (výsledok v stupňoch)
acsch	Hyperbolický arcuskosekans

Vypočet niekoľkých hodnôt trigonometrických funkcií si uvedieme v nasledujúcich príkladoch

>> sin(pi/4) ans = 0.7071 >> acosd(0.5) ans = 60.0000 >> tan(pi/4) ans = 1.0000 >> cscd(30) ans = 2.0000

Exponenciálne funkcie

Funkcie

$y=e^x$

(8)

kde e je približne 2.7183 nazývame exponenciálne funkcie. Exponenciálna funkcia sa zvykne ešte vyjadrovať pomocou nasledovného Taylorovho radu

$e^x=\sum_{n=0}^{\inf} \frac{x^n}{n!} = 1+x+\frac{x^2}{2!} + \frac{x^3}{3!} + ..$

(9)

pre prácu s komplexnými číslami platí nasledujúci vzťah

$e^{x+yi}=e^x (cos(y)+i.sin(y))$

(10)

Príkazy pre prácu s exponenciálnymi funkciami nájdete v ďalšej tabuľke

Tab. 7 Funkcie na výpočet exponenciálnych funkcií v Matlabe

Príkaz	Popis
exp	Exponenciál
expm	Maticový exponenciál
expm1	Výpočet exp(x)-1 presne pre malé x

Hodnotu čísla e teda vieme v Matlabe zistiť ako jeho prvú mocninu. Funkcia expm1 sa využíva na presný výpočet malých hodnôt x, kde dochádza ku zaokrúhľovaniu.

>> format long >> exp(1) ans = 2.718281828459046

Logaritmické funkcie

Logaritmus čísla x je číslo, ktorým by sme museli umocniť základ b, aby sme dostali číslo x teda ak

$x=b^y$

(11)

potom

$y=log_{b}(x)$

(12)

v Matlabe môžete využiť nasledujúce funkcie

Tab. 8 Funkcie na výpočet logaritmických funkcií v Matlabe

Príkaz	Popis
log	Prirodzený logaritmus
log10	Dekadický logaritmus
log1p	Výpočet log(x)-1 presne pre malé x
log2	Logaritmus so základom 2, prípadne rozdelenie čísla na exponent a mantisu
reallog	Prirodzený logaritmus nezáporných matíc

Prirodzený základ má bázu rovnú číslu e, dekadický číslu 10. V užívateľskej príručke nájdete zaujímavý výpočet známeho čísla, ktorý je uvedený aj v príklade

>> abs(log(-1))

Mocniny a odmocniny

Ako spraviť mocninu ste sa už dočítali v skorších častiach nášho seriálu. Matlab obsahuje ďalšie užitočné funkcie pre prácu s mocninami a odmocninami

Tab. 9 Funkcie na výpočet mocnín a odmocnín v Matlabe

Príkaz	Popis
nextpow2	Najbližšia vyššia mocnina čísla 2
nthroot	N-tá odmocnina reálnych čísel
pow2	Vektor mocnín 2 na vstupný argument
realpow	Mocnina prvkov matice X prvkami matice Y
realsqrt	Odmocnina nezáporných matíc
sqrt	Druhá odmocnina

Využitie niektorých funkcií nájdete v nasledujúcich príkladoch

>> nextpow2(30) ans = 5 >> realpow([2 5 7],[2 3 2]) ans = [4 125 49]

Zaokrúhľovanie

Ako každé výpočtové prostredie aj Matlab obsahuje funkcie na zaokrúhľovanie čísiel. Čísla vieme zaokrúhliť v niekoľkých smeroch ku celému číslu. Funkcie na zaokrúhľovanie sú popísané v nasledujúcej tabuľke.

Tab. 10 Funkcie na zaokrúhľovanie v Matlabe

Príkaz	Popis
ceil	Zaokrúhlenie smerom ku kladnému nekonečnu
fix	Zaokrúhlenie smerom ku nule
floor	Zaokrúhlenie smerom ku zápornému nekonečnu
round	Zaokrúhlenie ku najbližšiemu celému číslu

Fungovanie funkcií si ukážeme aj na nasledovnom príklade

>> cisla = [-2.79 2.25]; >> ceil(cisla) ans = [-2 3] >> fix(cisla) ans = [-2 2] >> floor(cisla) ans = [-3 2] >> round(cisla) ans = [-3 2]

Celočíselné delenie

Niekedy je potrebné vyjadriť výsledok podielu ako celé číslo prípadne nás zaujíma čo nám po delení zostane ako zvyšok. Nasledujúce funkcie nám tieto operácie uľahčujú

Tab. 11 Funkcie na celočíselné delenie a zvyšky po delení v Matlabe

Príkaz	Popis
idivide	Celočíselné delenie so zaokrúhlením
mod	Modulus delenia
rem	Zvyšok delenia

Príkaz idivide delí dve celé čísla pričom výsledok je zaokrúhlený. Zaokrúhľovanie sa vykonáva jednou z vyššie spomenutých zaokrúhľovacích funkcií, ktoré sa zadávajú ako tretí argument funkcie. Príkazy mod a rem vracajú hodnoty výrazu X-n.*Y s rozdielom, že pri príkaze mod je n=floor(X./Y) a pri príkaze rem je n=fix(X./Y), čo sa prejaví hlavne ak maju X a Y rozdielne znamienka ako je to vidno na príklade

>> x=int32(-10) >> y=int32(3) >> idivide(x,y,'floor') ans = -4 >> mod(x,y) ans = 2 >> rem(x,y) ans = -1

Literatúra

1 príspevok k článku “22. Matlab – Základné matematické funkcie”

Matúš napísal:
03. Júl, 2010 o 14:37
Matlab je skvelý program,ktorý by som každému kto má záujem či už o matematiku či fyziku .

O časopise

Meta

RSS

22. Matlab – Základné matematické funkcie

1 príspevok k článku “22. Matlab – Základné matematické funkcie”

Napísať príspevok

Rubriky

Burza práce

Štúdijné materiály

Archív