Heuristický adaptívny PSD regulátor založený na miere kmitavosti
28. Apríl, 2010, Autor článku: Šlezárová Alexandra, Elektrotechnika
Ročník 3, číslo 4  Pridať príspevok
Pridať príspevok
 Článok spočíva v predstavení a opísaní algoritmu adaptívného riadenia, ktorý patrí do skupiny heuristických adaptívnych riadení. Ďalej sa snaží objasniť a vysvetliť metódy a postupy pri správe riadenia a zabezpečenia stability riadiacich systémov, poprípade ako postupovať pri problémoch so stabilitou. Článok opisuje zákony a podmienky, ktoré treba splniť a taktiež základný algoritmus na základe, ktorého sme dosiahli čo najideálnejšie výsledky.
Článok spočíva v predstavení a opísaní algoritmu adaptívného riadenia, ktorý patrí do skupiny heuristických adaptívnych riadení. Ďalej sa snaží objasniť a vysvetliť metódy a postupy pri správe riadenia a zabezpečenia stability riadiacich systémov, poprípade ako postupovať pri problémoch so stabilitou. Článok opisuje zákony a podmienky, ktoré treba splniť a taktiež základný algoritmus na základe, ktorého sme dosiahli čo najideálnejšie výsledky.
Úvod
Adaptívne riadenie ako celok je dôležitou a neodmysliteľnou súčasťou a aj diskutabilnou témou a problematikou vo viacerých odvetviach priemyslu. Taktiež je skúmaným smerom v Teórii automatického riadenia. Najčastejšie sa adaptívne riadenie využíva hlavne v leteckom, automobilovom a kozmonautickom odvetví. Adaptívne riadenie potrebuje veľa času na proces adaptácie, kde sa menia spôsoby riadenia, tak aby riadený systém vhodne reagoval na zmenené podmienky. Heuristické regulátory využívajú klasické (PID – spojité a PSD – diskrétne) regulátory. Najznámejší heuristický algoritmus je Maršíkov algoritmus, kde pozorujeme hlavne mieru kmitavosti kappa – . Uvedený je aj postup výpočtu Maršíkovho algoritmu.
1. Heuristický adaptívny PSD regulátor založený na miere kmitavosti
Maršíkov prístup je postavený na skúsenosti, že ozvy optimálne nastavených regulačných obvodov sa vyznačujú podobným tvarom s maximálne jedným prekmitom. Adaptácia je zameraná na zabezpečovanie stanoveného tvaru ozvy regulačnej odchýlky udržiavaná konštantnej hodnote kritéria kvality v podobe miery kmitavosti regulačnej odchýlky. [1]
1.1 Miera kmitavosti
Miera kmitavosti je definovaná bezrozmerným indexom , ktorý udáva pomer frekvencie prechodov nulou regulačnej odchýlky e a jej prvej derivácie
| (1) |
kde fe je frekvencia prechodu nulou e a fv je frekvencia prechodu nulou jej prvej derivácie. Čím je regulačný proces tlmenejší, tým je menšia hodnota indexu , potom platí:
| (2) |
Na výpočet miery kmitavosti je nevyhnutná dobrá filtrácia vysokofrekvenčných šumov, ktorých pôsobenie zapríčiňuje chybnú hodnotu indexu kmitavosti. Ozvy optimálne nastavených regulačných obvodov sa často vyznačujú jedným nevýrazným prekmitom, index kmitavosti majú . Hlavnou požiadavkou je udržiavať index kmitavosti na stanovenej hodnote. Je zrejmé, že s narastajúcim zosilnením K index kmitavosti
rastie. Ak by platila lineárna charakteristika
| (3) |
kde Kc je kritická hodnota zosilnenia regulátora na hranici stability, v jednom kroku by sme mohli nastaviť parametre regulátora tak, aby sa dosiahla želaná odozva. Zákon adaptácie musí byť taký, aby sa index kmitavosti udržiaval na želanej hodnote , kde pre zmenu celkového zosilnenia platí:
| (4) |
kde je zosilnenie adaptácie, avšak Maršík odporúča zákon adaptácie [1] :
| (5) |
1.2 Podmienky na aplikáciu algoritmu
- regulovanú sústavu musíme mať stabilnú, s veľmi malou kmitavou prechodovou charakteristikou s ľubovoľným rádom a malým dopravným oneskorením,
- vyhodnocujeme iba skutočné regulačné odozvy bez parazitných šumov. Vysokofrekvenčné šumy, na ktoré má regulačná odchýlka problém reagovať musia byť odfiltrované, aby neskresľovali výpočet
. Na nevýrazné šumy stačí 10 vzoriek na celú prechodovú charakteristiku. Veľmi účinná je filtrácia kĺzavými priemermi alebo použitím nelineárneho filtra. Vysokofrekvenčné šumy veľmi zle ovplyvňujú index kmitavosti ,
teda jeho výpočet, prejavia sa tým, že ho znižujú, čo zvyšuje zložku
a to znamená kmitavejšiu odozvu,
- ak regulácia prebieha so skokmi žiadanej hodnoty W mal by sa zaradiť adaptívny jednokapacitný filter pre žiadanú hodnotu s časovou konštantou:
| (6) |
kde w(n) je zadaná hodnota a wfilt je filtrovaná žiadaná hodnota. Počiatočné podmienky na výpočet stredných hodnôt kvadrátov regulačnej odchýlky a ich diferencií je najvhodnejšie zvoliť, pretože je potrebné zabrániť deleniu nulou v prvých krokoch algoritmu [2]:
| (7) |
2. Postup výpočtu adaptívneho PSD algoritmu podľa Maršíka
- výpočet regulačnej odchýlky e(n) z y(n) a filtrovanej žiadanej hodnoty wfilt:
- analýza veľkosti regulačnej odchýlky a zistenie, či je vôbec nutné adaptovať, ak je splnená podmienka
- vypočítame rozptyl regulačnej odchýlky
s pomalým zabúdaním
- vypočítame stredné hodnoty kvadrátov odchýlok a ich diferencie s rýchlym zabúdaním
- filtrovanie žiadanej hodnoty Wfilt zo skutočnej žiadanej hodnoty W:
- určíme index kmitavosti
- adaptácia spoločného zosilnenia regulátora
- vyrátame koeficient proporcionálnej zložky regulátora
- vyrátame koeficient diferenčnej zložky regulátora
- výpočet akčnej veličiny regulátora
- skok na krok číslo 1 [3]
3. Výsledky simulácií
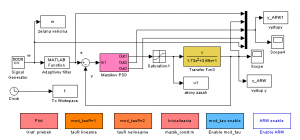
Na základe uvedeného algoritmu, sme zostrojili schému (obr. 1), ktorá nám bude prinášať nasledujúce výsledky simulácie. Prenosovú funkciu sme zvolili druhého rádu[4]
Počiatočné nastavovacie konštanty sme volili veľmi malé. Počiatočné hodnoty stále zostávajú rovnaké. Tieto počiatočné konštanty sa nastavujú podľa rádu zvolenej prenosovej funkcie. Hodnoty, ktoré môžeme meniť a od, ktorých závisí adaptácia a jej výsledok sú miera kmitavosti kappa – , rýchlosť
adaptácie – a perióda vzorkovania Ts=0.01. Ďalej sme taktiež skúšali meniť periódu vzorkovania a aj rýchlosť adaptácie aby sme získali čo najlepšie výsledky.
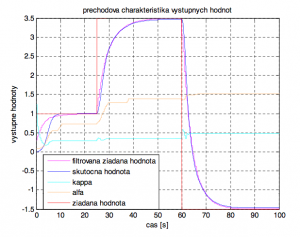
Obr. 2. Výstupné priebehy jednotlivých veličín z Maršíkovho algoritmu
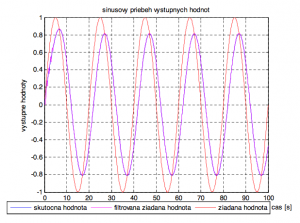
Obr. 3. Sínusový priebeh výstupných veličín z Maršíkovho algoritmu s periódou vzorkovania Ts=0.01
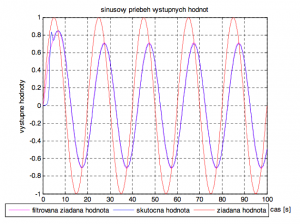
Obr. 4. Sínusový priebeh výstupných veličín z Maršíkovho algoritmu s periódou vzorkovania Ts=0.5
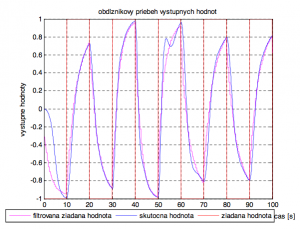
Obr. 5. Odĺžníkový priebeh výstupných veličín z Maršíkovho algoritmu s periódou vzorkovania Ts=0.5
Záver
Priebehy simulácií sú simulované v prostredí Matlab, s generátorom signálu a potom aj skokmi na vstupe, pri adaptačnej rýchlosti α = 0.1 až 100. Ďalej boli uvedené obrázky simulácií, kde sa rýchlosť adaptácie zvyšovala, znižovala a taktiež sa menila perióda vzorkovania. Rýchlosť adaptácie je veľmi dôležitá, ešte dôležitejšia je však miera kmitavosti pri heuristickom adaptívnom algoritme podľa Maršíka. Ten závisí okrem miery kmitavostí aj od ostatných adaptačných veličín, nachádzajúcich sa v algoritme.
Literatúra
- Doc. Ing MURGAŠ JÁN, CSc.; Ing HEJDA IVAN, CSc – ADAPTÍVNE RIADENIE TECHNOLOGICKÝCH PROCESOV, 1993, Str. 120,121
- Ing. ALEXÍK SAMUEL – DIZERTAČNÁ PRÁCA: MODIFIKÁCIE SAMONASTAVUJÚCICH SA HEURISTICKÝCH PID ALGORITMOV, Str. 50
- Ing. ALEXÍK SAMUEL – DIZERTAČNÁ PRÁCA: MODIFIKÁCIE SAMONASTAVUJÚCICH SA HEURISTICKÝCH PID ALGORITMOV, Str. 51
- Ing. ALEXÍK SAMUEL – DIZERTAČNÁ PRÁCA: MODIFIKÁCIE SAMONASTAVUJÚCICH SA HEURISTICKÝCH PID ALGORITMOV, Str. 78