Aplikácia DPCM a rovnomerného kódovania pri kompresii zvuku
03. Jún, 2013, Autor článku: Svetlíková Dominika, Informačné technológie, Študentské práce
Ročník 6, číslo 6  Pridať príspevok
Pridať príspevok
![]() Tento príspevok je zameraný na jednoduchú implementáciu predikčných techník kódovania zvuku, ktorý je v princípe náhodným signálom. V príspevku je popísaná teória optimálnej, ako aj suboptimálnej predikcie. Cieľom príspevku je overiť možnosť kompresie zvuku s využitím subobtimálnej predikcie a rovnomerného kódovania predikčných chýb. Ďalším cieľom je zistiť do akej miery je účinnosť kompresie závislá od vlastnosti vstupnej nahrávky pri zachovaní požadovanej kvality zvuku.
Tento príspevok je zameraný na jednoduchú implementáciu predikčných techník kódovania zvuku, ktorý je v princípe náhodným signálom. V príspevku je popísaná teória optimálnej, ako aj suboptimálnej predikcie. Cieľom príspevku je overiť možnosť kompresie zvuku s využitím subobtimálnej predikcie a rovnomerného kódovania predikčných chýb. Ďalším cieľom je zistiť do akej miery je účinnosť kompresie závislá od vlastnosti vstupnej nahrávky pri zachovaní požadovanej kvality zvuku.
Úvod
V klasickom nekomprimovanom zvukovom formáte wav je využitá pulzne kódová modulácia (PCM) . Každá diskrétna vzorka je vyjadrená pomocou kódového slova s dĺžkou 16b čo predstavuje 65536 zvukových úrovní. Vzorky nadobúdajú hodnotu z intervalu <-1,1>. Takto vyjadrený zvukový signál obsahuje veľa redundancie, ktorá vyplýva zo vzájomnej korelovanosti vstupných diskrétnych vzoriek. Táto redundancia je následne zbytočne kódovaná. Jednou z možnosti odstránenia redundancie je použitie niektorého zo skupiny entropických kódov. Ďalšou možnosťou je túto redundanciu odstrániť už na úrovni samotného signálu. Pri tomto prístupe je možné využiť niektorú ortogonálnu transformáciu, lineárnu predikciu alebo ich vzájomnú kombináciu [1]. Nevýhodou dekorelácie signálu pomocou diskrétnej ortogonálnej transformácie [4] je vyššia výpočtová náročnosť a zložitejšia implementácia. Na rozdiel od toho suboptimálna predikčná technika pozostáva z minimálneho počtu prvkov. V tomto príspevku sa budeme zaoberať iba technikou lineárnej predikcie.
1. Jednorozmerná optimálna lineárna predikcia
Bloková schéma lineárneho prediktora prvého rádu je na obr.1
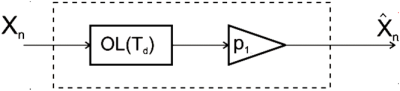
Obr. 1 Bloková schéma prediktora 1. rádu [2]
Z obrázku obr.1 je zrejmé, že výstupnú postupnosť možno zapísať takto:
| (1) |
kde p1 je predikčný koeficient, ktorý vo všeobecnosti pre s-rozmerný prediktor získame pomocou vzťahu:
| (2) |
kde je vektor koeficientov korelácie,
je matica koeficientov korelácie a
je vektor optimálnych predikčných koeficientov.
Jednotlivé prvky matice C vyrátame takto:
| (3) |
kde predstavuje disperziu vstupných náhodných vzoriek. Pre zjednodušenie implementácie namiesto optimálnej predikcie využijeme suboptimálnu predikciu.
2. Jednorozmerná suboptimálna predikcia
Pri suboptimálnej [1],[2] predikcii nie je potrebné poznať autokorelačnú funkciu, pretože predikcia sa vykonáva na základe predchádzajúcej vzorky bez násobenia, s predikčným koeficientom. Taká predikcia môže byť popísaná vzťahom:
| (4) |
Na obr.2 je zobrazený predikčný filter.
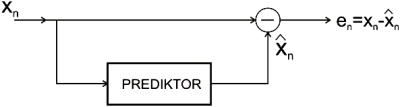
Obr. 2 Bloková schéma predikčného filtra na strane analýzy[2]
Z obr.2 je zrejmé, že na výstupe predikčného filtra budú chybové vzorky. Tieto chybové vzorky budú kvantované a kódované. V prípade, že n = 0, teda má byť predikčne kódovaná prvá vzorka postupnosti, na výstupe prediktora bude hodnota 0. Výsledná predikčná chyba bude potom rovná vstupnej vzorke. Z obr.2 ako aj vzťahu 4 vyplýva, že daný prediktor je možné implementovať pomocou oneskorovacieho člena s oneskorením rovným jednej vzorke.
Na nasledujúcom príklade je demonštrované ako predikčný filter funguje.Majme postupnosť vzoriek Xn=[1;1.2; 1; 0.8; 0.9; 1]. Keďže pri prvej vzorke na výstupe prediktora je nulová hodnota e0 = X0 – 0 = 1 – 0 = 1. Pri nasledujúcej vzorke X1 na výstupe prediktora bude hodnota X0 teda e1 = X1 – X0 = 1.2 – 1 = 0.2. Rovnakým postupom sa získajú ostatné vzorky chybovej postupnosti.Výsledná chybová postupnosť bude en =[1;0.2; -0.2; -0.2; 0.1; 0.1]. Na obr.3 je zobrazený predikčný filter zapojený na strane syntézy.
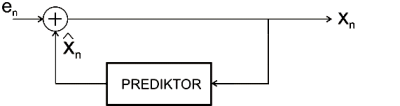
Obr. 3 Bloková schéma predikčného filtra na strane syntézy
Ako je z obr.3 zrejmé, chybová vzorka sa na strane syntézy sčítava s predikovanou. Prediktor na strane analýzy je identický s prediktorom na strane syntézy. Je nutné poznamenať, že predikčná filtrácia je bezstratová operácia. Nevýhodou takéhoto systému je pomerne malá odolnosť voči rušeniu v prenosovom kanáli pretože chyba, ktorá ovplyvní jednu vzorku postupnosti en sa prenesie do rekonštruovanej vzorky Xn , na základe, ktorej sa bude rekonštruovať ďalšia vzorka Xn+1. Takýmto spôsobom, hoci postupnosť chybových vzoriek už bude bez chýb, bude ovplyvnená celá výstupná postupnosť. Postupnosť Xn predchádzajúceho príkladu získame z chybovej postupnosti nasledovne: X0 = e0 + 0 =1+0=1. Pre nasledujúcu vzorku bude platiť X1 = e1 + X0 = 0.2 + 1 = 1.2 atď. Výsledná postupnosť syntézy bude identická so vstupnou postupnosťou analýzy.
3. Kvantovanie a kódovanie
Vzhľadom na veľmi malé hodnoty predikčných chýb sme navrhli kvantizátor [2] tak, že vstupný chybový signál je zosilnený a následne zaokrúhlený, čo sa dá zapísať nasledovne:
| (5) |
kde Nk predstavuje zosilnenie, en je chybová vzorka, K(n) kvantizačný index a operácia predstavuje zaokrúhlenie na najbližšie celé číslo. Zo vzťahu vyplýva, že kvantizačné indexy budú narastať s jednotkovým krokom. Potom pre určenie potrebného počtu bitov pre rovnomerné kódovanie všetkých indexov bude platiť vzťah:
| (6) |
kde Kmax a Kmin sú maximálna a minimálna hodnota kvantizačného indexu. Ďalším vyhodnocovaným parametrom je redukovaná dĺžka kódového slova[1] daná pomocou vzťahu:
| (7) |
kde m je pôvodná dĺžka kódového slova v prípade wav, m = 16b.Kompresný pomer v percentách je vyjadrený vzťahom:
| (8) |
4. Dosiahnuté výsledky
Na obr.4 je bloková schéma navrhnutého systému.
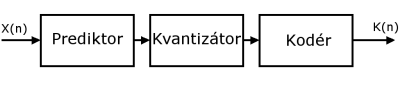
Obr. 4 Bloková schéma kódovacieho systému
Pre pokusy sme vybrali 4 pokusné skladby uvedené v Tab.1, ktoré sú rôznych hudobných žánrov a majú rôzny dynamický rozsah. Z dôvodu pamäťového obmedzenia PC budeme uvažovať vždy prvých 60 sekúnd skladby. Dynamický rozsah (DR) sme uvažovali ako strenú hodnotu z dynamického rozsahu ľavého a pravého kanálu. V našej aplikácii je DR definovaný vzťahom:
| (9) |
kde index k predstavuje ľavý alebo pravý kanál, Xi je hodnota i-tého prvku vstupnej nahrávky a Xmax je maximálna hodnota z absolútnej hodnoty vstupnej postupnosti nahrávky. Stredná hodnota DR pre obe kanály bude potom rovná
| (10) |
Ďalším parametrom, ktorý použijeme pri vyhodnocovaní výsledkov je odstup signálu od šumu S/Š[3],[4].
| (11) |
kde Xi je i-ta vzorka pôvodného signálu, je i-tá vzorka rekonštruovaného signálu.
Tab.1 Prehľad pokusných nahrávok
| Interpret | Názov skladby | Hudobný žáner | DR |
|---|---|---|---|
| Don Omar | Danzakuduro | Disco | 0.76 |
| Alice Cooper | Poison | Rock | 0.9 |
| HansZimmer | Time | Soundtrack | 0.37 |
| Neznámy | A od Prešova | Ľudova pieseň | 0.56 |
Pre vyhodnotenie sme empirickou metódou hľadali také Nk, aby odstup signálu od šumu bol minimálne 20dB a bola dosiahnutá čo najvyššia kompresia. Dosiahnuté výsledky sú uvedené v tab. 2.
Tab.2 Závislosť kompresie od DR
| Nahrávka | Nk | C (%) | R (bit) | S/Š (dB) | DR |
|---|---|---|---|---|---|
| Danzakuduro | 10500 | 87.5 | 2 | 22.66 | 0.76 |
| Poison | 22000 | 93.75 | 1 | 21.98 | 0.9 |
| Time | 70000 | 68 | 5 | 25.32 | 0.37 |
| A od Prešova | 25500 | 87.5 | 2 | 24.18 | 0.56 |
Z tab.2 je zrejmé, že najvyššia kompresia je dosiahnutá pri skladbe Time, ktorá má DR najnižší. Nízky DR neznamená nič iné ako to, že daná skladba je monotónna a neobsahuje prudké prechody z nevýraznej do výraznej pasáže. Naopak skladba Poison má vysoký DR teda v navrhnutom predikčnom systéme vznikajú chyby s veľkou hodnotou a tým vzniká potreba zvýšiť počet bitov, aby bolo možné tieto chyby v podobe kvantizačných indexov zakódovať.
Na obr.5 a obr.6 sú graficky znázornené jednotlivé pokusné nahrávky Poison a Time pred kompresiou, po kompresii a chybové signály, ktoré predstavujú šum vzniknutý kompresiou. Pre zjednodušenie uvádzame iba ľavý kanál.
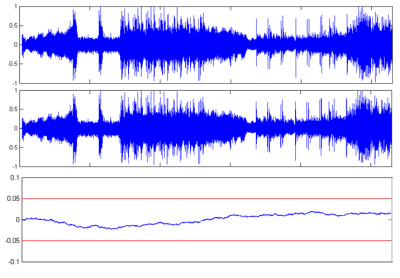
Obr. 5 Grafické znázornenie jedného kanála pokusnej nahrávky Poison (z hora) originálna nahrávka, komprimovaná nahrávka, chybový signál
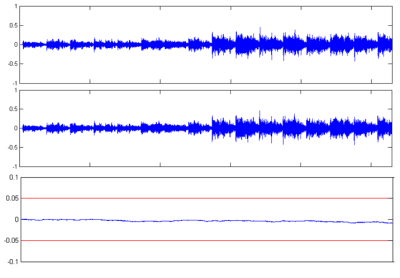
Obr. 6 Grafické znázornenie jedného kanála pokusnej nahrávky Time (z hora) originálna nahrávka, komprimovaná nahrávka, chybový signál
Záver
Cieľom príspevku bolo zistiť či je možné implementovať algoritmy jednorozmerného predikčného kódovacieho systému v spracovaní zvukového záznamu hudby. V článku sme to pre jednoduchosť ukázali s využitím jednorozmerného suboptimalného prediktora prvého rádu. Pre jednoduchosť sme na kódovanie predikčných chýb použili jednoduchý kód s pevnou dĺžkou kódového slova. Z výsledkov vyplýva, že rozhodujúcim faktorom pri kompresii je dynamický rozsah pokusnej nahrávky. Skladby, ktoré sú monotónne a k zmenám intenzity hlasu dochádza pozvoľne, majú DR nízky a kompresia je vysoká. Naopak pri skladbách ktoré obsahujú veľa prechodov z hlasných pasáží do tichých a naopak, majú DR vysoký a dosiahnutá kompresia je malá.
Zoznam použitej literatúry
- MIHALÍK,J.: Kódovanie obrazu vo videokomunikáciach, Mercury-Smékal, Košice, 2001, ISBN 80-89061-47-8.
- MIHALÍK, J., GLADIŠOVÁ, I.: Číslicové spracovanie signálov (Návody na cvičenia). LČSOV FEI TU Košice, 1998, ISBN 80-05-00275-0.
- MIHALÍK, J.ZAVACKÝ, J.GLADIŠOVÁ, I.: Signály a sústavy (Návody na cvičenia). LČSOV FEI TU Košice, 2004, ISBN 80-8073-138-1.
- MIHALÍK, J., ZAVACKÝ, J.: Diskrétne spracovanie signálov, LČSOV FEI TU, Košice, 2012, ISBN 978-80-553-0730-5.
Spoluautorom článku je Ing. Ondrej Kováč, Katedra elektroniky a multimediálnych telekomunikácií, Fakulta elektrotechniky a informatiky, Technická univerzita v Košiciach.

