Aj napriek tomu, že súčasné trendy hovoria o veľkom náraste bezhotovostných platobných operácií a o znížení významu peňažnej hotovosti, ľudia používajú hotovosť veľmi často a počet bankomatov na výber hotovosti neklesá. Pre banky je dôležité zvyšovať dostupnosť hotovosti prostredníctvom bankomatov pre široké vrstvy klientov a to tak dostupnosť v čase, ako aj lokálnu dostupnosť. Keďže banky sa v silnej konkurencii snažia o zvýšenie ziskov, je pre nich dôležité uspokojovať požiadavky klientov a zároveň optimalizovať náklady vo všetkých oblastiach. Efektívna správa bankomatov je aktuálnym problémom, ktorý v sebe integruje viacero aspektov počnúc bezpečnosťou bankomatov, bezpečnosťou užívateľov bankomatov, ako aj efektívna správa hotovosti. Tento článok je venovaný problematike správy hotovosti v bankomatoch a niektorým možným prístupom na zefektívnenie procesu distribúcie hotovosti.

Správu hotovosti v bankomatoch môžu banky zabezpečovať pre sieť svojich bankomatov vo vlastnej réžii, alebo to pre nich robia špeciálne spoločnosti. Workflow pre riadenie distribúcie hotovosti v bankomatoch prebieha cyklicky a má tieto základné fázy:

• nákup hotovosti a jej uloženie v trezoroch,
• výber skupiny bankomatov určených na obsluhu v danom časovom intervale,
• objednávanie distribučných vozidiel, plánovanie cesty,
• výmena boxov v bankomatoch,
• analýza zvyšnej hotovosti v boxoch a následná úprava predpovedných modelov.

Úlohou systému na správu hotovosti v bankomatoch je optimalizácia nákladov. Celý proces musí zohľadňovať náklady na transport (plánovanie), náklady na manipuláciu (logistiku) a náklady na tok peňazí (úroky, cena peňazí, penalizácie, a pod.). Každý z týchto faktorov je špecifický a prispieva k optimalizácii celého procesu. Zníženie nákladov v procese správy hotovosti je však možné jedine kombináciou týchto faktorov.

Transportné náklady sú tvorené priamymi nákladmi na prenájom vozidiel a ich prevádzku, vrátane personálnych nákladov na prevádzku vozidiel. V rámci tohto faktora je potrebné optimalizovať počet vozidiel a dobu ich prevádzky, ako aj dĺžku transportných trás.

Logistické náklady obsahujú náklady na manipuláciu vrátane zabezpečenia hotovosti pre prevoze, pri nakladaní hotovosti a pri samotnej výmene zapečatených boxov. Okrem toho je dôležitou súčasťou nákladov aj cena za dočasné uskladnenie v trezoroch. Do tejto oblasti patrí aj optimalizácia počtu trezorov a ich geografické rozmiestnenie vzhľadom na rozmiestnenie obsluhovaných bankomatov.

Náklady súvisiace s cenou hotovosti predstavujú náklady na nákup zapečatených boxov s hotovosťou, ktoré sa vymieňajú v bankomatoch. Informácia o množstve zvyšnej hotovosti v boxe nie je dostupná pri výmene boxu. Ak je box s hotovosťou vymenený skôr, ako to bolo potrebné, vzniká distribútorovi priama strata. Na druhej strane, v prípade, že distribútor nedoplní hotovosť do bankomatu včas a bankomat určitú dobu nevydáva peniaze, banka ho penalizuje. Preto podstatnou zložkou optimalizačného systému je model predpovedajúci vývoj výberov z bankomatov. Predpovedné modely pre vývoj výberov v bankomatoch sú založené na analýze dát získaných po otvorení zapečatených boxov a zistení zvyšnej hotovosti. Z týchto údajov je možné predpovedať typické cykly vyprázdňovania bankomatov v priebehu dňa, týždňa, mesiaca a roka.

Na vývoj výberov však majú vplyv aj niektoré mimoriadne udalosti z ktorých niektoré sú pravidelné – obdobie sviatkov, obdobie dovoleniek a školských prázdnin, niektoré čiastočne pravidelné, resp. opakujúce sa s veľkou časovou periódou a iné sú úplne výnimočné. Trendom je prepájanie predpovedných modelov na dostupné informačné zdroje, z ktorých je možné získať informácie o takýchto výnimočných udalostiach, ktoré môžu ovplyvniť vývoj výberu hotovosti z bankomatov. Najdôležitejším zdrojom takýchto informácií sú v súčasnosti webové sídla a sociálne siete. Z nich je možné získať informácie o pripravovaných podujatiach, ale aj o očakávanom množstve a zložení účastníkov pripravovaných podujatí. Tieto informácie výrazným spôsobom prispievajú k skvalitneniu predpovedných modelov a vstupujú do optimalizačného procesu správy hotovosti vo fáze výberu skupiny bankomatov pre obsluhu v danom časovom intervale.

Formulácia distribučného problému

Distribučný problém, resp. problém optimalizácie dopravných trás spadá do oblasti operačného výskumu a počítačovej vedy. Formulácia problému súvisí s problémom obchodného cestujúceho, ktorý je známy už od 19 teho storočia. V rokoch 1931-1932 bola v Nemecku publikovaná kniha „Problém obchodného cestujúceho, aký má byť a čo musí robiť aby mal úspech v svojom podnikaní. Skúsenosti vyslúžilého obchodného cestujúceho“, v ktorej sú sformulované základné princípy tejto kombinatorickej optimalizačnej úlohy [2]. Teoreticky sa tomuto problému venovali matematici už aj predtým. V roku 1856 anglický matematik W.R. Hamilton vynašiel matematickú hru, ktorej cieľom bolo nájsť cestu medzi hranami dvanásťstena tak, aby každý vrchol bol navštívený iba raz.

Ako optimalizačná úloha bol tento problém sformulovaný okolo roku 1930 s cieľom minimalizovať dĺžku trasy pri prechádzaní medzi jednotlivými vrcholmi grafu. Nájdenie minimálnej dĺžky trasy prehľadaním všetkých možností je úloha, ktorej komplexita narastá s pribúdajúcim počtom vrcholov superpolynomiálne. Preto sa pri riešení uplatňujú heuristické metódy. Tieto metódy je možné použiť aj na riešenie problému smerovania dopravných trás (VRP – z angl. Vehicle Routing Problem), ktorý predstavuje zovšeobecnenie problému obchodného cestujúceho pre skupinu vozidiel s určitými obmedzeniami. [1] Podľa charakteru obmedzení rozoznávame dalšie varianty problému smerovania dopravných trás, ako napr. problém s obmedzenými kapacitami áut, problém s časovými oknami (kedy je presne určený časový interval, v ktorom musia byť jednotlivé miesta obslúžené), problém so zberom a doručovaním a podobne.

Ilustračný príklad

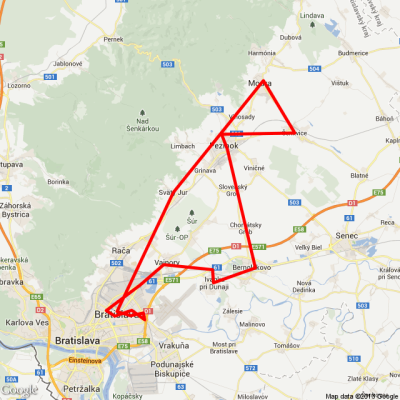
V tomto článku je použitý jeden zo scenárov projektu RPKOM, a to rozvoz finančnej hotovosti do bankomatov (ATM – Automated Teller Machines) prostredníctvom tretej osoby (na obr. 2 označená ako „ATM manažér“), tzn. chod bankomatu zabezpečuje bezpečnostná služba a nie banka samotná. Na testovanie bolo použité rozmiestnenie 120-tich bankomatov v Bratislavskom kraji [4] (obr. 1). Optimálny rozvoz a dopĺňanie finančných prostriedkov do jednotlivých bankomatov zahrňuje redukovanie nákladov spojených s hotovosťou (cena za nákup hotovosti, finančná strata za vrátenú hotovosť, penalizácia, atď.) a náklady vynaložené na prepravu (cena za prenájom vozidiel, cena paliva, mzda posádky, poistenie, atď.).

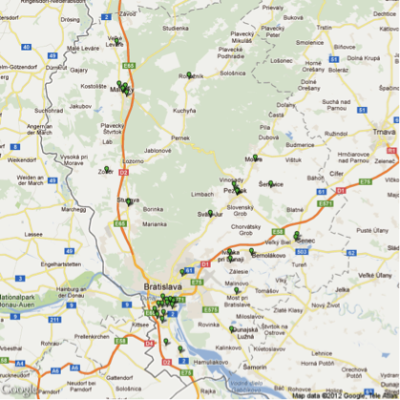
Obr. 1 Testovacia množina obslužných bodov a ich geografická poloha (120 bankomatov)

ATM manažér vykonáva rozhodnutia na základe informácií o cene služieb (pracovný čas, cena za prenájom vozidla, …) a na základe odhadu aktuálneho množstva hotovosti v jednotlivých bankomatoch. Tieto údaje sú vstupnými údajmi pre blok VRP, ktorého cieľom je optimalizovať jednotlivé okružné cesty s požiadavkou na časové intervaly, v rámci ktorých musia byť jednotlivé bankomaty obslúžené. Pri optimalizácii okružnej cesty sú uvažované nasledujúce podmienky:

• kapacita jednotlivých automobilov,
• pracovný čas, ktorý je rozdelený do troch osem hodinových intervalov,
• hodnota akceptovateľnej straty VAL, t.j. prijateľná hodnota straty za hotovosť vo vymenených boxoch.

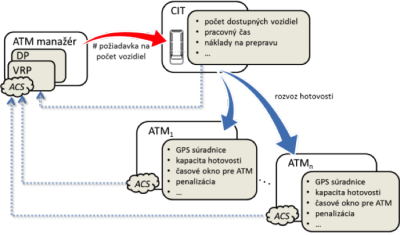
Obr. 2 Ilustračný obrázok opísaného dopravného problému

Návrh heuristických metód na riešenie distribučného problému

Označme množinu n obslužných bodov (bankomatov) P = {p₁, p₂, …, p_n}, kde každý obslužný bod p_i je definovaný GPS súradnicami p_i = (x_longitude, y_latitude). Najbližší bod bodu p_i∈P je bod p_j∈P – {p_i} definovaný tak, aby hodnota val(p_i, p_j) bola minimálna. Hodnota val(p_i, p_j) je vypočítaná podľa nasledujúceho vzorca:

(1)

kde dis(p_i, p_j) reprezentuje dĺžku cesty medzi bodom p_i a p_j a dur(p_i, p_j) reprezentuje čas za ktorý je možné túto trasu prejsť automobilom. Dĺžka cesty a čas potrebný na prejdenie daného úseku je získaný pomocou Google Maps API [6]. Koeficienty α a β transformujú hodnoty času (vzdialenosti) na finančné náklady. Na množinu bodov je aplikovaná metóda najbližších susedov, čám získame skupiny uzlov, ktoré je výhodné obslúžiť počas jednej cesty. Následne sa aplikuje metóda najbližších susedov, ktorá spája jednotlivé skupiny tak, aby boli splnené podmienky minimálnych nákladov a časové podmienky. Výsledkom je skupina cenovo výhodných okružných trás (obr. 3).

Obr. 3 Výsledok simulácie – zobrazenie okružnej cesty.

Ďalším cieľom je nájsť optimálne množstvo vozidiel vc s optimálnou množinou okružných ciest. Matematicky je možné problém formulovať nasledovne:

(2)

(3)

kde n reprezentuje počet okružných ciest, TC_i reprezentuje prepravné náklady i-tej okružnej cesty, Tt reprezentuje maticu časov prepravy medzi jednotlivými obslužnými bodmi dopravným vozidlom, Tw(t) predstavuje časové okno pre každé obslužné miesto (reprezentované prostredníctvom pravdepodobnosti prázdneho bankomatu), wt reprezentuje pracovný čas, p je množina obslužných bodov, ktoré je potrebné obslúžiť a t reprezentuje čas. Rovnica (2) vyjadruje nájdenie minimálnych prepravných nákladov n okružných ciest. Rovnica (3) reprezentuje minimálne množstvo vozidiel, ktoré sú schopné obslúžiť n okružných ciest s minimálnymi prepravnými nákladmi. Ak v rozhodovacom procese bude uvažovaná aj cena za prenájom vozidla, potom minimálne množstvo vozidiel je určené podľa nasledovnej rovnice:

(4)

kde TC reprezentuje cenu prepravy obslúženia jednotlivých uzlov prostredníctvom x vozidiel, FR reprezentuje cenu za prenajatie vozidla a PE reprezentuje penalizáciu za neobslúženie bankomatu. Navrhovaná metóda na nájdenie optimálneho počtu vozidiel a optimálnej množiny okružných trás musí vychádzať z toho, že rovnice (2) až (4) sú časovo závislé. V prípade dostupných informácií o aktuálnej dopravnej situácii na sledovanej trase, resp. predpovedaných dopravných oneskorení na jednotlivých úsekoch alebo dopravných obmedzeniach, je možné tieto informácie zahrnúť do rovnice (1).

Pre tento účel bol upravený ACO algoritmus (z ang. Ant Colony Optimization) . Princíp metódy ACO je odpozorovaný zo správania mravcov pri prehľadávaní priestoru za účelom nájdenia potravy. V prípade pozitívneho výsledku mravce na spiatočnej ceste do mraveniska (kratšia cesta) zanechávajú feromónovú značku, ktorá priťahuje ostatné mravce, čím sa intenzita feromónovej stopy zvyšuje. Po určitom čase je možné prehlásiť, že cesta s najvýraznejšou feromónovou značkou reprezentuje hľadané riešenie. Dôležitou vlastnosťou feromónov je ich vyprchávanie, čo sa tiež využíva pri aplikácii ACO algoritmov. Umelé mravce sa pri výbere cesty z bodu pi do bodu pj rozhodujú na základe pravdepodobnosti výberu danej vzťahom [3]:

(5)

kde je feromónový faktor na spojnici p_i-p_j a hodnota je vypočítaná zo vzťahu:

(6)

kde J_pi,pj je vzdialenosť medzi bodmi i a j. V našom prípade nahradíme vzdialenosť vo vzťahu (6) hodnotou vypočítanou podľa rovnice (1). Parametre α a β majú vplyv na relatívnu váhu feromónového faktora. Ak α=0, vyberie sa s najväčšou pravdepodobnosťou cesta do najbližšieho bodu. Naopak v prípade, že β=0, rozhodujúci je vplyv feromónovej značky. Aby sa zabránilo konvergencii metódy k sub-optimálnym riešeniam, feromónový faktor sa vypočítava podľa nasledujúceho vzťahu:

(7)

kde ρ je rýchlosť vyprchávania feromónu a je množstvo feromónu, ktoré je pridávané k-tym mravcom a vypočítava sa podľa vzťahu :

(8)

kde L_k je dĺžka k- tej cesty mravca. Podrobnejšie je táto metóda opísaná v [5].

Výsledky simulácií sú znázornené na obr. 4 a obr. 5. Modrá krivka reprezentuje prepravné náklady jednej pracovnej zmeny trvajúcej 8 hodín, čiarkovaná krivka reprezentuje hodnotu penalizácie. V tomto prípade je možné obslúžiť všetky obslužné body iba použitím viacerých vozidiel (napr. pri použití deviatich vozidiel prepravné náklady tvoria 990€ a penalizácia 4000€). Prepravné náklady pri dvojzmennej prevádzke sú znázornené hnedou krivkou. Použitím piatich vozidiel zabezpečíme obslúženie všetkých obslužných bodov bez penalizácie (prepravné náklady vo výške 1050€). Zelená krivka reprezentuje trojzmennú prevádzku, pričom jedna z nich je nadčas.

Prepravné náklady počas nadčasu sú vyššie ako počas pracovnej doby. V tomto prípade použitím štyroch vozidiel obslúžime všetky obslužné body, pričom prepravné náklady sú v hodnote 1200€. V týchto simuláciách nie je zahrnutá cena za prenájom vozidla (do úvahy sa berú iba parametre ovplyvňujúce prepravné náklady, pretože hľadáme optimálnu okružnú cestu). Pomocou nasledujúceho vzorca môžeme vypočítať hraničnú výšku poplatku za prenájom vozidla, aby bolo cenovo výhodné pracovať aj nadčas s menším počtom vozidiel:

(9)

kde TC sú prepravné náklady a FR reprezentuje poplatok za prenajatie automobilu na deň. Ak cena prenájmu je vyššia ako 150€, je cenovo efektívnejšie použiť štyri vozidlá a akceptovať prácu nadčas ako použiť päť automobilov. Na obr. 5 je znázornený výsledok simulácie prepravných nákladov v závislosti od počtu použitých automobilov pri akceptovaní nadčasov. Zelená krivka reprezentuje trojzmennú pracovnú dobu, hnedá (modrá) krivka reprezentuje dvoj (jedno)-zmennú prevádzku s jedno (dvoj)-zmenou prevádzkou nadčasov.

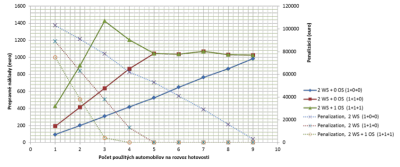
Obr. 4 Simulácia obslúženia všetkých obslužných bodov počas pracovnej doby a nadčasu v závislosti od počtu automobilov a dosiahnutá penalizácia

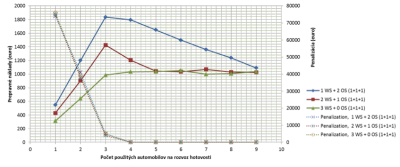
Obr. 5 Simulácia obslúženia všetkých obslužných bodov počas pracovnej doby a nadčasu v závislosti od počtu automobilov a dosiahnutá penalizácia

Z grafu je možné vidieť, že počet použitých automobilov môže ovplyvniť celkovú cenu prepravy. Napríklad prepravné náklady pri trojzmennej prevádzke (zelená krivka) a siedmich vozidlách sú 1000€ , zatiaľ čo prepravné náklady so štyrmi vozidlami sú 1040€ (je dôležité pripomenúť, že v tejto cene nie je zahrnutý poplatok za prenajatie auta). V nasledujúcej simulácii sa zisťoval vplyv akceptovateľnej hodnoty straty VAL na celkovú cenu prepravy vzhľadom na použitý počet vozidiel. V tomto prípade mala jedna tretina obslužných bodov nastavenú nízku hodnotu finančných prostriedkov a taktiež strmšiu krivku vyprázdňovania (pravdepodobnosť, že v danom bankomate nie je hotovosť). Simulovala sa trojzmenná pracovná doba. Výsledok simulácie je znázornený na obr. 6, ktorý môžeme rozdeliť na dve časti:

• použitím troch až piatich vozidiel na rozvoz hotovosti sa celkové prepravné náklady zvyšujú so zvyšujúcou sa hodnotou akceptovateľnej úrovne straty,
• v prípade použitia viacerých ako šiestich vozidiel na rozvoz hotovosti je vidieť, že vplyv optimalizačného algoritmu má väčší vplyv na prepravné náklady, ako hodnota akceptovateľnej straty (napr. prepravné náklady troch vozidiel a VAL = 100 sú 550€, ale prepravné náklady so šiestimi vozidlami a VAL = 700 sú 500€); je dôležité pripomenúť, že v tejto cene nie je zahrnutý poplatok za prenajatie auta).

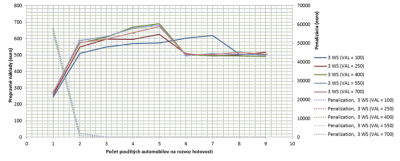
Obr. 6 Vplyv akceptovateľnej úrovne straty na celkové prepravné náklady

Poďakovanie

Táto publikácia je výsledkom implementácie projektu Výskum technológií pre riadenie podnikových procesov v heterogénnych distribuovaných systémoch v reálnom čase s podporou multimodálnej komunikácie, ITMS 26240220064 s podporou Operačného program výskum a vývoj Európskeho fondu regionálneho rozvoja. Podporujeme výskumné aktivity na Slovensku/Projekt je spolufinancovaný zo zdrojov EÚ.

Literatúra

1. Dantzig G. B. a Ramser J. H., The Truck Dispatching Problem, Management Science Vol. 6, No. 1 (Oct., 1959), pp. 80-91. (dostupné v júni 2014)
   http://andresjaquep.files.wordpress.com/2008/10/2627477-clasico-dantzig.pdf
2. Laporte G.: A Short History of the Traveling Salesman Problem, Canada Research Chair in Distribution Management, Centre for Research on Transportation (CRT) and GERAD HEC Montr ́eal, Canada. 2006 (dostupné v júni 2014)
   http://neumann.hec.ca/chairedistributique/common/laporte-short.pdf
3. Yaseen, S. G. , AL-Slamy N. M. A., Ant Colony Optimization, International Journale of Compter Science and Network Security, Vol. 8, No. 6, June 2008, pp.351-357.
4. Zelenka, J., – Budinská, I., – Dideková, Z. A combination of heuristic and non-heuristic approaches for modified vehicle routing problem. In LINDI 2012 : 4th IEEE International Symposium on Logistics and Industrial Informatics. – Piscataway : IEEE, 2012, p. 107-112. ISBN 978-1-4673-4517-0 (2012)
5. Zelenka, J., – Dideková, Z.. Cost balancing act of vehicle number to solve the vehicle routing problem with time windows. In INES 2013 : 17th IEEE International Conference on Intelligent Engineering Systems 2013. – Budapest : IEEE Industrial Electronic Society, 2013, p. 293-299. ISBN 978-1-4799-0830-1 (2013)
6. https://developers.google.com/maps/documentation/distancematrix/

---

Spoluautorom článku je Ivana Budinská, Ústav informatiky Slovenskej akadémie vied