Individualizácia simulátora subjektu s diabetom 1. typu, časť 2.

11. Máj, 2015, Autor článku: Tárník Marián, Informácie pre autorov, Medicína
Ročník 8, číslo 5 Pridať príspevok

p17958_icon Cieľom tejto práce je upraviť (individualizovať) parametre vybraných matematických modelov subjektu s diabetom 1. typu tak, aby ich výstupy zodpovedali dátam zo systému kontinuálneho monitorovania glykémie (CGM) od konkrétneho subjektu. Pre identifikáciu zodpovedajúcich podsystémov modelu sa tiež využijú dáta o farmakokinetike (PK, z angl. pharmacokinetics) a farmakodynamike (PD, z angl. pharmacodynamics) publikované v literatúre (viď. [8, 7]) konkrétneho inzulínu, ktorý používa subjekt. V predchádzajúcej časti sme sa zamerali na individualizáciu simulátora založeného na Bergmanovom modeli. V tejto časti je individualizovaný simulátor založený na Hovorkovom modely.

1. Simulátor s modelom podľa Hovorku

V tejto časti je opísaný model autorov Hovorka a kol. Pôvodne je model prezentovaný v článkoch [2, 3, 1]. V ďalšom je navrhnutý postup individualizácie tohto modelu tak aby v možnej miere zodpovedal konkrétnemu subjektu s diabetom 1. typu.

1.1. Opis modelu

1.1.1 Hovorkov model

Hovorkov model inzulín-glukózovej interakcie pozostáva z niekoľkých diferenciálnych rovníc. Model je možné rozdeliť na dve časti. Podsystém účinku (akcie) inzulínu a glukózový podsystém.

Podsystém účinku inzulínu

Podsystém účinku inzulínu pozostáva z troch diferenciálnych rovníc v tvare

$\dot X_1(t) = - k_{a1} X_1(t) + k_{a1} S_{I1} I(t)$

(1)

$\dot X_2(t) = - k_{a2} X_2(t) + k_{a2} S_{I2} I(t)$

(2)

$\dot X_3(t) = - k_{a3} X_3(t) + k_{a3} S_{I3} I(t)$

(3)

Signály ${X_1(t)}$ [1/min], ${X_2(t)}$ [1/min] a ${X_3(t)}$ [bezrozmerné] reprezentujú efekt inzulínu na distribúciu/transport glukózy, na odstraňovanie (spotrebu) glukózy a na vnútornú produkciu glukózy v uvedenom poradí, viď [3]. Parametre ${k_{a1}}$ [1/min], ${k_{a2}}$ [1/min] a ${k_{a3}}$ [1/min] sú obrátené hodnoty časových konštánt. Parameter ${S_{I1}}$ [l/mU/min] je inzulínová citlivosť distribúcie/transportu glukózy, parameter ${S_{I2}}$ [l/mU/min] je inzulínová citlivosť odstraňovania (spotreby) glukózy a ${S_{I3}}$ [l/mU] je inzulínová citlivosť vnútornej produkcie glukózy (EGP). Signál ${I(t)}$ [mU/l] je koncentrácia inzulínu v krvi.

Glukózový podsystém

Glukózový podsystém pozostáva z troch rovníc v tvare

$\dot Q_1(t) = - X_1(t) Q_1(t) + k_{12} Q_2(t) - F_{01}^c(t) -$

$- F_R(t) + EGP_0 \left( 1 - X_3(t) \right) + Ra(t)$

(4)

$\dot Q_2(t) = - X_2(t) Q_2(t) - k_{12} Q_2(t) + X_1(t) Q_1(t)$

(5)

$G(t) = \frac{Q_1(t)}{V_G}$

(6)

kde ${G(t)}$ [mmol/l] je koncentrácia glukózy v krvi (glykémia), ${Q_1(t)}$ [mmol] reprezentuje množstvo glukózy v dostupnom kompartmente, teda v kompartmente kde je dostupné (prebieha) meranie koncentrácie glukózy, a ${Q_2(t)}$ [mmol] reprezentuje množstvo glukózy v nedostupnom kompartmete, teda v tzv. periférnych tkanivách, kde sa koncentrácia glukózy nemeria. Parameter ${V_G}$ [l] je distribučný objem dostupného kompartmentu a parameter ${k_{12}}$ [1/min] udáva rýchlosť presunu glukózy z nedostupného do dostupného kompartmentu. Signál ${F_{01}^c}$ [mmol/min] je celkový tok glukózy daný spotrebou glukózy nezávislou na koncentrácii inzulínu. Je korigovaný vzhľadom na okolitú koncentráciu glukózy, potom

$F_{01}^c(t) = \left\{ \begin{aligned} &F_{01} & & \text{ak } G(t) \leq 4,5 \text{ [mmol/l]} \\ &F_{01} \frac{G(t)}{4,5} & & \text{inak} \end{aligned} \right.$

(7)

kde ${F_01}$ [mmol/min] je spotreba glukózy nezávislá na koncentrácii inzulínu. V pôvodných článkoch \cite{Hal.04,Hal.02} ${F_{01}^c = 0.0097 \, BW}$ kde ${BW}$ [kg] je telesná hmotnosť. Signál ${F_R(t)}$ [mmol/min] je tok glukózy vylučovanej obličkami ak je koncentrácia glukózy vyššia ako 9 [mmol/l]

$F_R(t) = \left\{ \begin{aligned} &0,003 \left( G(t) - 9 \right) V_G & & \text{ak } G(t) \geq 9 \text{ [mmol/l]} \\ &0 & & \text{inak} \end{aligned} \right.$

(8)

Tok glukózy ${EGP_0}$ [mmol/min] reprezentuje vnútornú produkciu glukózy extrapolovanú pre prípad nulovej koncentrácie inzulínu. V pôvodnom článku [3] hodnota ${EGP_0 = 0.0161 \, BW}$ . Nakoniec, ${Ra(t)}$ [mmol/min] je tok glukózy daný rýchlosťou vstrebávania glukózy do krvi (preto je označený rovnako ako táto veličina v predchádzajúcich modeloch). Aj v tomto prípade môže mať tento tok dva zdroje – vstrebávanie glukózy z tráviaceho traktu alebo priame intravenózne podávanie glukózy.

1.1.2 Podsystém vstrebávania inzulínu

Tento podsystém je rovnaký ako podsystém uvedený v predchádzajúcej časti článku, viď rovnice podsystému z rovnakým názvom. Jednotky veličín a parametrov sú však v tomto prípade rozdielne. Rýchlosť podávania inzulínu do podkožia ${v(t)}$ je v [mU/min]. Následne, množstvo inzulínu v kompartmentoch ${S_1(t)}$ a ${S_2(t)}$ je v [mU] a distribučný objem ${V_I}$ v [l]. Ako je uvedené vyššie koncentrácia inzulínu v krvi ${I(t)}$ je v [mU/l].

1.1.3 Podsystém vstrebávania glukózy

Podsystém vstrebávania glukózy je v tvare

$\dot D_1(t) = - \frac{1}{T_D} D_1(t) + A_G d(t)$

(9)

$\dot D_2(t) = - \frac{1}{T_D} D_2(t) + \frac{1}{T_D} D_1(t)$

(10)

$Ra(t) = \frac{1}{T_D} D_2(t)$

(11)

kde ${d(t)}$ [mmol/l] je rýchlosť podávania sacharidov v čase jedla, presnejšie, signál ${d(t)}$ je impulz so šírkou jednej periódy vzorkovania a s plochou zodpovedajúcou množstvu prijatých sacharidov. Pre konverziu medzi [mmol] a [g] sa uvažuje molekulárna hmotnosť glukózy ${180.16}$ [g/mol]. Parameter ${A_G}$ [bezrozmerné] je zlomok z množstva prijatých sacharidov, udáva koľko sacharidov sa efektívne vstrebalo, a ${T_D}$ [min] je časová konštanta podsystému. Signály ${D_1(t)}$ a ${D_2(t)}$ reprezentujú množstvo glukózy v kompartmentoch a ${Ra(t)}$ [mmol/min] je tok daný rýchlosťou vstrebávania glukózy do krvi (plazmy). Všimnime si, tento podsystém je v podstate tiež zhodný s podsystémom z predchádzajúcej časti článku. Keďže v tomto prípade ${Ra(t) = \frac{1}{T_D} D_2(t)}$ potom

$\dot Ra(t) = \frac{1}{T_D} \dot D_2(t)$

(12)

Dosadením rovnice (10) do (12)

$\begin{aligned} \dot Ra(t) &= \frac{1}{T_D} \left( - \frac{1}{T_D} D_2(t) + \frac{1}{T_D} D_1(t) \right) \\ &= \frac{1}{T_D} \left( - Ra(t) + D(t) \right) \end{aligned}$

(13)

kde sme zaviedli signál ${D(t)}$ [mmol/min] definovaný ako

$D(t) = \frac{1}{T_D} D_1(t)$

(14)

Následne

$\dot D(t) = \frac{1}{T_D} \dot D_1(t)$

(15)

a po substitúcii

$\begin{aligned} \dot D(t) &= \frac{1}{T_D} \left( - \frac{1}{T_D} D_1(t) + A_G d(t) \right) \\ &= \frac{1}{T_D} \left( - D(t) + A_G d(t) \right) \end{aligned}$

(16)

Nakoniec je možné písať podsystém vstrebávania glukózy v tvare ako v predchádzajúcej časti článku, teda

$\dot D(t) = - \frac{1}{T_D} D(t) + \frac{1}{T_D} A_G d(t)$

(17)

$\dot Ra(t) = - \frac{1}{T_D} Ra(t) + \frac{1}{T_D} D(t)$

(18)

1.1.4 Bazálny stav

Uvažujme, že bazálny (ustálený) stav simulátora subjektu s diabetom 1. typu založenom na modely podľa Hovorku je určený troma hodnotami. Rýchlosť podávania bazálneho inzulínu ${v_b}$ [mU/min], bazálna koncentrácia glukózy (bazálna glykémia) ${G_b}$ [mmol/l] a bazálna vnútorná produkcia glukózy ${EGP_b}$ [mmol/min]. Ide o podobný prístup ako je možné nájsť [6, 4, 5]. Hodnoty ${v_b}$ a ${G_b}$ sú špecifické parametre subjektu (pacienta) a sú teda známe. ${EGP_b}$ nie je možné odmerať, ani len odhadnúť, v podmienkach každodenného života a tento parameter je potrebné kvalifikovane zvoliť, viď [5]. V tomto prípade ${EGP_b}$ je definované v tvare

$EGP_b = EGP_0 \left( 1 - X_{3b} \right)$

(19)

kde ${X_{3b}}$ je hodnota signálu ${X_3(t)}$ v bazálnom stave. Zeveďme parameter ${EGP_{factor}}$ [bezrozmerné] tak aby

$EGP_0 = 0.0161 \cdot BW \cdot EGP_{factor}$

(20)

To znemená, že predpokladáme, že ${EGP_0}$ je zvolené ako zlomok štandardnej hodnoty ${EGP_0}$ aká je uvedená v pôvodných článkoch. Následne, ${EGP_b}$ je tým daná

$EGP_b = EGP_0 \left( 1 - S_{I3} I_b \right)$

(21)

kde sme použili fakt, že v bazálnom stave ${X_{3b} = S_{I3} I_b}$ . Bazálna koncentrácia inzulínu ${I_b}$ je jednoznačne daná rýchlosťou podávania bazálneho inzulínu ${v_b}$ a parametrami podsystému vstrebávania inzulínu. Tieto parametre boli pritom vyššie identifikované s využitím farmakokinetiky inzulínu. V bazálnom stave je podsystém vstrebávania inzulínu možné písať v tvare

$0 = - \frac{1}{T_I} S_{1b} + v_b$

(22)

$0 = - \frac{1}{T_I} S_{1b} + \frac{1}{T_I} S_{2b}$

(23)

$0 = - k_I I_b + \frac{1}{T_I} \frac{1}{V_I} S_{2b}$

(24)

preto potom

$I_b = \frac{1}{k_I} \frac{1}{V_I} v_b$

(25)

Keďže bazálna glykémia ${G_b}$ je známa, tak je známa aj bazálna hodnota signálu ${Q_1(t)}$ , teda ${Q_{1b}}$

$Q_{1b} = G_b V_G$

(26)

V bazálnom stave je možné glukózový podsystém možné písať v tvare

$0 = - S_{I1} I_b Q_{1b} + k_{12} Q_{2b} - F_{01} + EGP_b$

(27)

$0 = S_{I1} I_b Q_{1b} - k_{12} Q_{2b} - S_{I2} I_b Q_{2b}$

(28)

kde sa predpokladá ${G_b \geq 4.5}$ [mmol/l] a nulové renálne vylučovanie glukózy, teda ${G_b \leq 9}$ [mmol/l]. V bazálnom stave tiež platí ${S_{I1} I_b = X_{1b}}$ a ${S_{I2} I_b = X_{2b}}$ . Parametre ${S_{I1}}$ , ${S_{I2}}$ a ${S_{I3}}$ súvisia s inzulínovou citlivosťou vo všeobecnosti a teda su špecifické pre daný subkjekt, obdobie dňa atď. Tu predpokladáme, že tieto parametre sú dané (alebo skôr zvolené). Ako bolo uvedené vyššie ${Q_{1b}}$ je známe. Hodnotu ${Q_{2b}}$ a parameter ${k_{12}}$ je možné dopočítať. Z rovnice (27) máme

$k_{12} Q_{2b} = S_{I1} I_b Q_{1b} + F_{01} - EGP_b$

(29)

Dosadením do rovnice (28)

$0 = S_{I1} I_b Q_{1b} - S_{I1} I_b Q_{1b} - F_{01} + EGP_b - S_{I2} I_b Q_{2b}$

(30)

$0 = - F_{01} + EGP_b - S_{I2} I_b Q_{2b}$

(31)

$Q_{2b} = \frac{- F_{01} + EGP_b}{S_{I2} I_b}$

(32)

Nakoniec

$k_{12} = \frac{S_{I1} I_b Q_{1b} + F_{01} - EGP_b}{ Q_{2b}}$

(33)

Týmto je výpočet hodnôt bazálneho stavu modelu úplný. Pri výpočte sa uvažuje nulová hodnota ${Ra(t)}$ v bazálnom stave.

1.2. Prispôsobenie parametrov modelu

Najskôr sumarizujme parametre, ktoré sú známe alebo zvolené ako priemer v populácii. Ako bolo uvedené v predchádzajúcom, ${BW = 64,6}$ [kg], ${v_b = 1,09}$ [U/h] a ${G_b = 8,5}$ [mmol/l]. Ďalej, distribučný objem ${V_G = 0,1467 \, BW}$ [l], spotreba glukózy nezávislá od koncentrácie inzulínu ${F_{01} = 0,0097 \, BW}$ [mmol/min] a ${A_G = 0,95}$ [bezrozmerné].

1.2.1 Podsystém vstrebávania inzulínu

Vzhľadom na to, že ide o ten istý podsystém ako v predcházdajúcej časti, rovnaká procedúra identifikácie sa uplatňuje aj v tomto prípade s rovnakými výsledkami. Pre úplnosť uvádzame hodnoty veličín parametrov použitých v tomto prípade. Máme ${v_b = 1,09}$ [U/h] čo znamená ${v_b = 18,1666}$ [mU/min]. Identifikované parametre podsystému sú ${T_I = 44,55}$ [min], ${k_I = 0,1645}$ [1/min] a ${V_I = 138,8}$ [dl/kg] čo znamená ${V_I = 0,1388 \, BW}$ [l].

1.2.2 Identifikácia všetkých parametrov v jednom kroku

V predchádzajúcej časti je simulátor s Bergmanovým modelom identifikovaný v troch hlavných krokoch. V prvom kroku sú použité PK dáta (farmakokinetika) pre identifikáciu podsystému vstrebávania inzulínu. Ako sme uviedli vyššie, rovnakú procedúru je možné uplatniť aj pri podsystéme v simulátore založenom na Hovorkovom modeli z rovnakými výsledkami. Ak je Bergmanov model v bazálnom stave signál účinku (akcie) inzulínu ${X(t)}$ je nulový. Inými slovami ${X(t)}$ je nenulový len ak sa rýchlosť podávania inzulínu ${v(t)}$ líši od bazálnej rýchlosti podávania inzulínu. Je možné povedať, že táto skutočnosť oddeľuje účinok bazálneho a bolusového inzulínu. Preto je možné tiež oddeliť aj glukózový tok spôsobený odchýlkou koncentrácie inzulínu od bazálnej koncentrácie (odchýlkou spôsobenou bolusom). To následne umožňuje určiť parametre modelu, ktoré v princípe súvisia s farmakodynamikou a použiť PD dáta (farmakodynamiku) pre ich identifikáciu.

V Hovorkovom modely sú signály účinku (akcie) inzulínu ${X_1(t)}$ , ${X_2(t)}$ a ${X_3(t)}$ nulové len ak je koncentrácia inzulínu ${I(t)}$ nulová. Nulová koncentrácia inzulínu však nie je akceptovateľný bazálny stav. Preto oddelenie efektu bazálneho a bolusového inzulínu v tomto prípade nie je možné tak ako v prípade Bergmanovho modelu. Preto v tejto časti identifikujeme všetky parametre simulátora s Hovorkovým modelom v jednom kroku naraz. Identifikácia je založená výlučne na CGM dátach. Cieľ je identifikovať vektor neznámych parametrov

$\Theta_4 = \begin{bmatrix} S_{I1} & S_{I2} & S_{I3} & EGP_{factor} & k_{a1} & k_{a2} & k_{a3} & T_D \end{bmatrix}^\mathsf T$

(34)

tak aby odchýlka medzi nameranými CGM dátami a výstupom simulátora bola minimalizovaná. Pre veľký počet identifikovaných parametrov je možné očakávať, že obmedzenia hodnôt parametrov budú hrať významnú úlohu v optimalizačnom probléme. Je zrejmé, že všetky identifikované parametre sú kladné, teda ${\Theta_4 > 0}$ . Parameter ${k_{12}}$ je funkciou vektora ${\Theta_4}$ keďže je závislý na zvolených bazálnych hodnotách a niekoľkých parametroch modelu. Navyše, parameter ${k_{12}}$ musí byť tiež kladný, ${k_{12} > 0}$ . Ak by bol ${k_{12}}$ záporný tak smer toku, ktorého rýchlosť tento parameter udáva, by bol opačný, čo v modely nie je dovolené. V bazálnom stave by mala byť vnútorná produkcia glukózy vyššia ako konštantná spotreba glukózy nezávislá na koncentrácii inzulínu ${F_{01b}}$ (kde ${{}_b}$ značí bazálnu hodnotu), teda ${EGP_b \geq F_{01b}}$ .

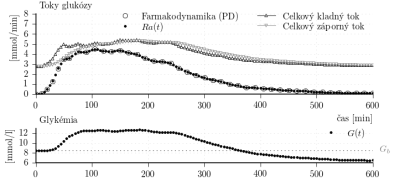
Obr. 1: Výsledky simulačného experimentu v ktorom je simulátor s Hovorkovým modelom, s parametrami z tabuľky 1, použitý pre simuláciu experimentu merania farmakodynamiky inzulínu.

Tab.1: Sumár hodnôt parametrov identifikovaných v časti 1.2.2.

Parameter	Hodnota	Jednotka
${S_{I1}}$	2.1594e-03	[l/mU/min]
${S_{I2}}$	1.3994e-12	[l/mU/min]
${S_{I3}}$	3.6377e-02	[l/mU]
${k_{a1}}$	7.7455e-04	[1/min]
${k_{a2}}$	1.8215e-01	[1/min]
${k_{a3}}$	2.0118e-02	[1/min]
${EGP_{factor}}$	1.1261	[-]
${T_D}$	35.5118	[min]

Úloha môže byť formulovaná ako problém nelinéarnej metódy najmenších štvorcov v tvare

$\begin{aligned} &\text{min} & & \Phi \\ &\text{s. t.} & & \Theta_4 > 0 \\ & & & k_{12} > 0 \\ & & & EGP_b \geq F_01 \end{aligned}$

(35)

kde účelová funkcia ${\Phi}$ je v tvare

$\Phi = \left\| y - \hat y(\Theta_4) \right\|^2$

(36)

kde ${y}$ je vektor nameraných CGM dát a ${\hat y}$ je vektor simulovanej glykémie. V tomto prípade bola použitá simplexová metóda (downhill simplex algorithm), ako je implementovaná v knižnici SciPy pre Python, pre minimalizáciu funkcie v tvare

$\Phi(\Theta_4) = \left\{ \begin{aligned} &10^{10} & & \text{if } \Theta_4 < 0 \\ &10^{10} & & \text{if } k_{12} \leq 0 \\ &10^{10} & & \text{if } EGP_b \leq F_{01} \\ & \left\| y - \hat y(\Theta_4) \right\|^2 & & \text{otherwise} \end{aligned} \right.$

(37)

Výsledné parametre sú sumarizované v tabuľke 1. Výstup simulátora s výslednými parametrami je graficky porovnaný s CGM dátami, použitými pre identifikáciu, na obr. 2.

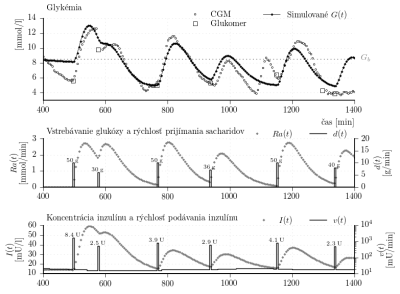
Obr. 2: Výsledky identifikácie simulátora s modelom podľa Hovorku. Procedúra identifikácie je opísaná v časti 1.2.2. Identifikované parametre modelu sú sumarozované v tabuľke 1.

Identifikovaný simulátor môže byť ohodnotený využitím metrík, ktoré sú uvedené v predchádzajúcej časti. V tomto prípade ${\text{VAF} = 76,85}$ [%], ${\text{RMSE} = 1,14}$ [mmol/l] a ${\text{SFM} = 51,82}$ [%]. Tieto výsledky sú lepšie v porovnaní s verifikáciou simulátora založeného na Bergmanovom modely. Hlavným dôvodom je, že jediným cieľov pri tejto identifikácii je zhoda s CGM dátami. Napríklad farmakodynamika inzulínu nie je pri identifikácii priamo zohľadnená.

Simulujme experiment zodpovedajúci priebehu merania farmakodynamiky, presnejšie, v simulácii použime ako vstup farmakodynamiku, teda priebeh intravenóznej infúzie glukózy (signál ${Ra(t)}$ ). Parametre pritom použime z tabuľky 1. Výsledky sú znázornené na obr. 1. Na obr. 1 sú zobrazené aj toky glukózy dostupného kompartmentu modelu (kompartment plazmy). V rovnici je celkový kladný tok glukózy daný výrazmi ${k_{12} Q_2(t) + EGP_0(1 - X_3(t)) + Ra(t)}$ a celkový záporný tok daný ako ${X_1(t) Q_1(t) - F_{01}^c(t)}$ . Je zrejmé, že simulátor nezodpovedá farmakodynamike inzulínu. Glykémia sa počas experimentu neudržiava na bazálnej hodnote. Toto je indikáciou, že inzulínová citlivosť modelu a dynamika účinku inzulínu nezodpovedajú priemerným charakteristikám farmakodynamiky inzulínu použitého v tomto prípade.

1.2.3 Identifikácia v dvoch krokoch

Parametre modelu je možné identifikovať aj spôsobom, v ktorom zohľadníme farmakodynamiku inzulínu. Sú pre to potrebné dva kroky.

Identifikácia založená na FD dátach

V experimente pre meranie farmakodynamiky sa používa intravenózne podávanie glukózy. Signál ${Ra(t)}$ preto nie je výstupom podsystému vstrebávania glukózy. Následne, pri identifikácii založenej na FD dátach parameter ${T_D}$ je potrebné vylúčiť z vektora neznámych parametrov pretože nemá vplyv na účelovú funkciu. Napriek faktu, že v tomto kroku je identifikácia založená na FD dátach je potrebné identifikovať aj parametre súvisiace s vnútornou produkciou glukózy (ktorá nesúvisí priamo s farmakodynamikou). Dôvodom je nemožnosť oddeliť efekty bolusového a bazálneho inzulínu ako bolo diskutované vyššie. V tomto kroku je cieľom identifikovať vektor neznámych parametrov

$\Theta_5 = \begin{bmatrix} S_{I1} & S_{I2} & S_{I3} & EGP_{factor} & k_{a1} & k_{a2} & k_{a3} \end{bmatrix}^\mathsf T$

(38)

tak aby bola odchýlka medzi ${G(t)}$ a ${G_b}$ minimalizovaná. Problém je možné sformulovať podobne ako v predchádzajúcej časti, teda minimalizuje sa funkcia v tvare

$\Phi(\Theta_5) = \left\{ \begin{aligned} &10^{10} & & \text{ak } \Theta_5 < 0 \\ &10^{10} & & \text{ak } k_{12} \leq 0 \\ &10^{10} & & \text{ak } EGP_b \leq F_{01} \\ & \left\| G_b - \hat y(\Theta_5) \right\|^2 & & \text{inak} \end{aligned} \right.$

(39)

kde ${\hat y}$ je vektor simulovanej glykémie. Pre minimalizáciu účelovej funkcie ${\Phi(\Theta_5)}$ sa použila simplexová metóda (downhill simplex algorithm) ako je implementovaná v knižnici SciPy pre Python.

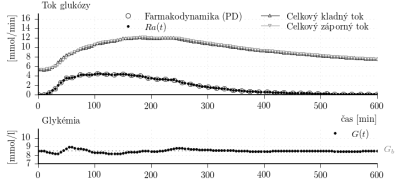
Obr. 3: Výsledok identifikácie založenej na FD dátach.

Výsledné parametre sú v tabuľke 2. Výsledky tiež na obr. 3. Je možné vidieť, že simulovaná glykémia ${G(t)}$ sa udržiava v užšom pásme okolo bazálnej hodnoty ${G_b}$ ako pri simulácii s modelom podľa Bergmana. Sú zobrazené aj toky glukózy dostupného kompartmentu modelu (kompartment plazmy). V rovnici je celkový kladný tok glukózy daný výrazmi ${k_{12} Q_2(t) + EGP_0(1 - X_3(t)) + Ra(t)}$ a celkový záporný tok daný ako ${X_1(t) Q_1(t) - F_{01}^c(t)}$ .

Tab.2: Parametre identifikované v časti 1.2.3.

Parameter	Hodnota	Jednotka
${S_{I1}}$	4.6710e-03	[l/mU/min]
${S_{I2}}$	2.5760e-04	[l/mU/min]
${S_{I3}}$	3.7628e-03	[l/mU]
${k_{a1}}$	3.1293e-03	[1/min]
${k_{a2}}$	2.2312e-10	[1/min]
${k_{a3}}$	9.8681e-01	[1/min]
${EGP_{factor}}$	2.1183	[-]
${T_D}$	27.1884	[min]

Identifikácia založená na CGM dátach

Druhým krokom je identifikácia ostávajúceho parametra ${T_D}$ . Identifikácia je založená na CGM dátach, rovnako ako v časti 1.2.2. Parametre identifikované v predchádzajúcej časti sú použité v modely. Cieľom je identifikovať parameter ${T_D}$ tak aby bola odchýlka medzi nameranými CGM dátami a simulovanou glykémiou minimalizovaná. Pre jednoduchosť použijeme rovnakú procedúru ako v časti, pričom vektor ${\Theta_5}$ je nahradený parametrom ${T_D}$ . Výsledné parametre sú v tabuľke 2. Výstup simulátora s týmito parametrami je graficky porovnaný s CGM dátami na obr. 4. Výsledky verifikácie sú ${\text{VAF} = 51.26}$ [%], ${\text{RMSE} = 1.76}$ [mmol/l] a ${\text{SFM} = 26.03}$ [%] čo je porovnateľné s výsledkami verifikácie simulátora s modelom podľa Bergmana.

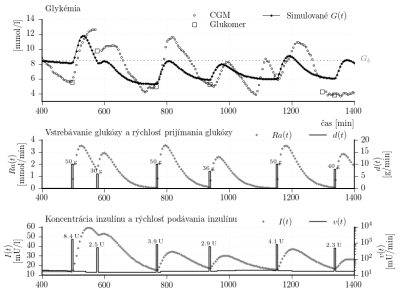
Obr. 4: Porovnanie CGM dát s výstupom individualizovaného simulátora založeného na Hovorkovom modely. Parametre simulátora sú sumarizované v tabuľke 2.

2. Záver

Cieľom tejto práce, ktorá sa skladá z dvoch častí, bolo prispôsobenie parametrov dvoch simulátorov diabetu tak, aby výstup zodpovedal konkrétnemu subjektu. Modely, ktoré sú základom simulátorov reprezentujú vo všeobecnosti priemerného pacienta, pretože ich autori určovali parametre z priemerných dát od väčšieho množstva subjektov. V prvom prípade je jadrom simulátora Bergmanov minimálny model, v druhom je to Hovorkov model. Subsystém pre vstrebávanie sacharidov z tráviaceho traktu a subsystém vstrebávania inzulínu z podkožia je pri oboch simulátoroch rovnaký.

Navrhli sme postup, ako pomocou dostupných informácií dospieť k individualizovaným parametrom týchto simulátorov. Za dostupné informácie považujeme informáciu o používanom inzulíne, a teda informáciu o jeho farmakokinetike a farmakodynamike (z literatúry), informácie o prijatých sacharidoch, informácie o glykémii z CGM systému a glukometra, informáciu o priemernej rýchlosti podávania bazálneho inzulínu (z inzulínovej pumpy) a bazálnu glykémiu (prípadne cieľovú glykémiu). Dá sa skonštatovať, že sa jedná o dáta zo štandardného diabetického denníka a inzulínovej pumpy. V prvom kroku individualizácie sme identifikovali parametre podsystému vstrebávania inzulínu na základe farmakokinetiky inzulínu. Tento podsystém nie je ovplyvňovaný ostatnými časťami modelu. Platí to pre oba uvedené simulátory.

Pri simulátore s Bergmanovým modelom je navrhnutý postup identifikácie jednoznačný. Z informácie o farmakodynamike inzulínu bolo možné identifikovať parametre ovplyvňujúce dynamiku účinku inzulínu. Zvyšné parametre sme identifikovali s využitím nameraného priebehu glykémie. Pomocou validácie individualizovaného simulátora s Bergmanovým modelom sme ukázali, že ak na priebeh glykémie vplývajú prevažne faktory, s ktorými počíta model, simulátor vystihuje priebeh glykémie, viď dni D00 či D01. Samozrejme, ak vplývajú aj iné faktory, ktorých vplyv je možné predpokladať v dni D04, simulácia nedostatočne vystihuje skutočnú glykémiu. Stále však platí, že hlavné faktory sú simulátorom vystihnuté. To umožňuje pozorovať aký veľký vplyv majú, v niektorých časových obdobiach, iné, nemodelované faktory. Pri návrhu postupu pre individualizáciu simulátora s Hovorkovým modelom sme konštatovali, že nie je možné jednoznačne zvoliť postup individualizácie. Preto sme overili dva postupy.

V prvom sme identifikovali všetky parametre na základe CGM dát v jednom kroku. Výstupná glykémia z modelu pomerne presne fituje namerané dáta. Avšak napríklad pri nasimulovaní experimentu pre získanie farmakodynamiky inzulínu dostávame úplne odlišné glukózové toky (glukóza vstupujúca do systému v porovnaní s glukózou vystupujúcou zo systému), čo nie je prijateľné ako výsledok simulácie tohto experimentu. Indikuje to, že tento postup nevedie k výsledku, ktorý by zohľadňoval všetky dostupné informácie, teda aj dáta o farmakodynamike. Hlavné kritérium, teda fitovanie priebehu glykémie, je však splnené veľmi dobre.

Druhý postup sa skladá z dvoch krokov. Najskôr identifikujeme zodpovedajúce parametre s tým, že hlavným kritériom sú výsledky simulácie experimentu merania farmakodynamiky. Až následne sú zvyšné parametre identifikované tak aby sa simulovaná glykémia približovala k nameranej. Tento postup nie je zhodný s postupom pre simulátor s Bergmanovým modelom. V tomto prípade nie je jednoznačné ako využiť informáciu o farmakodynamike (pri Bergmanovom modeli je). Napríklad by tiež bolo možné váhovať vplyv kritéria súvisiaceho s farmakodynamikou vzhľadom na vplyv kritéria fitovania nameranej glykémie.

Výsledky dosiahnuté navrhnutým postupom sú prakticky zhodné s výsledkami individualizácie simulátora s Bergmanovým modelom. To ukazuje, že aj simulátor s Hovorkovým modelom zohľadňuje všetky informácie uvažované pri individualizácii. Nami navrhnutý postup je možné, samozrejme, aplikovať aj pre iných pacientov a iný typ inzulínu. Predpokladom je len znalosť vstupných informácii potrebných pre prispôsobenie simulátorov danému pacientovi.

Poďakovanie

Článok je jedným z výstupov výskumnej práce projektu s názvom “Centrum výskumu závažných ochorení a ich komplikácií”, “ITMS projektu: 26240120038″. “Projekt je spolufinancovaný zo zdrojov EÚ. Podporujeme výskumné aktivity na Slovensku”.

Literatúra

R. Hovorka, F. Shojaee-Moradie, P. V. Carroll, L. J. Chassin, I. J. Gowrie, N. C. Jackson, R. S. Tudor, A. M. Umpleby, and R. H. Jones. Partitioning glucose distribution/transport, disposal, and endogenous production during ivgtt. American Journal of Physiology – Endocrinology and Metabolism, (282):E992–E1007, January 2002.
Roman Hovorka. Management of diabetes using adaptive control. International Journal of Adaptive Control and Signal Processing, 19(5):309–325, 2005.
Roman Hovorka, Valentina Canonico, Ludovic J Chassin, Ulrich Haueter, Massimo Massi-Benedetti, Marco Orsini Federici, Thomas R Pieber, Helga C Schaller, 10 Lukas Schaupp, Thomas Vering, and Malgorzata E Wilinska. Nonlinear model predictive control of glucose concentration in subjects with type 1 diabetes. Physiological Measurement, 25(4):905, 2004.
L. Magni, D.M. Raimondo, L. Bossi, C.D. Man, G.D. Nicolao, B. Kovatchev, and C. Cobelli. Model predictive control of type 1 diabetes: An in silico trial. Journal of Diabetes Science and Technology, 1(6), November 2007.
C.D. Man, D.M. Raimondo, R.A. Rizza, and C. Cobelli. Gim, simulation software of meal glucose-insulin model. Journal of Diabetes Science and Technology, 1(3), May 2007.
C.D. Man, R.A. Rizza, and C. Cobelli. Mixed meal simulation model of glucoseinsulin system. In Engineering in Medicine and Biology Society, 2006. EMBS ’06. 28th Annual International Conference of the IEEE, pages 307–310, 30 2006-sept. 3 2006.
S.R. Mudaliar, F. A. Lindberg, M. Joyce, P. Beerdsen, P. Strange, A. Lin, and R. R. Henry. Insulin aspart (b28 asp-insulin): A fast-acting analog of human insulin. Diabetes Care, 22(9):1501–1506, September 1999.
Novo-Nordisk. NovoRapid (insulin aspart) – Product Monograph. Watermeadow Medical, Two Rivers House, Station Lane, Witney, Oxfordshire OX28 4BH, UK on behalf of Novo Nordisk A/S, 2002.

Spoluautorom článku je Tomáš Ludwig, Ústav robotiky a kybernetiky, Fakulta elektrotechniky a informatiky, Slovenská technická univerzita v Bratislave

O časopise

Meta

RSS

Individualizácia simulátora subjektu s diabetom 1. typu, časť 2.

Napísať príspevok

Rubriky

Burza práce

Štúdijné materiály

Archív