Cieľom práce je naznačiť využitie akceloremetra pri získavaní informácie o aktuálnej polohe bremena portálového žeriava, respektíve o frekvencii jeho kmitov, objasniť možnosti spracovania výstupného signálu, priblížiť metódy merania frekvencie ako aj zhodnotiť vhodnosť jeho použitia v praxi.

Úvod

Akcelerometer je technické zariadenie používané na meranie zrýchlenia, náklonu, uhla vychýlenia, natočenia, meranie otrasov ako i na meranie samotnej gravitácie. Je využiteľný v širokej škále technických odvetví ako robotika (meranie aktuálnej polohy, náklonu), letectve (autopilot), automobilizme (alarmy, airbagy), mobilných telefónoch, herných konzolách, používajú sa tiež na monitorovanie ľudského pohybu a spolu s inými senzormi (gyroskopy) sú súčasťou meracích a detekčných sústav.

Podľa fyzikálnej podstaty na základe, ktorej pracujú ich môžeme rozdeliť do viacerých kategórii: Kapacitné, piezoelektrické, piezosenzitívne, tepelné. Použitý MEMS akcelerometer sa radí ku kapacitným senzorom zrýchlenia. V súčasnosti patria kapacitné snímače typu MEMS medzi najpoužívanejšie. Základný princíp merania akcelerometra je využívanie prítomnosti gravitácie, a jej rozkladu do jednotlivých osí, v závislosti od natočenia senzora.

Zisťovanie uhlov natočenia k osiam

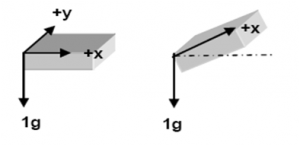
Skôr ako bude detailnejšie opísaný výpočet uhlov trojosového akcelerometra, je potrebné načrtnúť nevýhody jednoosového snímača a následnú nutnosť použitia viacosového meracieho snímača pre potreby merania uhla natočenia. V prípade použitia jednoosového akcelerometra sa využíva zvislosť gravitácie (ak je teda prítomná) pričom meranie je limitované na jednu os, ako je to načrtnuté na obrázku č.1. Z obrázku vidno, že akcelerometer je otáčaný okolo osi y, pričom sa mení uhol k osi x. Pri tomto otáčaní zostáva os y na hodnote 0g (presnejšie zložka gravitačného zrýchlenia v tomto smere).

Obr.1:Jednoosí akcelerometer

Keďže ide iba o jednoosí akcelerometer je možné merať iba jednu zo zložiek gravitačného zrýchlenia, v tomto prípade jeho sínusový priemet. Uhol vychýlenia medzi nakloneným akcelerometrom a osou x je teda možné vypočítať z výstupného údaja A_x podľa vzťahu: . Závislosť nameraného priemetu gravitačného zrýchlenia od uhla natočenia prístroja však ukazuje nerovnomernú presnosť merania. Presnosť klesá medzi -90° a -45° a medzi 45° a 90°.

Táto metóda sa teda stáva nepresnou pri hodnotách blízkych hodnotám +1g a -1g. Ďalšou nevýhodou je nemožnosť zistenia kvadrantu, v ktorom sa uhol vychýlenia nachádza pri požadovanej plnej rotácii. Jednoosový akcelerometer je maximálne vhodný na meranie výchyliek od -45° do +45°.

Východiskom z problému neznalosti kvadrantu, v ktorom leží vypočítaný uhol a problému nerovnomernej presnosti je použitie dvojosového akcelerometra. Pri použití takéhoto akcelerometra sa gravitačné zrýchlenie rozkladá na dve zložky (dve priemety, ktorých výslednicou je gravitačné zrýchlenie). Jedna os je paralelná so smerom gravitácie a druhá os je na ňu kolmá, za predpokladu nulového uhla θ. Pri vychýlení o uhol θ výstupmi akcelerometra budú sínusové a kosínusové priemety gravitačného zrýchlenia.

Uhol natočenia sa teda dá vypočítať buď zo sínusového priemetu alebo z kosínusového priemetu ,čo je veľkou výhodou, lebo sa na výpočet dá použiť funkcia tangens . Podiel oboch priemetov zabezpečuje konštantnú presnosť počas celej rotácie okolo 360°. Senzor je najcitlivejší pri zmenách zrýchlenia ak je kolmý na gravitačnú silu a naopak najmenej citlivý pri paralelnosti s ňou. Keďže funkcie sínus a kosínus sú navzájom posunuté práve o 90°, v momente keď je najcitlivejšia sínusová zložka, kosínusová je naopak najmenej. Tým, že počítaný uhol je daný podielom týchto funkcií zabezpečuje sa spomínaná rovnaká presnosť počas celého priebehu.

Ak ide o trojosí akcelerometer gravitačné zrýchlenie sa takto rozkladá do troch osí. Keďže ide o osi ortogonálnej sústavy, sú to tri navzájom kolmé vektory, ktorých vektorový súčet je práve spomínané gravitačné zrýchlenie. Smer zrýchlenia je samozrejme rovnobežný so zvislicou a veľkostne sa rovná 1g. Ak je teda ľubovoľná os rovnobežná so zvislicou, gravitačné zrýchlenie je premietnuté iba do tejto osi a údaje z ďalších osi sú nulové. Ako náhle vychýlime akcelerometer, zrýchlenie sa rozloží aj do ostatných osí. Z týchto troch údajov vieme zistiť uhly vychýlenia od jednotlivých osí (od osi x uhol ρ (pitch), od osi y φ(roll) a od zvislice θ).

Základným poznatkom je teda rovnosť v statickom stave . Vynechaním bodov v ktorých funkcia tangens nie je definovaná vieme pre dané uhly napísať vzťahy:

	(1.0)

Keďže tangens je periodická nepárna funkcia s periódou π je potrebné zistiť v ktorom kvadrante sa vypočítaný uhol naozaj nachádza. Za príklad zoberme určenie uhla náklonu od osi x, teda ρ. Ak bude údaj A_x kladný môžeme s istotou tvrdiť, že uhol ρ je z I. alebo z II. kvadrantu, ak je A_x záporný tak uhol je z III. alebo IV. kvadrantu. O konečnom zaradení uhla do kvadrantu rozhodne znamienko údaja A_z.

Ak rozhodujeme medzi I. alebo II. kvadrantom (A_x>0) A_z je kladné pre I. kvadrant a záporné pre II. kvadrant. Ak sa rozhodujeme medzi III. a IV. kvadrantom (A_x<0) A_z je kladné pre IV. kvadrant a záporné pre III. kvadrant. Samozrejme arcustangens má obor hodnôt (-π/2;π/2), takže uhly v II., III. a IV. treba prepočítať.

I. kvadrant :ρ=ρvyp.
II. kvadrant :ρ=180 -|ρvyp.|
III. kvadrant :ρ=180 +|ρvyp.|
IV. kvadrant :ρ=360 -|ρvyp.|

Analogicky platia vzťahy aj pre výpočet uhlov φ a θ.

Zisťovanie uhlov náklonu je nesmierne dôležité z hľadiska okamžitého určenia polohy akcelerometra počas kmitania. Keďže pri zmene polohy je potrebný údaj o začiatočnej polohe, najjednoduchšie riešenie je poznať hodnoty inicializačných uhlov, čo znamená poznať uloženie akcelerometra na bremene. Je však nutné zamyslieť sa nad tým, či je zo signálu možné okamžité uhly náklonu získať.

Kompenzácia tangenciálnej zložky zrýchlenia

Ak máme teda informáciu o počiatočnej polohe snímača ( položme uhly ρ φ θ za nulové a tak isto uhol okolo zvislice za nulový) môžeme zahájiť meranie. Pre zjednodušenie predpokladajme že budeme merať výchylku v rovine xz a takže pri meraní budeme očakávať nulovú hodnotu zložky A_y . Výstup snímača nám teraz bude poskytovať dve informácie, t.j. rozklad gravitačného zrýchlenia do zložky A_x a do zložky A_z. Mali by to mali byť násobky sínusovej resp. kosínusovej funkcie uhla vychýlenia α a gravitačného zrýchlenia.

No tento opis samozrejme nie je úplný, nie je v ňom zahrnutá žiadna dynamika. To potvrdilo aj meranie, ktorým sa zistilo, že jedna zo zložiek (teda očakávaná sínusoida) je nulová. Na druhej strane pri očakávanom kosínusovom priebehu zložky A_z sa na výstupe objavil nasuperponovaný signál. Príčinou tohto výsledku je rozdelenie zrýchlenia matematického kyvadla , ktorého zložky sú interpretované ako tangenciálne a odstredivé zrýchlenie.

Tangenciálne zrýchlenie pôsobí na tangenciálnu zložku gravitačného zrýchlenia (ich vektory sú rovnobežné) a odstredivé zrýchlenie pri pohybe kyvadla pôsobí (sčítava sa) na radiálnu zložku gravitačného zrýchlenia (smer závesu), pričom má tiež smernicu rovnobežnú s odstredivým zrýchlením. Rovnaký smer jednotlivých zložiek umožňuje tieto hodnoty jednoducho sčítať.

Vynulovanie tangenciálnej zložky si môžeme predstaviť ako voľný pád, pri ktorom samozrejme tiež nič nenameráme. Touto úvahou vieme konštatovať, že tangenciálnu zložku (teda jeden výstupný údaj akcelerometra) nijako nezískame. Druhý výstupný údaj samozrejme nulový nie je, no je na ňom okrem kosínusového priemetu gravitačného zrýchlenia nasuperponovaná hodnota odstredivého zrýchlenia, čo nie je príliš vhodné pre určenie aktuálnej výchylky. Pri matematickom opise jasne uvidíme prečo.

Matematický opis pohybu matematického kyvadla

Priebeh uhla pri pohybe kyvadla vieme opísať rovnicou

(1.1)

Pre uhlovú rýchlosť platí vzťah

(1.2)

Pre uhlové zrýchlenie platí vzťah

(1.3)

Pre tangenciálne zrýchlenie platí vzťah

(1.4)

Pri uvažovaní matematického kyvadla pre malé výchylky (do 5°) platí

(1.5)

Po dosadení rovnice (1.5) do (1.4) dostávame vzťah pre tangenciálne zrýchlenie v tvare

(1.6)

Pre odstredivé zrýchlenie platí vzťah

(1.7)

Po dosadení rovnice (1.5) do (1.7) dostávame pre odstredívé zrýchlenie vzťah

(1.8)

Vzťahy (1.6) a (1.8) sú pre nás najdôležitejšie, lebo práve tangenciálne a odstedivé zrýchlenie nám bude ovplyvňovať meranie. Ako bolo spomenuté akcelerometer nám bude merať zložky gravitačného zrýchlenia v závislosti od vychýlenia bremena, na ktorom je upevnený. Tangenciálna zložka meraná akcelerometrom

(1.9)

Po dosadení rovnice (1.1) do rovnice (1.9) dostávame vzťah

(2.0)

Pri predpokladaných malých výchylkach (do 5°) platí sin⁡(x) je približne x, potom sa rovnica (2.0) zjednoduší na tvar

(2.1)

Takisto úpravou a dosadením rovnice (1.1) dostávame vyjadrenie radiálnej zložky gravitačného zrýchlenia meraného akcelerometrom

(2.2)

Ak máme teda vyjadrené gravitačné zložky a takisto jednotlivé zrýchlenia, môžeme ich vďaka rovnakému smeru jednoducho sčítať (po tangenciálnych a radiálnych zložkách). Dostaneme tak vzťahy, ktoré nám budú opisovať výstupné údaje akcelerometra v závislosti od meniacej sa polohy bremena.

(2.3)

(2.4)

Ako vidno z rovnice (2.3), jeden z výstupných údajov sa bude rovnať nule ako sme predpokladali. Druhý údaj bude zložený z dvoch zložiek t.j. zo zložky potrebnej na meranie, no aj zo zložky odstredivého zrýchlenia, ktorá toto meranie značne znehodnotí. Ideálnym prípadom by bolo možnosť odstrániť toto zrýchlenie z meraného signálu. Pokusy o odstránenie zrýchlenia však neboli úspešné. Je však zaujímavé všimnúť si párnosť periodických funkcií použitých v rovnici (2.4) a zamyslieť sa nad zmyslom odstránenia tohto nasuperponovaného zrýchlenia. Aj keby sa nám podarilo odstrániť odstredivú zložku, stále by bol k dispozícii iba signál s kosínusovým priebehom.(párna funkcia !!)

Teoreticky je možné zisťovať okamžitú polohu bremena aj z informácie obsahujúcej odstredivé zrýchlenie a to riešením rovnice (2.4). Neznámu nám pritom predstavuje argument goniometrických funkcií (okamžitý uhol vychýlenia). Ak sa však pozrieme na použité goniometrické funkcie, ľahko môžeme povedať, že síce vieme zistiť veľkosť vychýlenia, ale nikdy jeho smer (čiže znamienko) kvôli párnosti týchto funkcií.

Môžeme akokoľvek natáčať merací prístroj, potrebná tangenciálna zložka opísaná nepárnou funkciou sinus je stále kompenzovaná. Smer vychýlenia by sa dal merať iným meračom, a tak zabezpečiť úplnú informáciu o polohe bremena. Akcelerometer sa však dá využiť aj inak, a to na meranie frekvencie kmitov, čo pri návrhu algoritmov riadenia jeho kľúčovou úlohou.

Meranie frekvencie pomocou akcelerometra

Meranie frekvencie pohybu kyvadla s akceptovateľnou presnosťou je jedným z hlavných krokov pri návrhu správne fungujúcich algoritmov určených na utlmenie kmitavého pohybu. Existuje viacero prístupov k danej problematike, pričom každý obsahuje viacero metód so špecifickými vlastnosťami, kde pri výbere metódy záleží na konkrétnej aplikácii s vopred určenými hodnotami presnosti prípadne rýchlosti výpočtu.

K jedným z najjednoduchších prístupov patrí určovanie frekvencie priamo zo signálu. Problémom je však skutočnosť, že frekvencia potrebná pre návrh algoritmov musí byť nevyhnutne meraná z oscilácii pri minimálnych uhloch vychýlenia bremena. To naznačuje, že signál bude silne zašumený a uvedená metóda prechodu signálu cez jeho strednú hodnotu bude nepoužiteľná, kvôli nejednoznačnosti určenia prechodu. Ponúka sa teda možnosť analyzovať tento silne zašumený signál vo frekvenčnej oblasti, teda využiť diskrétnu Fourierovu transformáciu, využiť štatistické funkcie autokorelácie a poznatky z analýzy stochastických signálov diskrétnych v čase.

Spektrálna analýza diskrétneho signálu akcelerometra

Prechod z časovej oblasti do frekvenčnej oblasti pomocou diskrétnej Fourierovej transformácie, prípadne jej zrýchlených algoritmov výpočtu, patrí k najvýznamnejším postupom číslicového spracovania signálov. Využitím ortogonálnosti trigonometrického systému je možné opísať akýkoľvek signál vyskytujúci sa v praxi. Pomocou konečných radov (pri diskrétnych signáloch) trigonometrických funkcii je možné získať z daných vzoriek obmedzeného časového priebehu potrebné vzorky spektra, prípadne opačne. Váhové koeficienty jednotlivých zložiek transformácie reprezentujú spektrum signálu, či už amplitúdové (absolútna hodnota), alebo fázové (argument).

Jednotlivé vzorky (odpovedajúce presne známym časovým okamihom) sú od seba najčastejšie vzdialené o rovnaký časový interval T (pri rovnomernom vzorkovaní). Získané diskrétne vzorky x(nT) sú konečnou diskrétnou postupnosťou (s dĺžkou N) vhodnou na diskrétnu Furierovu transformáciu.

k=0,1,..,N-1
n = 0,1,..,N-1	(2.5)

Teda každá nenulová hodnota Fourierovej transformácie (2.5) reprezentujúca istú frekvenciu trigonometrických funkcií, naznačuje výskyt danej frekvencie v rade frekvencií, z ktorých je zložený signál. Dôležitá je voľba počtu vzoriek N, respektíve počet periód signálu nachádzajúcich sa v jednom bloku údajov s dĺžkou N. Keďže dopredu nie je známe koľko periód signálu sa nachádza v skúmanom časovom intervale navzorkovanom s určitou periódou vzorkovania, nie je získaný obraz spektra úplne presný.

Ak sa v tomto intervale nachádza viac periód (dôležité je pritom, aby to bol celočíselný násobok) výsledok je rovnako presný ako pri jednej perióde, len je potrebné zväčšiť periódu vzorkovania. Keďže sa predpokladá, že signál je periodický na celom svojom priebehu (nielen na vybranej časti s N vzorkami) logicky aj jeho spektrum by malo byť periodické. Spektrum diskrétneho periodického signálu je periodiské s periódou N.

Fourierov rad funkcie opisujúcej priebeh signálu na určitom úseku je tým istým Fourierovým radom takzvaného periodického predĺženia tejto funkcie. Periodickým predĺžením časti signálu dĺžky N je samotný celý priebeh signálu. To len potvrdzuje, že akákoľvek časť takéhoto periodického signálu (zvolená časť musí však obsahovať minimálne jednu periódu ) bude mať rovnaké spektrum. V prípade, že vybraný úsek obsahuje neceločíselný násobok periódy signálu neexistujú presné hodnoty špičiek v spektre odpovedajúce jednotlivým harmonickým zložkám, sú posunuté a nereprezentujú presne harmonické zložky ako pri celočíselných násobkoch (hlavne pri malých neceločíselných násobkoch).

Predtým ako bude naznačený postup odstránenia tejto chyby je dôležité pozastaviť sa nad korektnou interpretáciou spektra. Ako bolo naznačené, každá hodnota k reprezentuje istú frekvenciu spektra, pričom hodnoty týchto frekvencií sa pohybujú medzi hodnotami 〈0 ; (N-1)/NT〉 podľa vzťahu f_k=k/NT pre k=0,1,2,…,N-1. Problém nastáva vtedy ak k nadobudne hodnotu N/2. To je hraničným prípadom splnenia Shanon-Kotelnikovej teorémy, frekvencia totiž nadobúda polovičnú hodnotu vzorkovacej frekvencie. Z toho vyplýva, že pri spektrálnej analýze signálu sú reprezentatívne len zložky do hodnoty k=N/2.

Rozmazávanie spektra

Ako bolo spomenuté, presnosť zistenia harmonických zložiek signálu zo spektra závisí od počtu periód resp. od celočíselného alebo neceločíselného násobku periódy v analyzovanej časti signálu s dĺžkou N. Ak navzorkovaná časť obsahuje p periód, perióda spektra sa zväčší p-krát (pri nezmenenej vzorkovacej frekvencii), keďže dĺžka časového intervalu je tiež p-krát dlhšia. Spektrum si však zachová pôvodný tvar, zmení sa len vzdialenosť jednotlivých bodov mriežky určujúcich jednotlivé harmonické zložky (sú m-krát bližšie, keďže je ich m-krát viac). Ak však nejde o koherentne navzorkovaný signál prejaví sa deformovanie spektra, takzvané presakovanie energie do susedných frekvenčných bodov (ang. leakage).

Metóda, ktorá je schopná čiastočne potlačiť túto chybu a získať tak tvar spektra podobnejšiu tomu skutočnému sa nazýva metóda váhovania signálu oknom. Jednoducho povedané ide o vynásobenie navzorkovanej časti signálu s dĺžkou N takzvanou oknovou funkciou w(n). Oknová funkcia má rovnakú dĺžku ako vybraná časť signálu, je osovo súmerná podľa y-ovej osi, prechádzajúcej stredom okna a monotónne klesá k obom koncom limitne k nule. Maximálna hodnota, ktorú táto funkcia vo svojom priebehu dosahuje sa rovná jednej a dosahuje ju vo svojom strede. Príklad priebehu oknovej funkcie je na obrázku č. 2. (Hann).

Obr.2:Priebeh Hannovej oknovej funkcie

Najdôležitejšie vlastnosti oknovej funkcie vychádzajú z jej spektrálneho obrazu. Patria k ním šírka hlavného oblúku, výška prvého postranného oblúku a rýchlosť poklesu postranných oblúkov. Ide o vlastnosti, podľa ktorých sa vhodne vyberajú rôzne typy okien pre potrebnú úpravu skúmaného spektra signálu. V literatúre sa však uvádza, že pri signáli s nasuperponovaným širokopásmovým šumom na výbere typu okna výrazne nezáleží.

Dôležité je však, že pri splnení podmienky koherentného vzorkovania (NT_vz = MT_s N-počet vzoriek, T_vz- vzorkovací interval, M_- počet periód, T_s- doba periódy signálu.) sa okno nesmie použiť, keďže spektrum obsahuje spektrálne čiary priamo zodpovedajúce harmonickým zložkám. V prípade použitia by spektrum obsahovalo aj kratšie postranné spektrálne čiary súmerne rozložené okolo spektrálnej čiary presne reprezentujúcej harmonickú zložku.

Signál upravený oknovou funkciou je možné vyjadriť x_w=x(n)*w(n), prípadne rovnicou vo frekvenčnej oblasti v tvare X_w (θ)=X(θ)*W(θ). Okná môžu byť symetricky umiestnené okolo začiatku časovej osi, no pri analýze signálu senzora je okno zvyčajne umiestnené na začiatku časovej osi, ako je to pri aplikáciách na signály bežné. Podľa spomínaných vlastností existuje veľké množstvo typov okien, každé s vlastnými špecifikami podľa potreby použitia.

Či už pri spektrálne analýze alebo pri návrhu číslicovej filtrácii sa používajú sa aj nasledujúce okná: Pravouhlé, Bartlettovo, Backmanovo, Chebyshevovo, Hammingovo, Kaiserovo, či trojuholníkové. Pravouhlé okno sa napríkad používa iba na výber určitej časti signálu. Backmanovo okno má zas oproti Hannovmu resp. Hammingovmu širší hlavný oblúk a nižšie postranné onlúky.

Kaiserovo okno zas obsahuje parameter, ktorým sa dá meniť šírka hlavného oblúka a tak isto výška postranných oblúkov. Použitím spomínaných okien je možné priblížiť sa reprezentatívnejšiemu tvaru spektra signálu akcelerometra, a tak presnejšie určiť harmonické zložky, z ktorých je periodický signál zložený. Na obrázku č.3 je znázornený vplyv oknových funkcií na signálové spektrum.

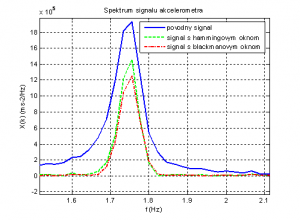
Obr.3: Vplyv oknových funkcií na spektrum signálu

Pri vysokom zašumení sa však nedajú využiť metódy vychádzajúce z odčítania maximálnych hodnôt prislúchajúcich frekvenčných zložiek spektrálneho obrazu signálu. Frekvenčný obraz buď nevykazuje žiadne prevládajúce hodnoty, alebo je týchto lokálnych maxím priveľa. Načrtá sa teda možnosť využiť štatistické metódy spracovania signálu ako aj stochastický pohľad na zašumený signál.

Stochastický pohľad na silne zašumený signál a jeho analýza

Stochastický (náhodný) signál je signál, ktorého hodnoty sú generované náhodne a jeho hodnoty sa nedajú predpovedať do budúcna. Keďže pri meraní kmitov je na harmonickom priebehu signálu nasuperponovaný šum, je možné daný signál pokladať za náhodný. Zaoberať sa analýzou náhodnej veličiny znamená mať pre určitý čas vzorky (jednotlivé rezy v čase) z takzvaných realizácii náhodného signálu. Pre daný čas rezu je teda k dispozícii n počet vzoriek (n je počet realizácii náhodného signálu), z ktorých je možné vyhodnocovať základné vlastnosti náhodnej veličiny.

Podľa toho či sú základné štatistické charakteristiky (stredná hodnota, rozptyl) nezávislé na čase, čiže rovnaké v ľubovoľných rezoch daných realizácii, sa delia na procesy stacionárne a procesy nestacionárne. V praxi je však k dispozícii konečný úsek jednej realizácie náhodného signálu. Keďže pre signál je splnený predpoklad stacionárneho procesu, je z tohto meraného úseku pomocou štatistických charakteristík možné získať rôzne parametre, napríklad hľadanú frekvenciu.

Pri opise signálu v časovej oblasti je jednou z najdôležitejších a pre ďalší výpočet potrebných charakteristík stredná hodnota. Z nej totiž priamo vychádza definícia korelačnej resp. autokorelačnej postupnosti. Autokorelačná postupnosť vyjadruje súvislosť medzi jednotlivými rezmi signálu (v tomto prípade vzorkami jedinej realizácie). Ak je signál stacionárny stredná hodnota nie je závislá od času. Autokorelačná funkcia teda nie je funkciou času, ale časového posunu p= n – m. Autokorelačná funkcia je definovaná aj pre záporné hodnoty p (je simetrická).

Dôležitejšou je však skutočnosť, že ak signál obsahuje harmonickú zložku, obsahuje ju aj autokorelačná funkcia. Ak signál obsahuje viac harmonických zložiek, z periódy autokorelačnej funkcie sa nedajú priamo určiť jednotlivé frekvenčné zložky. To však neplatí o signále s jedinou harmonickou zložkou. Veľkou výhodou určovania frekvencie z autokorelačnej funkcie je jej relatívne hladký priebeh, čiže aj jednoznačnejší prechod strednou hodnotou potrebný na meranie periódy (narozdiel od zašumeného signálu, pri ktorom sa na metódu prechodu strednou hodnotou nedalo spoľahnúť).

Zaujímavá je skutočnosť, že autokorelačná funkcia je takmer zhodná aj pre signál s nasuperponovaným bielym šumom, ktorým je, predpokladajme, zašumený aj reálny signál. Periódu harmonickej zložky je potom potrebné určovať v dostatočnom časovom oneskorení (τ→∞),kde sa táto ustáli na určitú hodnotu pri nulovej strednej hodnote signálu. Keďže stredná hodnota bieleho šumu je nulová, nemá tak plyv na autokorelačnú funkciu. Priame určovanie frekvencie z priebehu autokorelačnej funkcie je však náchylné na šum, ktrorý vykazuje náznaky periodicity.

Na formuláciu ďalších metód využívajúcich stochastický prístup je potrebné definovať výkonovú spektrálnu hustotu signálu. Je definovaná Fourierovou trasformáciou autokorelačnej funkcie. Výkonovú spektrálnu hustotu si je možné predstaviť ako funkciu, po integrovaní ktorej dostávame informáciu o výkone vybranej časti signálu. (vybranou časť signálu sa myslí vybraný frekvenčný interval). Ak je teda na vymedzenom intervale frekvencií značne odlíšiteľný výkon v porovnaní od iných frekvenčných intervalov, je daná frekvencia v signáli prevládajúca.

Frekvenčný interval je určený hranicami integrácie, resp. sumácie. Na výpočet odhadu výkonovej spektrálnej hustoty existuje mnoho metód. Podľa požiadaviek kladených na presnosť určenia a charakter meraného signálu sa dajú rozdeliť do viacerých kategórii

1. Bezparametrické metódy
2. Parametrické metódy
3. Metódy vysokého rozlíšenia

Bezparametrické metódy

Bezparametrickými metódami je odhad výkonovej spektrálnej hustoty určovaný priamo zo signálu, a to ako druhá mocnina Fourierovej transformácie podelený súčinom dĺžky signálu a periódou 2π resp. frekvenciou vzorkovania ak je výkonové spektrum vyjadrené pomocou frekvencie. Táto metóda nezohľadňuje vyššie popísané chyby spôsobené presakovaním energie, chyby nekoherentného vzorkovania, preto je pomerne nepresná (obdoba amplitúdového spektra).

Modifikáciou metódy vychádzajúcej z priameho určovania výkonovej spektrálnej hustoty je Welchova metóda. Táto metóda zohľadňuje nekoherentné vzorkovanie použitím okien. Základným predpokladom je rozdelenie signálu na viacero úsekov. Na každý segment sa aplikuje okno (Hann, Hamming,…), pričom okno má rovnakú dĺžku ako segment. Susedné segmenty sa navzájom prekrývajú, pričom sa určí na koľko percent sa majú prekryť. Literatúra uvádza za najviac používanú hodnotu 50%.

Vzniká tak sieť navzájom prekrytých okien, ktorých začiatok je v časti predchádzajúceho okna. Percentuálny výber závisí od použitých okien, keďže každé okno má špecifický tvar, t.j. rôznu šírku hlavného laloka, ako aj šírku vedľajších lalokov. Počet segmentov teda závisí na dĺžke skúmaného signálu, počte prekrytých vzoriek a šírke segmentu. Literatúra uvádza za najpoužívanejší počet 8 segmentov. Na každú časť takto rozdeleného signálu sa aplikuje Fourierova transformácia a vypočíta sa z nej priemerná hodnota kvadrátu amplitúdového spektra .

Na zvýšenie presnosti určenia sa jednotlivé kvadráty spriemerujú. Tak ako bol korigovaný výpočet frekvencie pri interpolácii Fourierovej transformácie v dôsledku použitia okien, aj v tomto prípade je nutné zohľadniť túto skutočnosť. Výpočítané spectrum sa tak musí vydeliť sumou kvadrátov hodnôt použitého okna. Je samozrejme jedno, či videlíme každý segment zvlášť, alebo výsledný priemer, kedže je zásadne použitý len jeden typ okna. Výsledné spektrum je intuitívne periodické s periódou 2π resp. fvz.Na obrázku č. 4 je zobrazené výkonová spektrálna hustota pomocou Welchovej metódy.

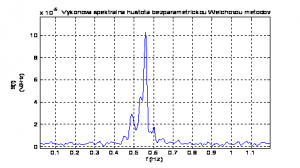
Obr.4: Výkonová spektrálna hustota signálu bezparametrickou Welchovou metódou

Ako možno pozorovať z obrázku č. 4, táto metóda je výraznejšie presnejšia, keďže nezanedbáva chyby vznikajúce pri Fourierovej transformácii. Možno však poznamenať, že ak je na signáli nasuperponovaný šum, ktorý obsahuje krátke impulzy (napríklad vplyv prostredia ) presnosť tejto metódy potom závisí od toho, v akom mieste skúmaného signálu sa impulz objavil. Kvôli rozloženiu oknových funkcií teda nemožno povedať, že ak sa vzruch objaví v hlavnom laloku oknovej funkcie spôsobí rovnakú zmenu výsledného spektra, akú by spôsobil v postranných lalokoch okna.

Je preto dôležité zvoliť vhodný tvar okna ako aj vhodné percentuálne prekrytie segmentov. Tak isto si treba uvedomiť, že použitím prílišného prekrývania vzoriek oknovými funkciami (dajú sa interpretovať aj ako dolnopriepustné filtre) sa síce zníži variancia odhadu výkonového spektra, ale kvalita rozlíšenia klesá. To nie je žiaduce v prípadoch, ak sa v spektre nachádzajú dve frekvenčné zložky tesne vedľa seba. Parametrické metódy a metódy vysokého rozlíšenia sú výpočtovo náročnejšie a nebudeme sa im detailnejšie venovať.

Záver

Po analyzovaní správania sa MEMS akcelerometra pri kmitavom pohybe, možno konštatovať, že nie je vhodný na dynamické meranie aktuálnej výchylky bremena voči zvislici, keďže výstupný signál má kosínusový priebeh. Akcelerometer však možno využiť pri meraní frekvencie kmitov bremena, pričom získaná frekvencia je dvojnásobkom reálneho kmitania. Výberom vhodnej metódy je možné akcelerometrom merať aj silne zašumený signál. Ako najpresnejšia sa javila Welchova metóda využívajúca Fourierovu transformáciu doplnenú oknovou funkciou a štatistické spracovanie signálu. Presne odmeraná perióda kmitov má svoj význam pri návrhu algoritmov utlmujúcich vlastné kmity bremena.

Použitá literatúra

1. Sedláček, M., Šmíd, R.: Matlab v Měření, Vydavatelství ČVUT, Praha, 2003
2. Kotuliakova, J., Rozinaj, G.: Číslicové spracovanie signálov, Vydavateľstvo STU, Bratislava, 2001
3. Ondráček, O.: Signály a sústavy, SVŠT, Bratislava, 1991
4. Tuck, K. 2007. Tilt Sensing Using Linear Accelerometers. [online]. 2007. Dostupné na internete <http://cache.freescale.com/files/sensors/doc/app_note/AN3461.pdf>

---

Spoluautorom článku je doc. Ing. Peter Hubinský, PhD., ÚRPI FEI STU